Focus Question: What is magnetic flux?
- Magnetic Flux – φ, Amount of magnetic field that goes through a surface.
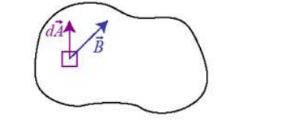
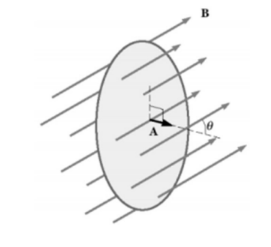
$\phi=\int \vec{B} \cdot \overrightarrow{d A}=B A \cos \theta$
Units: 1 weber $(\mathrm{Wb})=1 \mathrm{Tm}^2$
*Field vs. flux $-d \phi=B_{\perp} d A \rightarrow B_{\perp}=\frac{d \phi}{d A}$. The magnetic field equals the flux per unit area, so the magnetic field is sometimes called “flux density”.
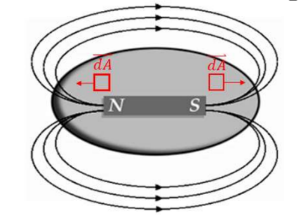
- Gauss’s Law for Magnetism concerns magnetic flux through a closed surface:
$
\phi=\int \vec{B} \cdot \overrightarrow{d A}=0
$
The total magnetic flux through a closed surface is zero.
Gauss’s Law for Magnetism is true since there are no magnetic monopoles.
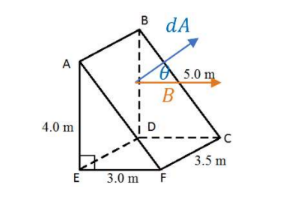
Example A: A uniform magnetic field $|B|=0.80 \mathrm{~T}$ acts in the positive y-direction.
a) Calculate the flux through surface ABDE.
b) Calculate the flux through surface ABCF.
Answer/Explanation
a) The flux and dA are in opposite directions since the flux to in the $+\mathrm{y}$ to the right, and $\mathrm{dA}$ is out of the surface, which is to the left:
$
\phi=B A \cos 180^{\circ}=-(.8 \mathrm{~T})(3.5 \mathrm{~m})(4 \mathrm{~m})=-11.2 \mathrm{~Wb}
$
b) dA points directly out of the surface as shown. The field is in the positive y- direction:
$\phi=B A \cos \theta=(.8 T)\left((3.5 m)(5 m) \frac{3}{5}=8.4 \mathrm{~Wb}\right.$
Example B: A uniform $2.0 \mathrm{~T}$ magnetic field passes through a circular loop with a radius of $0.2 \mathrm{~m}$ that has 4 turns. Calculate the flux through the loop.
Answer/Explanation
$
\phi=B A=(2 T)\left(\pi(.2 m)^2\right) x 4=1 \mathrm{~Wb}
$
Example C: An infinitely long conducting wire carries a current of I and is a distance of $a$ from a rectangular surface as shown. Derive an expression for the magnetic flux through the rectangle.
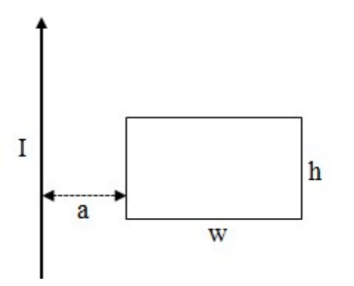
Answer/Explanation
The field is not constant through the loop, so it is broken into many dA’s along its length in the x-direction since field varies in $\mathrm{x}$. Each dA has a thickness of $d x$ and an area of hdx. .
The field in each dA is constant vertically and is equal to $\frac{\mu_0 I}{2 \pi r}$, where $\mathrm{r}$ is the distance to the wire.
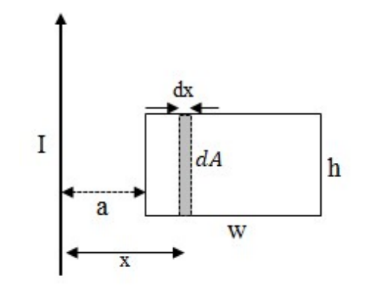
$\begin{aligned} & \phi=\int B \cdot d A=\int_a^{a+w} \frac{\mu_0 I}{2 \pi x} h d x=\frac{\mu_0 I h}{2 \pi} \int_a^{a+w} \frac{d x}{x} \\ & \rightarrow \frac{\mu_o I h}{2 \pi} \ln |x|^{a+w}=\frac{\mu_0 I h}{2 \pi}(\ln |a+w|-\ln |a|) \\ & \boldsymbol{\phi}=\frac{\boldsymbol{\mu}_0 \boldsymbol{I} \boldsymbol{h}}{\mathbf{2 \pi}} \ln \left|\frac{\boldsymbol{a}+\boldsymbol{w}}{\boldsymbol{a}}\right|\end{aligned}$
Focus Question: What causes an induced emf?
- When the magnetic field through a loop of wire changes, a current is induced in the loop of wire. In the diagram below, the electrons in the wire experience a force, and the resulting movement induces current in the wire, even though the wire is not connected to a power source.
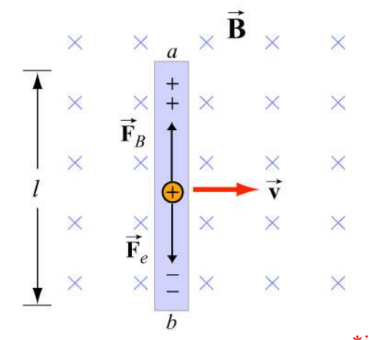
When the bar is moved to the right in a field that outs into the page as shown, positive charge is pushed up by the right-hand rule. Since there is current in the wire, there must be a potential difference. Charge accumulates until the electric force caused by the potential difference cancels out the magnetic force:
$
\begin{gathered}
F_B=F_E \\
q B v=E q \rightarrow B v=\frac{\varepsilon}{l} \\
\rightarrow \boldsymbol{\varepsilon}=\boldsymbol{B v} \boldsymbol{l}
\end{gathered}
$
*induced emf in a bar of length moving at speed in a magnetic field of B
If the bar is part of a completed circuit loop as shown, then the moving bar acts as a battery due to the induced emf in the bar.
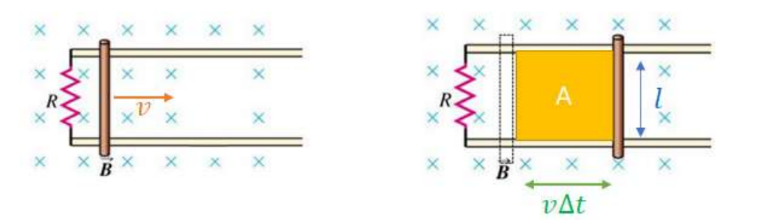
As the bar moves to the right, it covers an area of A as shown in a time ∆t.
$
\phi=B A=B v \Delta t l
$
The time rate of change of the flux is $\frac{\phi}{t}=B v l$ since velocity is constant. This is equal to the emf.
Example A: A bar of lenth $.20 \mathrm{~m}$ is moved to the right at a speed of $\mathrm{v}=4.0 \mathrm{~m} / \mathrm{s}$ in a field of magntidue $\mathrm{B}=2.0 \mathrm{~T}$ as shown. The resistor has a value of $R=2.0 \Omega$.
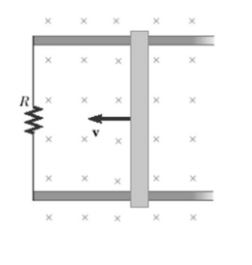
a) Find the current in the circuit.
b) Calculate the force required to keep the rod moving.
a) $I=\frac{\varepsilon}{R}=\frac{B l v}{R}=\frac{(2 T)(.2 \mathrm{~m})\left(4 \frac{\mathrm{m}}{\mathrm{s}}\right)}{2 \Omega}=0.8 \mathrm{~A}$
b) $F=B I L=(2 T)(.8 A)(.2 m)=.32 T$
- Faraday’s Law with Calculus – The induced emf due to a changing magnetic field is equal to the rate of change of the magnetic flux through the surface bounding by the circuit:
$\begin{gathered}\varepsilon=\frac{-d \phi}{d t} \\ \varepsilon=\frac{-d}{d t} \int \vec{B} \cdot \overrightarrow{d A} \cos \theta\end{gathered}$
*The minus sign indicates the magnetic force produced by the induced current opposes the force that causes it.
- Ways to change flux:
- Change the magnitude of the magnitude.
- o Change the size of the area the flux is passing through.
- o Change the angle made by the field and the surface it passes through.
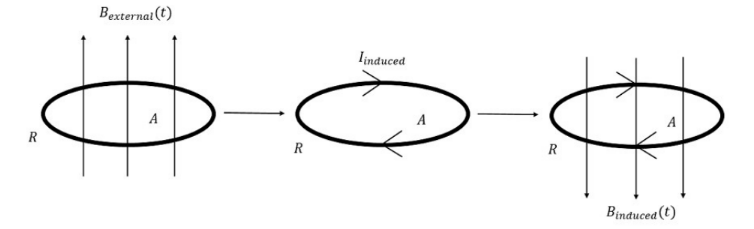
- Lenz’s Law
“An induced current will have a direction such that it will oppose the change in flux that produced it.” (the minus sign in Faraday’s law)
Example B: Determine the direction of the current in the wire in each of the cases below:
a) B is increasing b) B is increasing c) B is decreasing
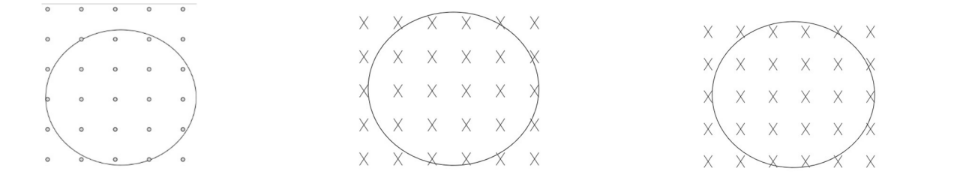
Answer/Explanation
a) The field is out of the page and increasing, so the change in flux is out of the page. The induced current resists the change in flux by inducing a current that creates a field into the page to oppose the change in flux, so the current is clockwise.
b) The field is into the page and increase, so the change in flux is into the page. The induced current creates a field out of the page to oppose the direction of the change in flux, so the current is counter-clockwise.
c) The field is into the page and decreasing, meaning the change in flux is out of the page. he induced current resists the change in flux by inducing a current that creates a field into the page to oppose the change in flux, so the current is clockwise.
Example C: A magnetic field has a strength given by $B(t)=2 t^2-2 t+2$ and acts out of the plane of this page. A circular loop of wire of radius $\mathrm{R}=2.0 \mathrm{~m}$ within the plane of this page has the field pass through it.
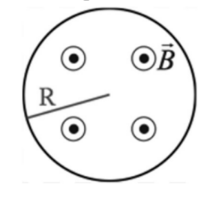
a) Find the induced emf in this wire as a function of time.
b) Find the direction of the current in the wire at t = 2.0 s.
Answer/Explanation
(a) $\varepsilon=-\frac{d \phi}{d t}=-A \frac{d B}{d t}(\mathrm{~A}$ is constant and $\mathrm{B}$ changes with $\mathrm{t})$
$
\begin{aligned}
& \rightarrow \varepsilon=-(\pi)(2)^2(4 t-2) \\
& \rightarrow \varepsilon(t)=16 \pi t^2-8 \pi
\end{aligned}
$
(b) At $\mathrm{t}=2, \frac{d b}{d t}=4(2)-2=6$. B is increasing since $\mathrm{dB} / \mathrm{dt}$ is positive. Thus the flux is increasing out of the page, so the change in flux is out of the page. The induced current creates a field into the page to the induced current is clockwise.
- Flux Linkage
For a coil of wire with many loops:
An emf is induced in each loop of wire, more loops $=$ more emf
$
\varepsilon=\frac{-N \Delta \Phi}{\Delta t}
$
*Each loop produces its own emf, and the emfs from each loop add to the total emf.
Example D: A metal wire coil of radius $0.5 \mathrm{~m}$ has 1000 loops, forming a solenoid. The solenoid is placed in a $500 \mathrm{mT}$ magnetic field. The field drops to $0 \mathrm{~T}$ in $10 \mathrm{~s}$. What is the induced emf in the coil?
Answer/Explanation
$
\varepsilon=-\frac{N d \phi}{d t}=-N A \frac{d B}{d t}=-(1000)(\pi)(0.5 \mathrm{~m})^2 \frac{0-\left(500 \times 10^{-3} \mathrm{~T}\right)}{10 \mathrm{~s}}=\frac{25 \pi}{2} \mathrm{~V}
$
Example E: A square loop $(\mathrm{s}=0.25 \mathrm{~m})$ is placed around a solenoid of 1000 loops with a diameter of $.10 \mathrm{~m}$ and length of $0.2 \mathrm{~m}$. The loop’s plane is perpendicular to the axis of the solenoid. The current in the Solenoid is given by $I=100\left(1-e^{-\frac{t}{5}}\right)$. Calculate the induced emf in the loop as a function of time.
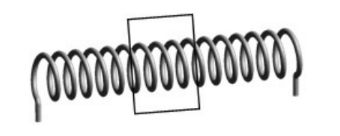
Answer/Explanation
Using the field of a solenoid derived in 10.4: $\phi=B A=\frac{\mu_0 N I(t)}{L} \pi r^2$
$
\begin{aligned}
& \rightarrow B=\frac{\mu_0 N \pi r^2}{L} 100\left(1-e^{-\frac{t}{5}}\right) \\
& \varepsilon=-\frac{d B}{d t}=s^2 \frac{\mu_0 N \pi r^2}{L} 20 e^{-\frac{t}{5}}=(.25 m)^2 \frac{\left(4 \pi x 10^{-7} \frac{T m}{A}\right)(1000) \pi(.05 m)^2}{.2 m}(20) e^{-\frac{t}{5}} \\
& \rightarrow \varepsilon=.001 e^{-\frac{t}{5}}
\end{aligned}
$
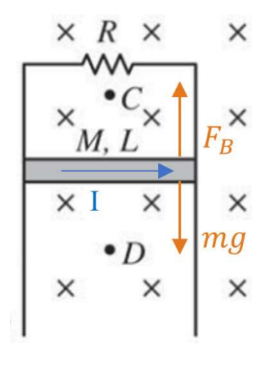
Example F: A conducting bar of mass M and length L is connected to two long vertical conducting rails. The two rails are connected by a resistor of resistance R at the top. The entire apparatus is in a magnetic field of magnitude B directed into this page. The bar is released from rest and slides without friction down the rails.
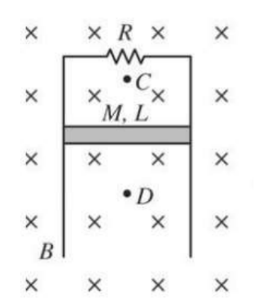
a) What is the direction of current in the resistor?
b) Is the magnitude of the net magnetic field above the bar at point C greater than, less than, or equal to the magnitude of the net magnetic field before the bar is released?
c) Determine an expression for the terminal velocity of the bar.
d) Derive an expression for the power dissipating in the resistor when the bar is at terminal velocity.
e) Derive an expression for the velocity of the bar as a function of time until it reaches terminal
velocity.
Answer/Explanation
a) Due to the downward motion due to gravity of the bar, the magnetic field into the page will push positive charge in the bar to the right due to the right-hand rule, causing a clockwise-current. The current in the resistor is to the left.
b) The induced current in the bar creates a magnetic field out of the page on top of the bar and into the page below the bar by the right hand-rule. Above the bar, this field goes against the existing field, so the net magnetic field in C decreases.
c) Due to the right hand rule again, the current to the right causes an upward magnetic force. With a downward force of gravity the forces on the bar are:
$
\begin{aligned}
& \sum_{\rightarrow m a} F=m g=m g-F_B \\
& \rightarrow m g-B I L
\end{aligned}
$
The current is based on the induced emf in the bar:
$
\begin{aligned}
& \rightarrow m a=m g-B\left(\frac{\varepsilon}{R}\right) L=m g-B\left(\frac{B L v}{R}\right) L \\
& \rightarrow m a=m g-\frac{B^2 L^2 v}{R}
\end{aligned}
$
At terminal velocity, the acceleration is zero:
$
\begin{aligned}
& 0=m g-\frac{B^2 L^2 v_T}{R} \rightarrow m g=\frac{B^2 L^2 v_T}{R} \\
& \rightarrow \boldsymbol{v}_{\boldsymbol{T}}=\frac{\boldsymbol{m} \boldsymbol{R g}}{\boldsymbol{B}^2 \boldsymbol{L}^2}
\end{aligned}
$
$
\begin{aligned}
& \text { d) Power }=I^2 R=\left(\frac{\varepsilon}{R}\right)^2 R=\frac{\left(B L_T\right)^2}{R^2} R \\
& \rightarrow P=\frac{B^2 L^2 v_T^2}{R}=\frac{B^2 L^2\left(\frac{m R g}{B^2 L^2}\right)^2}{R}=\frac{m^2 R^2 g^2}{B^2 L^2 R} \\
& \rightarrow P=\frac{m^2 R g^2}{B^2 L^2}
\end{aligned}
$
e) From c) $m a=m g-\frac{B^2 L^2 v}{R}$
$
\rightarrow m \frac{d v}{d t}=m g-\frac{B^2 L^2 v}{R}
$
This is a free-fall terminal velocity question like in AP Physics C: Mechanics, just with a different drag force.
To get v positive and without and cofficients (to make integration easy), multiply both sides by $-\frac{R}{B^2 L^2}$
$
\rightarrow-\frac{m R}{B^2 L^2} \frac{d v}{d t}=v-\frac{m R g}{B^2 L^2}
$
Separate the variables:
$
\frac{d v}{v-\frac{m R g}{B^2 L^2}}=-\frac{B^2 L^2}{m R} d t
$
This is a free-fall terminal velocity question like in AP Physics C: Mechanics, just with a different drag force.
To get $\mathrm{v}$ positive and without and cofficients (to make integration easy), multiply both sides by $-\frac{R}{B^2 L^2}$ $\rightarrow-\frac{m R}{B^2 L^2} \frac{d v}{d t}=v-\frac{m R g}{B^2 L^2}$
Separate the variables:
$
\frac{d v}{v-\frac{m R g}{B^2 L^2}}=-\frac{B^2 L^2}{m R} d t
$
The velocity starts at zero and goes to some value at time, $\mathrm{v}(\mathrm{t})$.
$
\begin{aligned}
& \int_0^{v(t)} \frac{d v}{v-\frac{m R g}{B^2 L^2}}=\int_0^t-\frac{B^2 L^2}{m R} d t \\
& \rightarrow \ln \left|v-\frac{m R g}{B^2 L^2}\right| v(t)=-\frac{B^2 L^2}{m R} t \rightarrow \ln \left|v(t)-\frac{m R g}{B^2 L^2}\right|-\ln \left|-\frac{m R g}{B^2 L^2}\right|=-\frac{B^2 L^2}{m R} t \rightarrow \ln \left|\frac{v(t)-\frac{m R g}{B^2 L^2}}{-\frac{m R g}{B^2 L^2}}\right|=-\frac{B^2 L^2}{m R} t \\
& \rightarrow \frac{v(t)-\frac{m R g}{B^2 L^2}}{-\frac{m R g}{B^2 L^2}}=e^{-\frac{B^2 L^2}{m R} t} \\
& \rightarrow \boldsymbol{v ( t )}=\frac{\boldsymbol{m R g}}{B^2 L^2}\left(\mathbf{1}-\boldsymbol{e}^{-\frac{B^2 L^2}{m R} t}\right)
\end{aligned}
$
By this equation, the velocity starts at 0 and increases asymptotically to $\frac{m R g}{B^2 L^2}$, which is the terminal velocity from c).