- If charge is evenly distributed on an object, it can thought of as being concentrated at its center, much like the force of gravity.
- The net charge on an object is determined by the difference between the number of electrons and the number of protons the object contains.
Calculate electrostatic force.
Coulomb’s Law
- Charges attract/repel each other by the electrostatic force.
- Electrostatic force is a vector quantity; the direction of the force depends on the sign (+/-) of the charges exerting force on each other. The direction of the force is along the line connecting the charges.
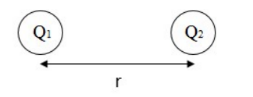
$\begin{array}{rr}|\vec{F}|=\frac{k\left|Q_1 Q_2\right|}{r^2} \\ k=8.99 \times 10^9 \frac{N^2}{C^2} & \frac{1}{4 \pi \epsilon_0}\end{array}$
- $\epsilon_0-$ permittivity of free space, measure of resistance to formation of electric field in a vacuum
$
\epsilon_0=8.85 \times 10^{-12} \frac{C^2}{N m^2}
$ - Superposition Principle: The net electrostatic force on a charge is the sum of all the forces from all the individual charges acting on it.
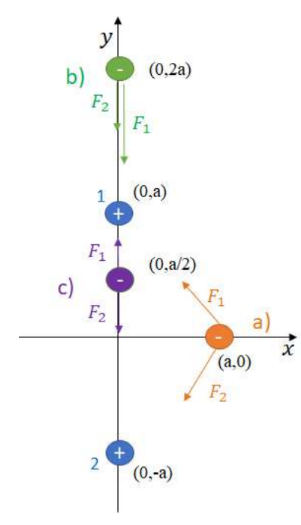
Example A: Example A: Positive point charges of equal magnitude Q are located at (0,a) and (0,−a).
(a) Find the total force the two charges exert on a charge -Q at (a,0).
(b) Find the total force the two charges exert on a charge -Q at (0,2a).
(c) Find the total force the two charges exert on a charge -Q at (0, a/2).
Answer/Explanation
<p(a) The y-component of the force cancels due to symmetry so only the $x-$ component needs to be calculated. Both forces point in the negative $\mathrm{x}$ direction and are equal in magnitude:$
\begin{aligned}
& F=-2 \frac{k|Q \|-Q|}{r^2} \cos \theta=-2 \frac{k Q^2}{\left(\sqrt{a^2+a^2}\right)^2} \frac{a}{\sqrt{a^2+a^2}} \\
& \rightarrow F=-\frac{2 k Q^2}{2 a^2} \frac{\sqrt{2}}{2} \rightarrow \boldsymbol{F}=-\frac{\boldsymbol{k} Q^2 \sqrt{2}}{2 a^2}
\end{aligned}
$
(b) Both forces act downwards in the y-direction. The negative charge is attracted to the positive charges, both of which are below it.
Answer/Explanation
<p$\begin{aligned} & F=-\frac{k|Q \|-Q|}{(2 a-a)^2}–\frac{k|Q \|-Q|}{(2 a-(-a))^2}=-\frac{k Q^2}{a^2}-\frac{k Q^2}{(3 a)^2}=-\frac{k Q^2}{a^2}-\frac{K Q^2}{9 a^2} \\ & \rightarrow \boldsymbol{F}=-\frac{\mathbf{1 0} k Q^2}{\mathbf{9 a}^2}\end{aligned}$(c) Both forces are in the $y$-direction. The force due to the charge at $(0, a)$ is positive and the charge due to $(0$,-a) is negative.
$
\begin{aligned}
& F=\frac{k|Q||-Q|}{\left(2 a-\frac{a}{2}\right)^2}-\frac{k|Q||-Q|}{\left(-2 a-\frac{a}{2}\right)^2}=\frac{k Q^2}{\left(\frac{3}{2} a\right)^2}-\frac{k Q^2}{\left(-\frac{5}{2} a\right)^2}=\frac{k Q^2}{\frac{9}{4} a^2}-\frac{k Q^2}{\frac{25}{4} a^2} \\
& \rightarrow \boldsymbol{F}=\frac{\mathbf{6 4 k Q ^ { 2 }}}{\mathbf{2 2 5} a^2}
\end{aligned}
$
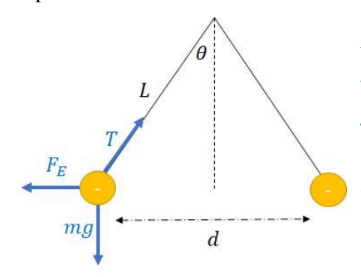
Example B: Two small pith balls of mass .5 kg each are suspended by strings of length L = .3 m from a
common point. They are both negatively charged and repel each other, remaining d = 0.1 m apart at
equilibrium. Find the excess number of electrons on each pith ball.Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Answer/Explanation
$\begin{aligned}
& \sum F_y=0=T \cos \theta-m g \rightarrow T=\frac{m g}{\cos \theta} \\
& \rightarrow T=\frac{(0.5 \mathrm{~kg})\left(10 \frac{m}{s^2}\right)}{\frac{\sqrt{(.3 m)^2-\left(\frac{1}{2} m\right)^2}}{.3 m}}=5.08 \mathrm{~N}
\end{aligned}
$
$
\begin{aligned}
& \sum F_x=0=T \sin \theta-F_E \rightarrow F_E=(5.08 N) \frac{\frac{1}{2} m}{.3 m}=0.85 N \\
& F_E=\frac{k Q^2}{r^2} \rightarrow Q=\sqrt{\frac{F_E r^2}{k}}=9.71 \times 10^{-7} \mathrm{C}
\end{aligned}
$
Charge is due to an integer number of excess electrons. To find this amount of electrons, divide the total charge by the fundamental charge, which the charge of a single electron $\left(1.6 \times 10^{-19} \mathrm{C}\right)$.
Example C: A charge Q is uniformly distributed from x = −a to x = 0. Find the force that charge distribution exerts on a charge Q located at x = a.
Answer/Explanation
<p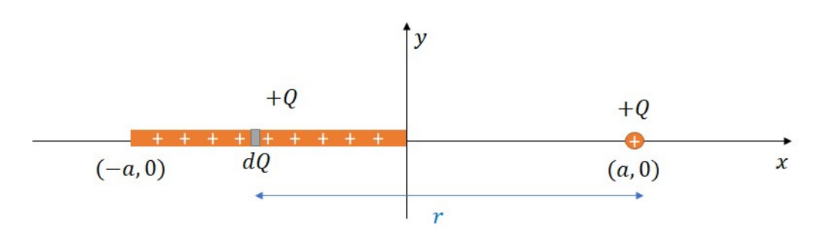
*dQ is an infinitesimally small charge, the charge is equal to $\lambda d x$, where $\lambda$ is the linear charge density of the line of charge. The charge density is the total charge over the length so $\lambda=\frac{Q}{a}$.
${ }^* \mathrm{r}$, the distance between the point charge and dQ, is a variable that changes as a function of $\mathrm{x}$, in this case, $r=$ $a-x$, as $\mathrm{x}$ is always negative.
$\begin{aligned} & d F=\frac{k Q \lambda d x}{r^2} \rightarrow d F=\frac{k Q \frac{Q}{a} d x}{(a-x)^2} \\ & \rightarrow F=\frac{K Q^2}{a} \int_{-a}^0 \frac{d x}{(a-x)^2} \rightarrow F=\frac{K Q^2}{a}\left(\frac{1}{a-x}\right){ }_{-a}^0 \rightarrow F=\frac{k Q^2}{a}\left(\frac{1}{a}-\frac{1}{2 a}\right) \\ & \rightarrow \boldsymbol{F}=\frac{\boldsymbol{k} Q^2}{\mathbf{2 a}}\end{aligned}$