Focus Question: What is Gauss’s Law?
- To use Gauss’s Law, a surface called a Gaussian surface must be selected (pretty much always a cylinder or sphere). It is not necessarily a surface of the object being analyzed.
- The symmetry of the closed surface makes it possible to evaluate $\oint E \cdot d A$, often without scary calculus.
- If $E$ is perpendicular to the Gaussian surface, and of constant magnitude, then $\oint E \cdot d A=E A$.
- If $\mathrm{E}$ is parallel to the Gaussian surface, then $\oint E \cdot d A=0$.
- The following problems look at various charge distributions. Charge can be distributed along any conducting surface (this is not a Gaussian surface, which is something we make up to solve problems).
Example A: Infinite Sheet – An infinite plane has uniform charge density of $\sigma$. Find the electric field due to the plane.
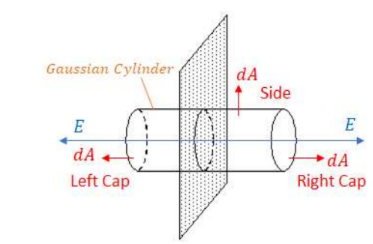
A large plane of charge has field going outwards on both sides, so the chosen Gaussian surface needs to have symmetry going out from two ends. A cylinder will be used here since there the dA symmetry of the caps matches the field. The flux is then:
$
\phi=\phi_{\text {LEFT CAP }}+\phi_{\text {RIGHT CAP }}+\phi_{\text {STDE }}
$
For the side, dA is perpendicular to $\mathrm{E}$, so there is no flux. For the two caps, $\mathrm{E}$ and $\mathrm{dA}$ are in the same direction so $\int E \cdot d A \cos \theta=E A$ for both.
$
\phi=\int E \cdot d A_{L E F T}+\int E \cdot d A_{R I G H}=\frac{Q_{e n c}}{\varepsilon_0}
$
The charge enclosed for both is the charge density, $\sigma$, multiple by the cap area, A.
$
\phi=E A+E A=\frac{\sigma A}{\varepsilon_0} \rightarrow \boldsymbol{E}=\frac{\boldsymbol{\sigma}}{2 \varepsilon_0}
$
*The field lines of the sheet are straight, parallel, uniformly spaced and perpendicular to the sheet. The calculation assumes an infinitely large sheet, but the results are a reasonable approximation for a large sheet. When a conducting plate is given a charge, the charge distributes itself uniformly over the entire surface of the plate. The electric field is directed away from the plate.
Example B: Parallel plates of equal charge – Find the electric field a) outside the plates and b) inside the plates.
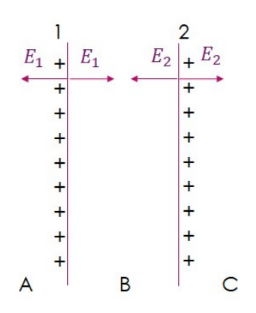
Both plates are conductors, so charge gathers on the surface, in this case the charge gathers on the outside surface as they repel. Both plates have fields of $\frac{\sigma}{2 \varepsilon_0}$ as found in Example A.
a) Outside the plates, in either regions $\mathrm{A}$ or $\mathrm{C}$, the fields point in the same direction: $E=E_1+E_2=\frac{\sigma}{2 \varepsilon_0}+\frac{\sigma}{2 \varepsilon_0}=\frac{\sigma}{\varepsilon_0}$
b) In the region inside the plates, $E_1$ and $E_2$ are in opposite directions:
$
E=E_1+E_2=\frac{\sigma}{2 \varepsilon_0}-\frac{\sigma}{2 \varepsilon_0}=\mathbf{0}
$

- When parallel plates are given equal and opposite charges, the field is nearly uniform in the space between the plates. Most of the charge is in the inner surface of the plates, which very little charge on the outside of the plates.
- The electric field is the resultant of the fields due to the two sheets of charge.
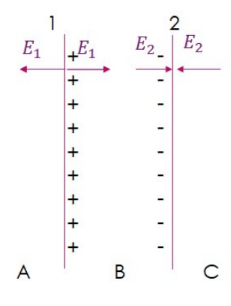
In the region between the plates, both fields point from the positive plate to the negative plates, so the contributions from each plate adds:
$
E=E_1+E_2=\frac{\sigma}{2 \varepsilon_0}+\frac{\sigma}{2 \varepsilon_0}=\frac{\sigma}{\varepsilon_0}
$
- Using Gauss’s Law
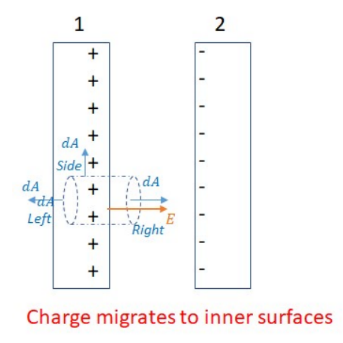
A Gaussian cylinder is drawn that goes through the surface of one of the plates: $\phi=\phi_{\text {AIF }}+\phi_{\text {RIGHT CAP }}+\phi_{\text {StDE }}$
The side has no flux since $\mathrm{E}$ is perpendicular to $\mathrm{dA}$ of the lateral side of the cylinder. The left cap has no field through it. For the right cap, E and dA are in the same direction so $\int E \cdot d A \cos \theta=E A$.
The charge enclosed by the Gaussian cylinder is the charge density of the plate times the area of the cap of the cylinder passing through the plate:
$
\emptyset=\oint \vec{E} \cdot \overrightarrow{d A}=\frac{Q_{\text {enc }}}{\epsilon_0} \rightarrow E A=\frac{\sigma A}{\varepsilon_0} \quad \rightarrow \boldsymbol{E}=\frac{\sigma}{\varepsilon_0}
$
Example C: Infinite Line Charge – Determine the electric field a distance R from an infinitely long conducting wire with a uniform charge density of λ.
Answer/Explanation
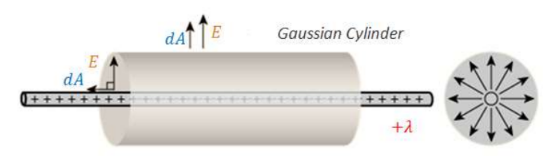
The line of charge has field going radially outward along the line. The lateral ends of a cylinder have symmetry to match this, so a Gaussian cylinder will be used. Field does not go through the caps of the cylinder, so only the lateral edge will be used:
$\emptyset=\oint \vec{E} \cdot \overrightarrow{d A}=\frac{Q_{e n c}}{\varepsilon_0}$
$\int d A$ is the lateral surface area since that is the surface with flux through it. The charge of the line inside the cylinder is the linear charge density, $\lambda$, multiplied by the length of the cylinder, L.
$
\phi=E \int d A=\frac{\lambda L}{\varepsilon_0} \rightarrow E(2 \pi r E)=\frac{\lambda t}{\varepsilon_0} \quad \rightarrow E=\frac{\lambda}{2 \pi r \varepsilon_0}
$
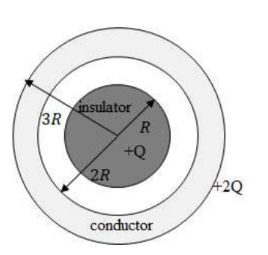
Example D: A sphere of radius R is surrounded by a concentric spherical shell of inner radius 2R and outer radius 3R, as shown The inner sphere is an insulator containing a net charge +Q distributed uniformly throughout its volume. The spherical shell is a conductor containing a net charge +2Q. Use Gauss’s law to determine the electric field for the following values of r, the distance from the center of the insulator.
a) $0<r<R$
b) R $<$ r $<2 R$
c) $2 \mathrm{R}<\mathrm{r}<3 \mathrm{R}$
d) $r>3 R$
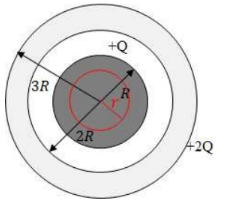
Spheres obviously have spherically symmetry, so Gaussian spheres will be used for all regions.
a) A charge insulator has its charge uniformly distributed throughout. The charge enclosed by the Gaussian surface is the charge density of the entire region multiplied by the volume enclosed by the Gaussian surface.
$\emptyset=\oint \vec{E} \cdot \overrightarrow{d A}=\frac{Q_{e n c}}{\varepsilon_{\mathbf{0}}} \rightarrow E \int d A=\frac{\rho V_{G A U S S I A N}}{\varepsilon_{\mathbf{0}}}$
$\int d A$ is the surface area of the Gaussian surface.
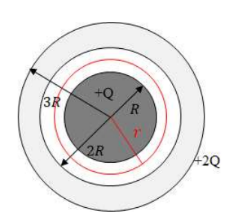
b) The charge enclosed is total charge of the insular, $+Q$.
$
\begin{aligned}
\emptyset=\oint \vec{E} \cdot \overrightarrow{d A} & =\frac{Q_{e n c}}{\varepsilon_0} \rightarrow E\left(4 \pi r^2\right)=\frac{Q}{\varepsilon_0} \\
& \rightarrow E=\frac{Q}{4 \pi r^2 \varepsilon_0}
\end{aligned}
$
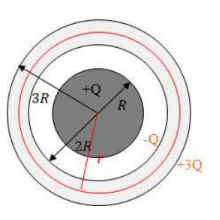
c) The outer shell is a conductor, so all charge gathers on the outer and inner surfaces. A charge of -Q gathers on the inner surface as it’s attracted to the insular. The excess charge, +3Q, gathers on the outer shell. The charge enclosed by the Gaussian surface is zero.
$\emptyset=\oint \vec{E} \cdot \overrightarrow{d A}=\frac{Q_{e n c}}{\varepsilon_0} \rightarrow Q_{e n c}=0 \quad \rightarrow \boldsymbol{E}=\mathbf{0}$
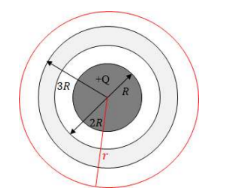
d) The total charge enclosed in this case if $+3 Q$.
$
\emptyset=\oint \vec{E} \cdot \overrightarrow{d A}=\frac{Q_{e n c}}{\varepsilon_0} \rightarrow E\left(4 \pi r^2\right)=\frac{3 Q}{\varepsilon_0} \quad \rightarrow E=\frac{3 Q}{4 \pi r^2 \varepsilon_0}
$
Example F: A very long, solid, non-conducting cylinder of radius R has a positive charge of uniform volume density ρ. A section of the cylinder far from its ends is shown below. Let r represent the radial distance from the axis of the cylinder.

a) Derive an expression for the magnitude of the electric field at a radius r < R.
b) Derive an expression for the magnitude of the electric field at a radius r > R.
A Gaussian cylinder will be used for both cases as the radially linear symmetry of a cylinder obviously matches the field produced by a cylinder.
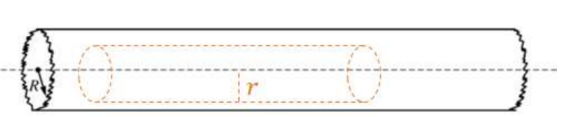
a) The cylinder is a conductor, so all charge is on the outer surface, so there is no charge enclosed by the Gaussian cylinder:
$
\emptyset=\oint \vec{E} \cdot \overrightarrow{d A}=\frac{Q_{e n c}}{\varepsilon_0} \rightarrow Q_{e n c}=0 \quad \rightarrow \boldsymbol{E}=\mathbf{0}
$
b) $\emptyset=\oint \vec{E} \cdot \overrightarrow{d A}=\frac{Q_{\text {enc }}}{\varepsilon_0}$
$
\phi=E \int d A=\frac{\rho V_{e n c}}{\varepsilon_0}
$
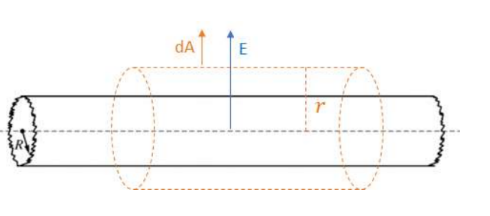
Since the charge is only contained in the actual cylinder of radius $\mathrm{R}$, the volume of the cylinder of radius $\mathrm{R}$ will be used when finding the charge enclosed:
$
\begin{aligned}
& \rightarrow E(2 \pi r L)=\frac{\rho \tilde{H} R^2 t}{\varepsilon_0} \\
& \rightarrow E=\frac{\rho R^2}{2 r \varepsilon_0}
\end{aligned}
$
Rate your understanding: Gauss’s Law
