Focus Question: What causes a magnetic field?
Answer/Explanation
- Laws of Magnetism – Magnets have 2 poles. Like poles repel, opposite poles attract.
Cause of Magnetism – A charge in motion creates a magnetic field in the space around it.
*Electric fields describe interaction between charges at rest. Magnetic fields describe interactions between charges in motion.
Ferro-magnet – naturally occurring magnet caused by clusters of atoms with electrons spinning in the same direction.
Magnetic Field – a region of space surrounding a magnet in which magnetic forces are applied to other magnets.
- All magnets are dipoles, they have a north and a south.
- Like poles repel; opposites attract – Magnetic field lines form closed loops.
By convention, field lines exit north and enter south.
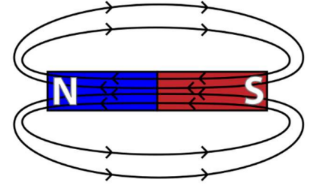
*The earth is a magnet. There is a south pole at the north pole, so the north pole of a bar magnet is attracted to the earth’s geographic north.
Solve problems involving a charge particle moving in an electric field.
- A moving charge sets up a magnetic field around it.
- The magnetic field exerts a force on a moving charge in a field.
- Field direction: Direction of the magnetic force is perpendicular to both the magnetic field and the direction of the moving charge; the magnetic force does no work on a moving charge.
- The right hand rule is used for positive particles (left hand for negative)
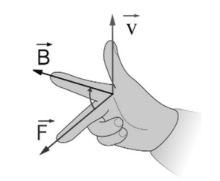
- Force:

$
\vec{F}=q \vec{v} \times \vec{B}=B q v \sin \theta
$
$B$ – magnetic field
$
B=\frac{\mu_0 I}{2 \pi r}
$
Example A: A uniform magnetic field $B=0.20 \mathrm{~T}$ points in the positive y-direction. If $q=3.5 \times 10^{-6} \mathrm{C}$ and the speed of the charge is $8.0 \times 10^7 \mathrm{~m} / \mathrm{s}$ (making a $45^{\circ}$ degree angle in the $-\mathrm{x},+\mathrm{z}$ as shown) then what is the magnitude and direction of the force on the charge?
Answer/Explanation
$\begin{gathered}F=q \vec{v} \times \vec{B} \\ \vec{v}=\left(-\left(8 \times 10^7 \frac{m}{s}\right) \cos 45^{\circ}\right) \hat{\imath}+\left(\left(8 \times 10^7 \frac{m}{s}\right) \sin 45^{\circ}\right) \hat{k} \\ B=(.2 T) \hat{\jmath}\end{gathered}$
$\begin{aligned} & F=q \vec{v} x \vec{B}=\left(3.5 \times 10^{-6} C\right)\left|\begin{array}{ccc}\hat{\imath} & \hat{\jmath} & \hat{k} \\ -8 \times 10^7 \frac{\sqrt{2}}{2} & 0 & 8 \times 10^7 \frac{\sqrt{2}}{2} \\ 0 & 0.2 & 0\end{array}\right| \\ & F=(-40 \hat{\imath}-40 \hat{k}) N \\ & \end{aligned}$
Example B: Determine the direction of the unknown variable for an electron using the coordinate axis given.

Answer/Explanation
Since an electron is negatively solved, each of these can be found using the left-hand rule:
a) The magnetic force is out of the page (+z direction).
b) The magnetic field is into the page (-z direction).
c) The velocity is the right (+x direction).
Magnetic Force and circular motion
- Since force is always perpendicular to velocity, the magnetic force does no work and the speed of the charged particle is constant. The direction of velocity changes, but not the magnitude.
The magnetic force keeps the charged particle in the circle, supplying the centripetal force
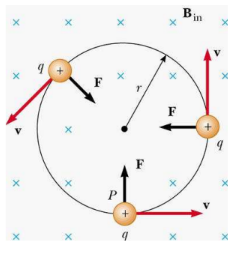
$\begin{aligned} & F_{\text {MAGNETIC }}=F_{\text {CENTRIPETAL }} \\ & B q v=\frac{m v^2}{r} \\ & \rightarrow B q=\frac{m v}{r} \\ & \end{aligned}$
Example C: A proton moves in a circular orbit of radius $0.5 \mathrm{~m}$ perpendicular to a uniform magnetic field of magnetic $0.3 \mathrm{~T}$. Find the period of the proton’s orbit. *the mass of a proton $=1.67 \times 10^{-2} \mathrm{~kg}$
Answer/Explanation
$
\begin{aligned}
& F_B=F_c \rightarrow B q v=\frac{m v^2}{r} \rightarrow v=\frac{B q r}{m} \\
& T=\frac{2 \pi r}{v}=\frac{2 \pi r}{\frac{B q r}{m}}=\frac{2 \pi m}{B q} \rightarrow T=\frac{2 \pi\left(1.67 \times 10^{-27} \mathrm{~kg}\right.}{(0.3 T)\left(1.6 \times 10^{-19} \mathrm{C}\right)}=2.2 \times 1 \mathbf{1 0}^{-7} \mathrm{~s}
\end{aligned}
$
The Lorentz Force
- A charge moving in the presence of both a magnetic and electric field experiences both an electric and magnetic force: Lorentz Force – total electric and magnetic forces on a moving charge:
$
\begin{gathered}
\vec{F}=\vec{F}_E+\vec{F}_B \\
\vec{F}=q \vec{E}+q \vec{v} x \vec{B}
\end{gathered}
$
Example D: A charge q moves with velocity v in a uniform magnetic field B.
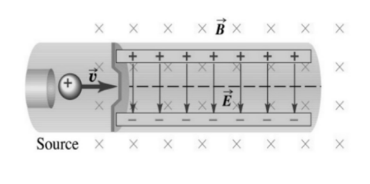
a) Specify the directions of the magnetic and electric forces.
b) What is the magnitude of E, the electric field, that must exist so that the charge passes un-defelected between the plates?
Answer/Explanation
a) The electric force is down since the electric field is down. A positive charge experiences a force in the direction of the electron field. By the right hand rule, the magnetic force is up.
b) $\sum F_y=0=F_B-F_E \rightarrow B q v=E q \rightarrow E=B \boldsymbol{V}$
Example E: Behold the system below. A positive charge $q$ with mass $m$ is accelerated from rest across a potential difference $V$ in region 2. It passes undeflected in region 2 due to an electric field. In region 3, no electric field acts. A magnetic field of $B$ acts in regions 2 and 3 .
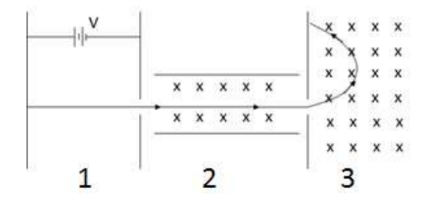
a) With what speed does the particle enter region 2?
b) What is the magnitude and direction of the electric field in region 2?
c) What is the radius of the circular path in region 3?
- In region 1, a potential difference does work on the charge to accelerate it from rest.
- In region 2, the particle travels undeflected due to an electric field simultaneously with the magnetic field.
- In region 3, the particle travels in a circular motion due to the uniform magnetic field in a semicircle until it hits a detector. The radius of the circular path causes the circular radii to be different for different elements.
Answer/Explanation
(a) $W=\Delta K$
$
\begin{aligned}
& W=\Delta K \\
& \Rightarrow V_q=\frac{1}{2} m V_f^2-\frac{1}{2} m V_i^2
\end{aligned}
$
(b) $F_B=F_E$
qv$B=E x \Rightarrow E=B v \Rightarrow E=B \sqrt{\frac{2 v q}{m}}$
Magnetic field is up by RHR, so electric field is down.
(c) $\begin{aligned} & F_B=F_c \\ & q \times B=\frac{m v^x}{r} \Rightarrow r=\frac{m v}{q B}=\frac{m \sqrt{\frac{V q}{m}}}{9 B} \\ \Rightarrow r & =\frac{\sqrt{V q m}}{9 B}\end{aligned}$