- Most capacitors have a solid, nonconducting material between the plates. This material is called a dielectric.
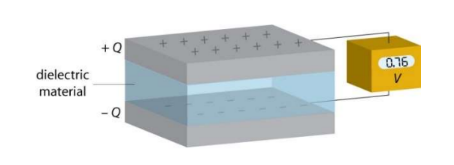
- Function of a dielectric:
- Keeps plates close, but not in contact
- Can tolerate greater field without dielectric breakdown
*Air is more suspect to dielectric breakdown, in which the insulator ionizes and charge can flow between the plates.
- Increases capacitance.
- The potential difference between two charge plates decreases when a dielectric is used, but the charge on each plate stays the same. Electric field decreases when a dielectric is inserted, due to small induced charges appearing on the surfaces of the dielectric.
- The dielectric constant, κ:
$\kappa=\frac{C}{C_0}$
$\mathrm{C}$ – Capacitance with dielectric
$\mathrm{C}_0$ – Capacitance without dielectric
$* \geq 1$
Field Decreases: $\kappa=\frac{V_0}{V}=\frac{E_0 d}{E d}=\frac{E_0}{E}$
Permittivity increases: $\varepsilon=\kappa \varepsilon_0$
Voltage:
Case 1: If the battery is no longer connected, voltage decreases $\kappa=\frac{Q / V}{Q / V_0}=\frac{V_0}{V}$ *in this case, energy decreases due to the work done to insert dielectric.
Case 2: If the capacitor is still connected to the battery, voltage remains constant *In this case, energy increases since capacitor increases and voltage is constant.
Example A: A $275 \mu \mathrm{F}$ capacitor will be manufactured using a dielectric having a permittivity of $4.00 \varepsilon_0$ and circular plates having a diameter of $2.50 \mathrm{~cm}$. What should the plate separation (and the thickness of the dielectric) be? Is it likely that this large a capacity could be constructed using parallel plate architecture?
Answer/Explanation
$
\begin{aligned}
& C=\frac{\kappa \varepsilon_0 A}{d} \rightarrow d=\frac{\kappa \varepsilon_0 A}{C} \\
& d=\frac{4\left(8.85 \times 10^{-12} \frac{C^2}{N m^2}\right)\left(\pi\left(\frac{.025}{2} \mathrm{~m}\right)^2\right)}{275 \times 10^{-6} \mathrm{~F}}=6.3 \times 10^{-11} \mathrm{~m}
\end{aligned}
$
It would be extremely difficult to construct a plate separation this small.
- Electric field in a dielectric using Gauss’ Law:
*induced charges appear on the surface of the dielectric.
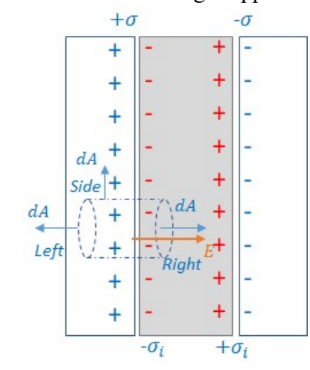
$\sigma$ : charge on plates $\quad \sigma_i:$ induced charge on dielectric surface
$
\begin{aligned}
& \emptyset=\oint \vec{E} \cdot \overrightarrow{d A}=\frac{Q_{e n c}}{\epsilon_0} \rightarrow E A=\frac{\left(\sigma-\sigma_i\right) A}{\varepsilon_0} \\
& \rightarrow E=\frac{\sigma-\sigma_i}{\varepsilon_0}
\end{aligned}
$
*Since the permittivity increases by a factor of $\kappa, \mathrm{E}$ is also $E=\frac{\sigma}{\kappa \varepsilon_0}$
Relationship between induced dielectric charge and dielectric constant:
$
\begin{aligned}
& \frac{\sigma-\sigma_i}{\varepsilon_\theta}=\frac{\sigma}{\kappa \varepsilon_\theta} \\
& \rightarrow \boldsymbol{\kappa}=\frac{\boldsymbol{\sigma}}{\boldsymbol{\sigma}-\boldsymbol{\sigma}_{\boldsymbol{i}}}
\end{aligned}
$
$\kappa=\frac{E_0}{E}$
- Energy density in dielectric
$
\text { Density }=\frac{U}{\text { Volume }}=\frac{\frac{1}{2} \kappa C V^2}{A d}=\frac{\frac{1}{2} \kappa \varepsilon_0 \frac{A}{d} E^2 d^2}{A d}=\frac{1}{2} \kappa \varepsilon_0 E^2
$
Example B: A parallel plate capacitor of area A and plate separation L is filled with a removable dielectric slab
of dielectric slab constant κ. The capacitor is given a charge Q with the slab removed, is disconnected from the
battery and then the slab is inserted.
a) Find the potential difference with and without the dielectric slab.
b) Find the electric field between the plates with and without the slab.
Answer/Explanation
c) Find the induced charge on the slab.
a) W/0 slab: $\quad V_0=\frac{Q}{C}=\frac{Q}{\varepsilon_0 \frac{A}{d}}=\frac{Q d}{\varepsilon_0 A}$ with slab: $K=\frac{V_0}{V} \Rightarrow V=\frac{V_0}{K}=\frac{Q d}{K \varepsilon_0 A}$
b) W/0 slab: $E_0=\frac{\sigma}{\varepsilon_0}=\frac{Q}{A \varepsilon_0}$ With slab: $K=\frac{E_0}{E} \Rightarrow E=\frac{Q}{K A \varepsilon_0}$
c)
$$
\begin{aligned}
& K=\frac{\sigma}{\sigma-\sigma_i} \Rightarrow \sigma-\sigma_i=\frac{\sigma}{K} \Rightarrow \sigma_i=\sigma-\frac{\sigma}{K} \\
\Rightarrow & \sigma_i=\frac{Q}{A}-\frac{Q}{A K} \Rightarrow \sigma=\frac{Q K-Q}{A K}
\end{aligned}
$$
Example C: A capacitor having no dielectric has a capacitance of C. It is charged up to V by momentarily attaching it to a battery, and then disconnecting it.
a) What is the energy stored in the capacitor at this voltage?
b) What is the charge on the capacitor?
c) A dielectric having a permittivity of 20 is now carefully inserted between the plates of the capacitor. What is its new capacitance?
d) What is the charge on the new capacitor?
e) What is the energy stored in the new capacitor?
f) Explain the discrepancy between (e) and (a).
Answer/Explanation
a) $U=\frac{1}{2} C V^2$
b) $Q=C V$
c) $\kappa=\frac{C^{\prime}}{C} \rightarrow C^{\prime}=\kappa C$
d) $Q=C^{\prime} V=\kappa C V$
*Inserting a dielectric increases the charge by a factor of kappa: $\kappa=\frac{Q}{Q_0}$
e) $U=\frac{1}{2} \frac{Q^2}{C}$ The charge and the capacitance both increase by a factor of the dielectric constant:
$
U=\frac{1}{2} \frac{(\kappa C V)^2}{\kappa C}=\frac{1}{2} \kappa C V^2
$
f) The energy increased by a factor of the dielectric constant even though the circuit was not connected to power. The work done to insert the dielectric was converted to energy stored in the capacitor.
Rate your understanding: Dielectrics
