How are displacement, acceleration, and velocity related?
➢ Motion occurs whenever an object changes position. Unlike dynamics, which is the study of motion and forces, kinematics only considers the motion of objects without any regard to force. Kinematics is focused with looking at how vector and scalar quantities change while a particle is in motion. Understanding the difference between scalar (distance, speed, etc.) and vector (displacement, velocity, acceleration, etc.) quantities is key to kinematics.
➢ Scalars are quantities that only have a magnitude assigned to them, while vectors have direction and magnitude. Displacement is a scalar quantity and is given by ∆𝑥 = 𝑓𝑖𝑛𝑎𝑙 𝑝𝑜𝑠𝑖𝑡𝑖𝑜𝑛 − 𝑖𝑛𝑖𝑡𝑖𝑎𝑙 𝑝𝑜𝑠𝑖𝑡𝑖𝑜𝑛, while distance is simply the length of the path traveled.
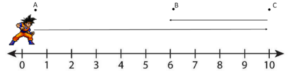
*For example, suppose Goku goes from point A to point C, then to point B. His distance is 14, since he travels 10 in the positive direction to get to B, and 4 in the negative direction to get to point B. However, displacement is 6.
Calculate average and instantaneous velocity.
Speed is the rate at which an object covers distance, while velocity is the rate of change of displacement. An object’s average velocity can be found over a time interval using the endpoints. In Physics C, the instantaneous velocity can also be found by taking the instantaneous rate of change of position.
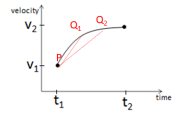
Average Velocity Instantaneous Velocity
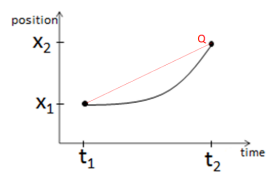
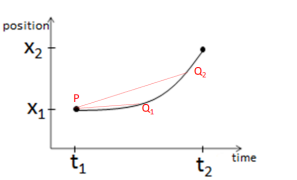
The average speed is the slope of the line As Q gets closer to P, the average velocity is found for
connecting the segments. shorter and shorter times. Instantaneous velocity
velocity is defined as the limiting average velocity as
Q approaches P.
\( v = \lim_{\Delta tx \mapsto x^2 0}\frac{\Delta x}{\Delta t}=\frac{dx}{dt}\)
* In Physics C, “Speed” can mean two different things:
▪ Average speed is found simply by 𝑠𝑝𝑒𝑒𝑑 \(=\frac{distance}{time},\) or by taking the magnitude of the average velocity vector.
▪ Instantaneous speed is the magnitude of the instantaneous velocity vector.
Important rules for positive vs. time graphs
▪ The slope of the graph represents velocity.
*slope is change in y over change in x, ∆𝑦/∆𝑥, not y/x.
▪ A line means constant velocity.
▪ A horizontal line means the object is at rest.
▪ A parabola means constant acceleration.
\(a=\frac{dv}{dt}=\frac{d}{dt}\left ( \frac{dx}{dt} \right )=\frac{d^{2}x}{dt^{2}}\) concavity

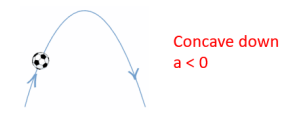
▪ When the graph crosses the x-axis the object is at the origin.
*A position vs. time graph does not show the shape of an object’s trajectory.
Example A: Ponder the position vs. time graph shown below. At which point(s) is velocity?
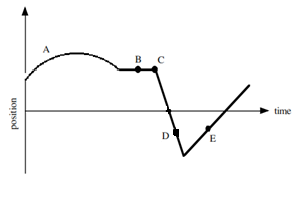
a) constant?
Answer/Explanation
Ans: This occurs anywhere where there is a straight line. B, D, E
b) zero?
Answer/Explanation
Ans: This is where position is not changing (a horizontal line) B
c) negative?
Answer/Explanation
Ans: This occurs when slope is negative D
d) undefined?
Answer/Explanation
Ans: Slope is undefined at sharp curves, which occurs at C
e) At which points are speed decreasing?
Answer/Explanation
Ans: Speed is decreasing when the magnitude of the slope is decrease, which occurs at A
Calculate average and instantaneous velocity.
▪ Acceleration – Rate of change of velocity.
Average Acceleration Instantaneous Acceleration

Average acceleration \(=\frac{\Delta velocity}{\Delta tim}\) \(a=\lim_{\Delta t\rightarrow 0}\frac{\Delta v}{\Delta t}=\frac{dv}{dt}\)
\(a=\frac{\Delta v}{\Delta t}=\frac{d}{dt}\left ( \frac{dx}{dt} \right )=\frac{d^{2}x}{dt^{2}}\)
Important rules for velocity vs. time graphs
▪ The slope of the graph represents acceleration. The area under the graph represents displacement.
▪ A line means constant acceleration. A horizontal line means constant velocity.
▪ When the graph crosses the x-axis the object switches direction.
Relationship between Velocity and Acceleration
If velocity and acceleration have the same sign, an object is motion is speeding up.
▪ 𝑎 > 0, 𝑣 > 0 : speeding up in positive direction
▪ 𝑎 < 0, 𝑣 < 0 : speeding up in negative direction
▪ 𝑎 > 0, 𝑣 < 0 : moving in negative direction and slowing down
▪ 𝑎 < 0, 𝑣 > 0 : moving in positive direction and slowing down
*On a velocity vs time graph, speed is increasing when a graph is moving away from the x-axis and is decreasing when the graph approaches the x-axis.
Solve for kinematic quantities when acceleration is constant.
When acceleration is constant, the 5 kinematic equations from Physics 1 can be used. When given a problem to solve for an unknown quantity, find a kinematics equation that contains both the unknown and the known quantities. Each equation contains four quantities and can be classified by the quantity not in the equation.
1. No acceleration: The no acceleration kinematic equation simply states that displacement of an object during a certain frame of time is the average velocity multiplied by the amount of time:
\(\Delta x=\left ( \frac{v_{i}+v_{f}}{2} \right )\Delta t\)
2. No displacement: The no displacement formula comes from the definition of acceleration:
\(a = \frac{\Delta v}{\Delta t}=\frac{v_{f}-v_{i}}{\Delta t}\rightarrow v_{f}=v_{i}+a\Delta t\)
3. No final velocity: Equation 2 can be written as to find the velocity as some time, 𝑣(𝑡), as 𝑣(𝑡) = 𝑣𝑖 + 𝑎𝑡.
Since velocity is the rate of change of position, the displacement can be found by integrating the velocity function.
\(\Delta x=\int vdt\rightarrow \Delta x=\int (v_{i}+at)dt\rightarrow \Delta x=v_{i}\Delta t+\frac{1}{2}a\Delta t^{2}\)
4. No initial velocity: Rearranging equation 2 and then integrating gives: \(\Delta x=v_{f}\Delta t-\frac{1}{2}a\Delta t^{2}\)
5. No time: The no time equation can be derived by combing (1) and (2):
Solving (2) for t: \(\Delta t=\frac{v_{f}-v_{i}}{a}\)
Plugging this result into \((1):\Delta x=\left ( \frac{v_{i}+v_{f}}{2} \right )\left ( \frac{v_{f}+v_{i}}{a} \right )\rightarrow \Delta x=\frac{v_{f}^{2}-v_{i}^{2}}{2a}\rightarrow v_{f}^{2}=v_{i}^{2}+2a\Delta x\)
Example B: A Hyundai Elantra is travelling to Homeplus at 32 m/s when it brakes with constant deceleration. It takes the car 9 seconds to stop.
a) What is the acceleration?
Answer/Explanation
Ans:
Since the acceleration is constant, the kinematics equations can be used.
Known variable: \(v_{i}=32\frac{m}{s},\Delta t=9 s, v_{f}=0\frac{m}{s}(car stops)\)
Unknown variable: 𝑎
Equation that relates the variables: \(v_{f}=v_{i}+a\Delta t\)
Solving the equation for acceleration: \(a=\frac{v_{f}-v_{i}}{\Delta t}\)
\(a=\frac{0\frac{m}{s}-32\frac{m}{s}}{9s}=-3.6\frac{m}{s^{2}};\) the acceleration is negative since the object has positive velocity and is slowing down.
b) What is the car’s stopping distance?
Answer/Explanation
Ans:
Since 4 kinematics quantities are known, any of the equations that include displacement can be used.
Since the object in car in this problem is always moving in the positive direction, the distance is equal to the displacement.
\(\Delta x=\left ( \frac{v_{i}+v_{f}}{2} \right )\Delta t=\left ( \frac{32\frac{m}{s}-\frac{0m}{s}}{2} \right )(9s)=144m\)
Example C: In order to satiate his extreme need for speed, Faisal drives down Southern Boulevard at 36 m/s.
At one instant, he passes the car of a concerned police officer. The police car starts from rest to pursue with a constant acceleration of 3.0 m/s2.
a) How long will it take the police officer to catch the delinquent speeder?
Answer/Explanation
Ans:
Both Faisal (F) and the Police Officer (P) start at the same position. The police officer will catch up to Faisal when they have equal positions.
Faisal’s position function – Faisal has constant velocity, so his position is simply his velocity times time: 𝑥𝐹(𝑡) = 32𝑡
Police Officer’s position function: The police officer starts at rest and has constant acceleration, so one of the kinematic equations is to be used: ![]()
Equating the position functions and solving for the time when they are equal: ![]()
b) How far will the police car have traveled?
Answer/Explanation
Ans: ![]()
c) How fast is the police officer traveling when he catches up?
Answer/Explanation
Ans: Since the police officer starts from rest with constant acceleration of 3, his velocity as a function of time is given as 𝑣𝑃(𝑡) = 𝑣𝑖 + 𝑎𝑡 → 𝑣𝑃(𝑡) = 3𝑡
𝑣𝑃(𝑡) = 3(21.3 𝑠) = 𝟔𝟒 𝒎/s
Solve for kinematic quantities when acceleration is not necessarily constant.
▪ If acceleration varies as a function of time, the kinematics equations are not valid. However, calculus is:
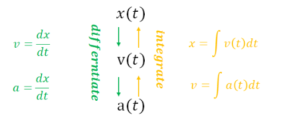
Velocity is the derivative of position: \(v = \frac{dx}{dt}\)
Acceleration is the first derivative of velocity and the second derivative of position: \(\alpha = \frac{dv}{dt}=\frac{d^{2}x}{dt^{2}}\)
▪ Reversing the process used to find 𝑣(𝑡) or 𝑎(𝑡), you can integrate 𝑣(𝑡) to find 𝑥(𝑡) or 𝑎(𝑡) to find 𝑣(𝑡)
▪ To find maxima and minima, look at end points and critical points (points where the slope is zero).
Example D: A at x = 5 m is traveling at 2 m/s at time t = 0 s. It moves with an acceleration given by \(a(t)=\left ( 2\frac{m}{s^{3}} \right )t-3\frac{m}{s}.\)
a) Find a function for v(t)
Answer/Explanation
Ans: \(v(t)=\int a(t)dt=t^{2}-3t+c\)
Since v(0) = 2 m/s, C = 2, making the velocity function: 𝒗(𝒕) = 𝒕𝟐 − 𝟑𝒕 + 𝟐
b) Find the minimum velocity of the particle.
Answer/Explanation
Ans: To find the minimum velocity, the points where the slope changes signs (where the derivative of velocity is zero) must be found. In addition, this must be compared to the endpoints. There is no endpoint on the right, but t = 0 is an endpoint.
\(v'(t)=2t-3=0. v'(t)=0 at t = \frac{3}{2}, \) so a relative extrema occurs at this point.
\(v\left ( \frac{3}{2} \right )=\left ( \frac{3}{2} \right )^{2}-3\left ( \frac{3}{2} \right )+2=-.25\frac{m}{s}\)
Since the function is a parabola that opens up and the endpoint is v(0) 2 m/s, –.25 m/s is the minimum value of the velocity.
c) Find a function for x(t).
Answer/Explanation
Ans: \(x(t)=\int v(t)dt=\frac{1}{3}t^{3}-\frac{3}{2}t^{2}+2t+c\)
Since x(0) = 5 m, C = 5, making the position function: \(x(t)=\frac{1}{3}t^{3}-\frac{3}{2}t^{2}+2t+5\)
d) At what time is the particle closest to the origin (x=0)?
Answer/Explanation
Ans: 𝑥′(𝑡) = 𝑡2 − 32 − 2 = 0
→ (𝑡 − 2)(𝑡 − 1) = 0, 𝑡 = 1, 2
There are relative extrema at t = 1 and t = 2
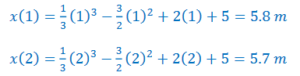
These values must also be compared to the endpoint at t = 0.
𝑥(0) = 5 𝑚
Since the starting position is smaller than the two relative extrema, the initial value is the absolute minimum value of the position.
What accelerates falling objects?
▪ Objects falling toward earth have constant acceleration that is independent of mass:
A free body diagram of an object that is freely falling will only have a single force on it, which is gravity acting downwards:
Using Newton’s 2nd Law (𝐹 = 𝑚𝑎):
![]()
Therefore, any object that is airborne with no other forces on it will experience a constant acceleration of g, where g = 9.81 m/s2 downwards, independent of the object’s mass.
▪ Some “Formulas” *you should know how to derive the following –Time in the air for dropped object:
Consider an object dropped from rest form a height of h. Down is taken as the positive direction since it is the only direction of motion.
Variables: ∆𝑦 = ℎ, 𝑎 = 𝑔, 𝑣𝑖 = 0, 𝑡 =?
Equation that results the variables:\(\Delta y=v_{i}t+\frac{1}{2}at^{2}\)
Solving for time: 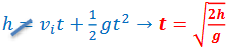
–Time in the air for an object thrown up:
For the entire motion of an object that is thrown up from a certain height, and lands at the same height, the vertical displacement is zero.
Additionally, if there is no air resistance, the object will have the same speed as it launch (but opposite sign) when it hits the ground (due to conservation of energy).
Variables: ∆𝑦 = 0, 𝑎 = −𝑔, 𝑣𝑖 = 𝑣, 𝑣𝑓 = −𝑣 𝑡 =?
Equation that results the variables: 𝑣𝑓 = 𝑣𝑖 + 𝑎𝑡
Solving for time: ![]()
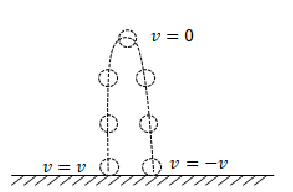
–Velocity at max height:
At max height, the object’s velocity is switching direction from upwards to downwards, so there is a short instant at max height where the velocity is instantaneous equal to zero.
*The speed is only zero in the y–direction, an object with a horizontal component of velocity will stay have that horizontal component at max height.
–Max height:
Variables: 𝑣𝑖 = 𝑣, 𝑎 = −𝑔, 𝑣𝑓 = 0, ∆𝑦 =?
Equation that results the variables: ![]()
Solving for displacement: ![]()
*This is displacement at max height for an object thrown up at initial speed of 𝑣. If a problems asks for “max height”, this value needs to be added to the initial height.
Graphs for an object thrown straight upwards
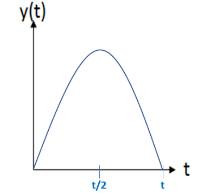
◾Position vs. time graph
*The graph is parabolic since any object in the air with only gravity (a=–g) acting will have a displacement given by \(\Delta y=v_{i}t-\frac{1}{2}gt^{2}\), which is a quadratic function.
*The max height occurs at half the time in the air. The time to max height is t = v/g (where v is the initial y–velocity) and the time to hit the ground is t = 2v/g.
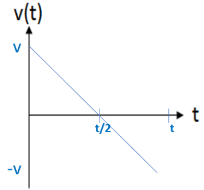
◾Velocity vs. time graph
*The initial final speeds are the same, but the velocities are opposite.
*The velocity switches signs at max height.
*Since the position graph is a quadratic function (and the acceleration is constant), the velocity graph is linear.
Solve problems where air resistance is negligible.
Example A: A ham sandwich is thrown vertically upward at 45 m/s from the roof of a 100 m tall building.
a) What is the maximum height of the sandwich?
Answer/Explanation
Ans: \(v_{i}=45\frac{m}{s}, a= -10\frac{m}{s^{2}}, v_{f}=0, \Delta y=?\)
\({v_{f}}^{2}={v_{i}}^{2}+2a\Delta y\)
\(\Delta y=\frac{-{v_{i}}^{2}}{2a}=\frac{-(45\frac{m}{s})^{2}}{2(-10\frac{m}{s})}=101 m\)
\(y_{max}=y_{i}+\Delta y=100 m + 101m = 201 m\)
b) How long does it take the sandwich to reach the top of the building again?
When the sandwich reaches its initial height again, there is zero displacement in the y–direction.
Answer/Explanation
Ans: \(v_{i}=45 \frac{m}{s}, a = -10\frac{m}{s^{2}}, \Delta y=0 m\)
t = ?
\(\Delta y^{2}=v_{i}t+\frac{1}{2}at^{2}\)
\(-v_{i}=\frac{1}{2}at\Rightarrow t=\frac{-2v_{i}}{a}=\frac{-2(45\frac{m}{s})}{-10 \frac{m}{s^{2}}}=9s\)
c) With what speed does the sandwich hit the ground?
The sandwich will go up and then back down again, but only the downward displacement of 100 m needs to be accounted for when using kinematic equations.
Answer/Explanation
Ans: \(v_{i}=45 \frac{m}{s}, a = -10\frac{m}{s^{2}}, \Delta y = -100 m\)
vf = ?
\({v_{f}}^{2}={v_{i}}^{2} + 2 a\Delta y\)
\(\Rightarrow v_{f}=\sqrt{(45 \frac{m}{s})^{2}+2(-10 \frac{m}{s^{2}})(-100m)}=63 \frac{m}{s}\)
Example B: An arrow is shot directly upward. On its way up, it has a velocity of 25 m/s at a point when it is 50 m above the ground.
a) How long after this will the arrow hit the ground?
Answer/Explanation
Ans: \(v_{i}=25 \frac{m}{s}, a = -10\frac{m}{s^{2}}, \Delta y = -50 m\)
t = ?
\(\Delta y = v_{i}t+ \frac{1}{2}at^{2}\)
\(-50 = 25t- 5t^{2}\)
t = 6.5 s – 1.5s
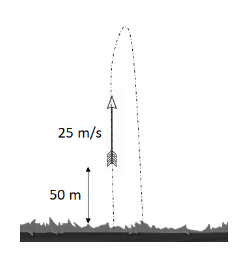
When using kinematics, 2 solutions for time are found. Obviously, the positive time is when the object hits the ground. The negative solution of –1.5 s means that the arrow was ground level 1.5 s ago, which is the time of it being fired.
b) With what speed was the arrow launched upward?
For this problem, 25 m/s is the final velocity and the initial velocity is taken as when the arrow was fired at ground level.
Answer/Explanation
Ans: \(v_{f}=25 \frac{m}{s}, a = -10\frac{m}{s}, \Delta y = 50 m\)
vi = ?
\({v_{f}}^{2}={v_{i}}^{2} + 2 a\Delta y\)
\(v_{i}=\sqrt{{v_{f}}^{2}-2a\Delta y}=\sqrt{(25\frac{m}{s})^{2}-2(-10\frac{m}{s})(50m)}=40 \frac{m}{s}\)
Solve problems with drag.
Example C: Jar Jar Binks, with a mass of M, is dropped form an airplane high above the ground. The vertical force vs. time on Jar Jar can be given by: 𝐹(𝑡) = 𝑚𝑔 − 𝑘𝑣, where k is a constant known as the drag coefficient. The drag force (kv) acts against the motion of the falling object, and increases with speed. Therefore, this force increases as the object falls. At some point, called terminal velocity, the speed will be sufficient so that the upward force of drag equals the downward force of gravity, leading to zero net force, and therefore constant speed since there is zero acceleration.
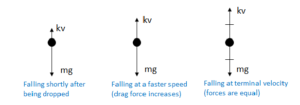
a) Find Jar Jar’s terminal velocity.
Answer/Explanation
Ans: Using Newton’s 2nd Law : \(ma = mg=kv\rightarrow m\frac{dv}{dt}=mg – kv\)
At terminal velocity, 𝑣𝑇 , the speed does not change, \(\frac{dv}{dt}=0\)
\(m(o)=mg-kv_{T}\rightarrow 0 = mg – kv_{T}\rightarrow mg=kv_{T}\rightarrow v_{T}=\frac{mg}{k}\)
b) Solve for Jar Jar’s speed as a function of time.
Answer/Explanation
Ans: Function for dv/dt as a function of v: \(m\frac{dv}{dt}=mg-kv\)
Multiply both sides by –1/k (this makes the integration easier): \(-\frac{m}{k}\frac{dv}{dt}=v-\frac{mg}{k}\)
Separate the variables: \(\frac{dv}{v-\frac{mg}{k}}=-\frac{k}{m}dt\)
Set up bounds and integrate both sides. The velocity starts at 0 (since the object is dropped from rest) and goes to some velocity 𝑣(𝑡) and time t. The time starts at t =0 and goes until some variable time t.
\(\int_{0}^{v(t)}\frac{dv}{v-\frac{mg}{k}}=\int_{0}^{t}-\frac{k}{m}dt\)
The integration for velocity is simple using u substitution with \(u = v – \frac{mg}{k}and du = dv\)
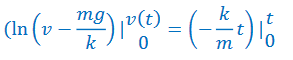
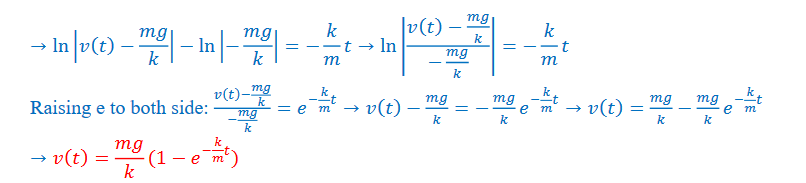
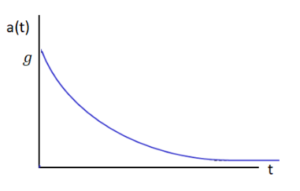
Since mg/k is equal to the terminal velocity, 𝑣𝑇 , this can also be written as \(v(t)=v_{T}(1-e^{-\frac{k}{m}t})\) This function shows that the velocity starts at zero and asymptotically approaches it terminal velocity:

Taking the derivative of v(t) gives the acceleration function:
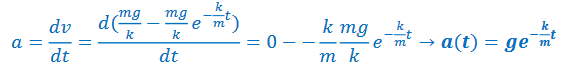
This function shows that the acceleration starts at the acceleration due to gravity, g, and asymptotically approaches zero acceleration: