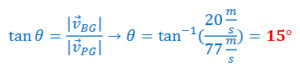What are vector components?
A vector is a quantity with both direction and magnitude. Vectors can be represented by an arrow, with the arrow pointing in the appropriate direction of the quantity and the length of the arrow representing the magnitude of the quantity.
A position vector, 𝑟⃗ , has an x and y components (both x and y can be functions of time). Position vectors in are typically drawn from the origin to the point that represents the position of the particle. There are different common notations for vectors:
![]()
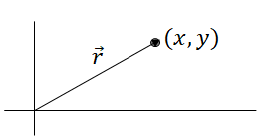
Dot Product
▪ For two vectors \(\vec{a}\) and \(\vec{b}\) : The dot product, or scalar product, between two vectors is a mathematical operation where two vectors are multiplied to get a scalar result.
➢ The dot product can be found by multiplying the magnitudes of the vectors by the cosine of the angle between them: \(\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}| cos\theta \)
➢ The dot product can also be found by adding products of corresponding components. Suppose \(\vec{a}=<a_{1},a_{2}> and \vec{b}=<b_{1},b_{2}>: \vec{a}\cdot \vec{b}=a_{1},b_{1}+a_{2},b_{2}\)
▪ \(\vec{a}\cdot \vec{b}\) is calculated by adding the product of corresponding components:
▪ If \(\vec{a}\cdot \vec{b}\) = 0, the vectors are perpendicular.
Use vector components of kinematic quantities.
Position Vectors
𝑟⃑ = 𝑥𝑖̂ + 𝑦𝑗̂ is a vector that represents the position of a particle. The tail is at the origin and the head is at the point (x,y). The particle itself is located at the head of the vector.

Velocity Vectors
▪ Average Velocity: The average velocity can be found simply by finding change in positive over time.
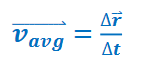
▪ Instantaneous Velocity:
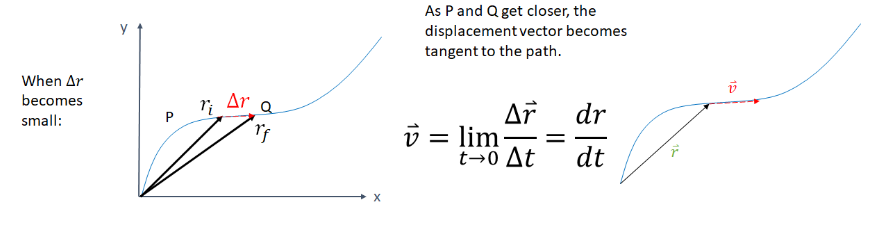
▪ Relationship between 𝑣⃑ and its components:
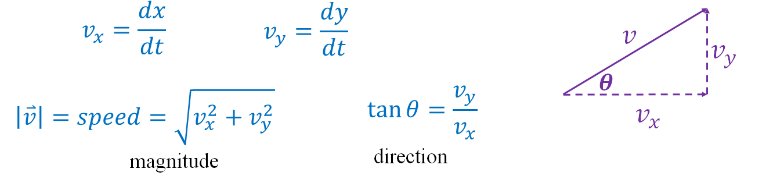
Example A: An object’s position can be given by the equation 𝑟⃑ = (2𝑡)𝑖̂ + (5 − 𝑡)𝑗̂ .
a) What is the location of the object at time t = 4.0 s?
Answer/Explanation
Ans: \(\vec{r}(4)=(2)(4)\hat{i}+(5-4)\hat{j}\Rightarrow \vec{r}(4)=(8\hat{i}+\hat{j})m\)
b) What is the velocity of the object at time t = 4.0 s?
Answer/Explanation
Ans: \(\vec{v}=\frac{d\vec{r}}{dt}=\frac{d(2t)}{dt}\hat{i}+\frac{d(5-t)}{dt}\hat{i}\Rightarrow \vec{v}=2\hat{i}-\hat{j}\)
\(\vec{v}(2)=2\hat{i}-\hat{j}\)
c) What is the minimum distance between the object and the origin?
Answer/Explanation
Ans: First, the position function needs to be used to find the distance with the distance formula.
\(Distance = \sqrt{(2t)^{2}+(5-t)^{2}}=\sqrt{4t^{2}+25-10t+t^{2}}\)
\(\Rightarrow Distance = \sqrt{5t^{2}-10t+25}\)
It would be difficult to find the derivative of the distance in order to maximize the distance function.
However, it’s easy to maximize the value under the radical.
D’ = 10t – 10 = 0 ⇒ t = 1
A relative extrema occurs at t = 1; this also needs to be compared to the starting distance.
\(Distance(1) = \sqrt{5(1)^{2}-10(1)+25}=\sqrt{20}\)
\(Distance(0) = \sqrt{25}=\5\)
d) When is the object’s velocity perpendicular to its position?
Answer/Explanation
Ans: This occurs when the dot product is zero.
\(\vec{r}\cdot \vec{v}=(2t)2+(5-t)(-1)=4t-5+t=5t-5\)
\(\vec{r}\cdot \vec{v}\cdot =5t-5=0\)
⇒t = 1a
Acceleration
▪ Average Acceleration: \(\vec{a_{avg}}=\frac{\Delta \vec{v}}{\Delta t}\)
Example B: The HMS Boaty McBoatface travels at 10.0 m/s, 20° W of N. Its final velocity, 10.0 s later, is 12.0 m/s, 50° W of N. What is its average acceleration?
Answer/Explanation
Ans:
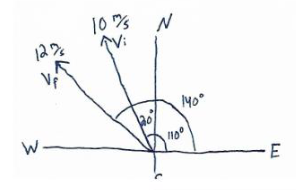
\(a_{x}=\frac{12 cos 140^{0}-10 cos 110^{0}}{10s}=-.58s\)
\(a_{y}=\frac{12 sin 140^{0}-10 sin 110^{0}}{10s}=-.17s\)
\(\vec{a}=(-.58\hat{i}-.17\hat{j})\frac{m}{s^{2}}\)
▪ Instantaneous Acceleration: the limit of the average acceleration as the change in time becomes small:
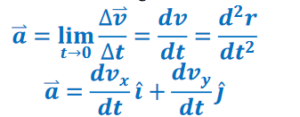
Example C: An object has an acceleration given by 𝑎⃑ = (3𝑡)𝑖̂ + (4 − 2𝑡2)𝑗̂ . The object is rest at the origin at time t =0 s. Find the velocity and position vectors.
Answer/Explanation
Ans: \(\vec{v}=\int \vec{a}dt=\left ( \frac{3}{2}t^{2} \right )\hat{i}+\left ( 4t-\frac{2}{3}t^{3} \right )\hat{j}\)
\(\vec{r}=\int \vec{v}dt=\left ( \frac{1}{2}t^{3} \right )\hat{i}+\left ( 2t^{2}-\frac{1}{6}t^{4} \right )\hat{j}\)
*Since the object has initial conditions are 𝑣(0) =< 0,0 > and 𝑥(0) =< 0,0 >, there are no constants of integration.
Example D: Tired of catching yet another Pidgey, Youngster Joey throws it from the origin with initial velocity
𝑣⃑ = (2)𝑖⃑ + (10)𝑗⃑ . The Pidgey has acceleration 𝑎⃑ = (12𝑡2)𝑖̂ + (−6𝑡)𝑗̂ .
a) What is the maximum height reached by the Pidgey?
Answer/Explanation
Ans: First the functions for velocity and position need to be found.

\(\vec{v}=\int \vec{a}dt=(4t^{3}+2)\hat{i}+(-3t^{2}+10)\hat{j}\)
\(\vec{r}=\int \vec{v}dt=(t^{4}+2t)\hat{i}+(-t^{3}+10t)\hat{j}\)
To find the max height, only the y–component of the position function needs to be maximized.
\(y(t)=-t^{3}+10t\)
\(y'(t)=-3t^{2}+10\Rightarrow -3t^{2}+10=0\)
\(t=\sqrt{\frac{10}{3}}, -\sqrt{\frac{10}{3}}\)
\(y\left ( \sqrt{\frac{10}{3}} \right )=-\left ( \sqrt{\frac{10}{3}} \right )^{3}+10\left ( \sqrt{\frac{10}{3}} \right )=12.2 m\)
b) How far does the Pidgey land from the origin?
To find the final distance of the origin, the x component of position needs to be found when the y position again becomes zero after t = 0.
Answer/Explanation
Ans: \(y(t)=-t^{3}+10t=0 \Rightarrow t^{3}=10t\)
\(t=0, -\sqrt{10},\sqrt{10}\)
\(x(\sqrt{10})=(\sqrt{10})^{4}+2(\sqrt{10})=106 m\)
How does the velocity of a projectile change during its path of motion?
▪ Projectile – An object that is given some initial velocity and acted upon only by gravity. If there is non– zero horizontal component of velocity, the path of a projectile is a parabola.
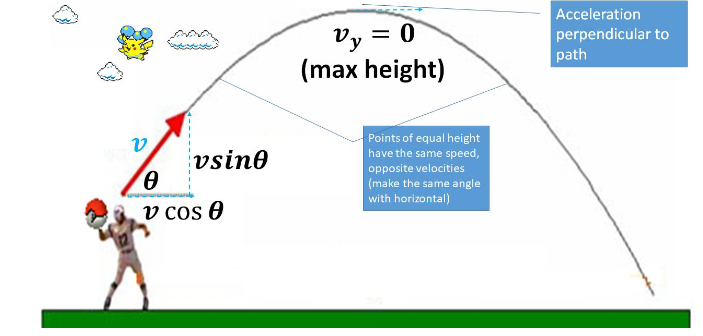
▪ The x and y components of motion are mostly considered separately:
- x–direction: No horizontal force, so no acceleration occurs.

- y–direction: Gravity acts directly downward at all times (free fall)
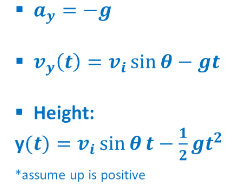
- Vector notation:
Example A: What assumptions are made in order for the formulas given above to be valid?
Answer/Explanation
Ans: ➢ Acceleration due to gravity, g, is constant with height.
➢ No air resistance is present while the projectile is in flight.
Solve for kinematic quantities in projectile problems.
Example B: A projectile is launched from ground level with initial velocity 𝑣 at angle 𝜃 above the horizontal.
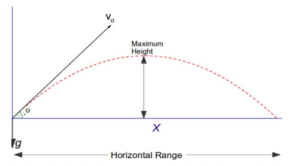
a) Calculate the maximum height reached by the projectile.
Answer/Explanation
Ans: y- direction :
\(v_{i}=vsin\theta , a = -g, v_{f}=0, \Delta y=?\)
\({v_{f}}^{2}={v_{i}}^{2}+2a\Delta y\Rightarrow \Delta y=\frac{{v_{f}}^{2}-{v_{i}}^{2}}{2(-g)}\)
\(\Rightarrow \Delta y=\frac{v^{2}sin\theta }{2g}\)
b) Find the time the projectile is in the air.
Answer/Explanation
Ans: y- direction :
\(v_{i}=vsin\theta , \Delta y = 0, v_{f}=-vsin\theta , a=-g, t=?\)
\(v_{f}=v_{i}+at \Rightarrow t=\frac{v_{f}-v_{i}}{a}=\frac{-vsin\theta -vsin\theta }{(-g)}\)
\(\Rightarrow t = \frac{2sin\theta }{g}\)
c) Find the horizontal range of the projectile.
Answer/Explanation
Ans: x- direction :
\(\Delta x=v cos \theta t\)
\(\Delta x=v cos \theta \left ( \frac{2vsin\theta }{g} \right )=\frac{v^{2}2sin\theta cos\theta }{g}\) *2 sin θ cos θ = sin 2θ
\(\Delta x=\frac{v^{2}sin2\theta }{g}\)
d) What numerical value of 𝜃 will allow the projectile to reach its maximum horizontal range?
Answer/Explanation
Ans: The function for ∆𝑥 is maximized when 𝜽 = 𝟒𝟓°
Example C: A ball rolls off a table that is a height ℎ above the ground. It travels a distance 𝑥 horizontal while it is in the air.
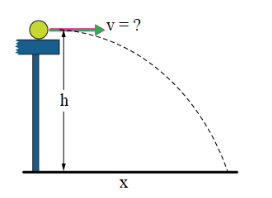
a) How long is the ball in the air?
Answer/Explanation
Ans: y- direction :
\(v_{i}=0, a = -g, \Delta y=-h, t =?\)
\(\Delta y=v_{i}t+\frac{1}{2}at^{2}\Rightarrow \Delta y\frac{1}{2}at^{2}\Rightarrow t=\sqrt{\frac{2\Delta y}{a}}\Rightarrow t=\sqrt{\frac{2h}{g}}\)
b) With what speed does the ball roll off the table?
Answer/Explanation
Ans: x– direction :
\(\Delta x=v_{x}t\Rightarrow v_{x}=\frac{\Delta x}{t}=\frac{x}{\sqrt{\frac{2h}{g}}}\Rightarrow v=x\sqrt{\frac{g}{2h}}\)
Example D: In a typical fit of rage, Philip throws his physics textbook off a cliff at angle of 30° above the horizontal at a velocity of 10 m/s. It lands 100 m from the base of the cliff.
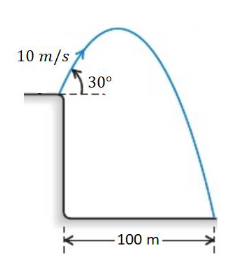
a) How long is the textbook in the air?
Answer/Explanation
Ans: x– direction : use x-dir to find t since Δx is known
\(\Delta x=vcos \theta t\Rightarrow t=\frac{\Delta x}{vos\theta }=\frac{100 m}{ 10 cos 30 \frac{m}{s}}=11.5s\)
b) How high is the cliff?
Answer/Explanation
Ans: y- direction :
\(v_{i}=10 sin 30 = 5\frac{m}{s}, a = -10 \frac{m}{s^{2}}, t=11.5s, \Delta y=?\)
\(\Delta y=v_{i}t+\frac{1}{2}at^{2}=(5\frac{m}{s})(11.5s)+\frac{1}{2}(-10 \frac{m}{s^{2}})(11.5s)^{2}\)
\(\Delta y=-6.04m\)
c) With what velocity (magnitude and direction) does the textbook strike the ground?
Answer/Explanation
Ans: 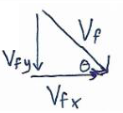
\(v_{fx}=10 cos 30=8.7 \frac{m}{s}(constant)\)
\(v_{fy}=v_{iy}+at=10 cos 30+(-10\frac{m}{s})(11.5s)=-110\frac{m}{s}\)
\(v_{f}=\sqrt{(8.7\frac{m}{s})^{2}+(-110 \frac{m}{s})^{2}}=110.3 \frac{m}{s}\)
\(\theta =tan^{-1}\left ( \frac{v_{fg}}{v_{fx}} \right )=tan^{-1}\left ( \frac{110\frac{m}{s}}{8.7 \frac{m}{s}} \right )=85^{0}\)
Example E: A cannonball is shot at a castle 100 m at angle of 30° above the horizontal. It hits the castle wall at height of 20 m above the ground.
a) What was the launch speed of the cannonball?
Answer/Explanation
Ans: x– direction :
\(\Delta x=vcos\theta t\)
\(t=\frac{\Delta x}{vcos\theta }\)
y- direction :
\(\Delta y=v sin\theta t-\frac{1}{2}gt^{2}\)
\(\Delta y=v sin\theta \left ( \frac{\Delta x}{vcos\theta } \right )-\frac{1}{2}g\left ( \frac{\Delta x}{vcos\theta } \right )^{2}\)
\(\Delta y=\Delta xtan\theta -\frac{\Delta x^{2}}{2gv^{2}cos^{2}\theta }\)
\(20=100tan30^{0} -\frac{(100)^{2}}{v^{2}cos^{2}30 }\)
v = 18.8 m/s
b) How long is the cannonball in the air?
To solve this question, solve for an expression for time in one direction and plug that expression for time into the other direction.
Answer/Explanation
Ans: \(t=\frac{\Delta x}{vcos\theta }=\frac{100m}{18.8 cos30\frac{m}{s}}=6.1s\)
What is an inertial reference frame?
Objective: Analyze the motion of an object relative to a moving medium.
▪ Frame of reference – A coordinate system fixed to a single point. If the point has a fixed position, it is an inertial reference frame.
▪ Addition of vectors is used when analyzing relative motion.
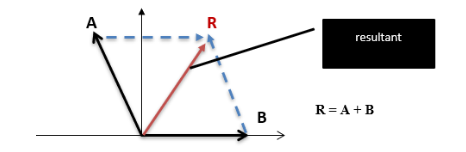
Example: Suppose the velocity of a plane relative to the air is 𝑣𝑃𝐴 and the velocity of the air relative to the ground is 𝑣𝐴𝐺 , then the velocity of the plane relative to the ground is the addition of these two vectors:
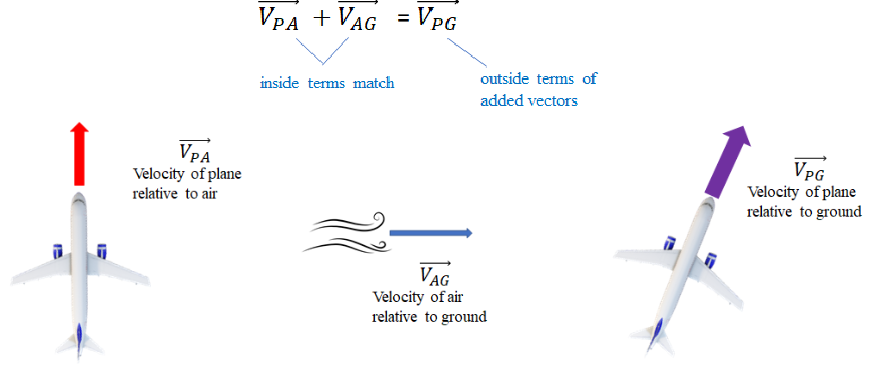
Example A: A pilots wants to fly due north. The speed of the plane relative to the air is 200 km/h and the air blows due east at 60 km/h.
a) In which direction should the plane head?
Answer/Explanation
Ans: 
b) How fast does the plane travel relative to the ground?
Answer/Explanation
Ans: 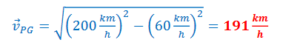
The instruments on the airplane will report the magnitude and direction of \(\vec{v_{PA}}\) , the values relative to the air.
Example B: An airplane drops a bomb on a target. At one particular instant, the bomb is falling at a rate of 20 m/s directly below the airplane. An observer on the ground sees the bomb moving towards the ground at an angle with a speed of 80 m/s.
a) How fast is the airplane flying with respect to the ground?
Answer/Explanation
Ans: 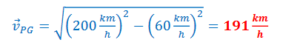
b) What angle does the bomb make with the ground the airplane’s path?
Answer/Explanation
Ans: