What does a force do?
▪ Kinematics – Study of motion without regard to forces causes it.
▪ Dynamics – Study of motion and the forces causing the motion.
▪ Contact Force – A push or pull (the object exerting the force makes contact with the object it exerts the force onto.
▪ Forces are a vector quantity. Forces can be represented by specifying their components:
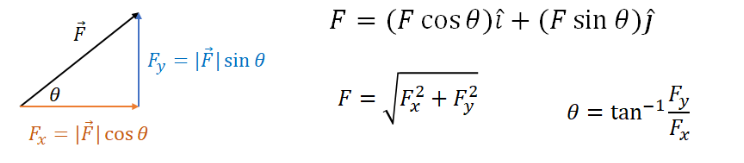
▪ The resultant is the vector sum of all forces acting on a body. When multiple forces act, the forces produce the same result as a single force equal to the vector sum of the forces. The resultant force can be found by adding components or law of cosines (for two vectors only).
Example A: Find the resultant of adding the two forces.
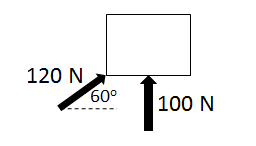
Answer/Explanation
Ans: 𝐹𝑥 = (120 cos 60° + 0) = 60 𝑁
\(F_{y}=(120 sin 60^{0}+100) = (60\sqrt{3}+100)N\)
\(F=(60)\hat{i} + (60\sqrt{3}+100)N\)
Newton’s Laws
▪ Newton’s First Law: \(If \sum \vec{F}=0, a = 0.\)
*Inertia is the tendency of an object to resist acceleration.
▪ Newton’s Second Law: \( \sum \vec{F}=m\hat{a}\)
A force causes an acceleration in the direction of the force. Mass resists force.
▪ Newton’s Third Law: Every action has equal and opposite reaction.
*A single isolated force is not possible.
Example B: A particle of mass 𝑚 has a velocity given by 𝑣(𝑡) = 10 − 2𝑡2. Determine an expression for the force on the particle as a function of time.
Answer/Explanation
Ans: \(F = ma = m\frac{dv}{dt}\)
\(\rightarrow F = m\frac{d(10-2t^{2})}{dt}=m(-4t)\)
→ 𝑭(𝒕) = −𝟒𝒎𝒕
Example C: A man ties a rope to a box and pulls the box across the floor with the rope with increasing velocity. Identify all the action–reaction pairs. Apply F=ma for all three directions.

Answer/Explanation
Ans: Box Action–Reaction Pairs: FTension and FFriction
Man Action–Reaction Pairs: FTension and FFriction
*Notes on the forces
➢ FGravity – This is the force of weight, pulling the box/man down to the ground.
➢ FNormal – When you push on a surface, the surface pushes back. This is called a normal force.
*Common Physics Misconception* Gravity and Normal force are not action–reaction pairs since gravity is a force between the center of mass of the object and the Earth’s center of mass. The normal force acts only at the point of contact. This is will explored more later in Physics 1.
➢ FTension: A pulling force in a rope is called tension. This force pulls the box forward, but tries to pull the man backwards. Think about tug of war, the rope pulls on both sides.
➢ FFriction for the Box: The box is sliding, so friction resists this sliding motion.
➢ FFriction for the Man: When you walk, you push back on the ground with your foot. Friction acts against this pushing backward force, pushing you forward as a result. This is why you can’t walk well on ice; there’s no friction to push back on the ground.
*Newton’s Laws are only valid in inertial reference frames. An inertial reference frame is a set of coordinate axes attached to a body with a constant state of motion (not acceleration). If a reference frame is acceleration, Newton’s Laws do not apply.
What does a force do?
Review: Drawing a Free Body Diagram (FBD)!
▪ Represent each object as having all its mass concentrated at a single point. This is possible since this section only deals with translational motion, and not rotation.
▪ Draw a labeled arrow to represent each force acting on the object. The arrow indicates the force’s direction and the length is proportional to the magnitude of the direction.
▪ Only draw the forces as they act on an “official” FBD response. It is useful to separate forces into components in pseudo–free body diagram, but do not include when a question asks for a FBD.
▪ Set the vector sum of the forces (that act in the direction of motion) equal to mass times acceleration. If the system is in equilibrium, the vector sum will be zero.
Tension
Example A: Given the mass supported by three ropes as shown in the diagram, find the tension in each rope.
Any problem involving F=ma must be started with a free–body diagram:
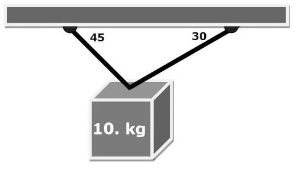
*A free–body diagram does not include components.
*When solving, the x and y directions will be considered separately.
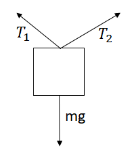
Answer/Explanation
Ans: \(\sum F_{x}=0=T_{2}cos30^{0}-T, cos 45^{0}\)
\(T_{1}=T_{2}\frac{cos 30}{cos 45}=\frac{\sqrt{6}}{2}T_{2}\)
\(\sum F_{y}=0=T_{1}sin 30 + T_{2}sin 45 – mg \)
\(\Rightarrow \frac{\sqrt{6}}{2}T_{2}sin 30 + T_{2}sin 45 = mg \)
\(\Rightarrow T_{2}\left ( \frac{\sqrt{6}}{4}+\frac{\sqrt{2}}{2} \right ) = (10 kg)(10 \frac{m}{s^{2}})\)
\(\Rightarrow T_{2}=76 N\)
\(\Rightarrow T_{1}=(76 N)\left ( \frac{\sqrt{6}}{2} \right )=93N\)
The previous examples assume there was no mass in the ropes, which is a common assumption in AP Physics.
If a rope has mass, the part of the rope supported more of its mass have higher tension (the closer to the point the rope is being pulled will have more tension). The example below demonstrates this.
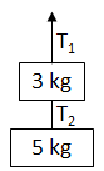
Example B: The system shown below accelerates upward at 2.0 m/s2. Find the tension in each rope.
Answer/Explanation
Ans: T1 > T2 since T1 has to pull more weight. Since both blocks move together, the acceleration for each has to remain the same.
T1 pulls a total mass of 8 kg so 𝑚𝑎 = 𝑇1 − 𝑚𝑔 → 𝑇1 = 𝑚𝑎 + 𝑚𝑔
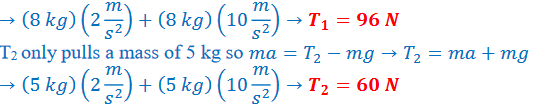
Elevators
▪ When at rest or moving at constant velocity in an elevator, a scale would give a normal reading.
▪ If an elevator accelerates upward (moving up and speeding up or moving down and slowing down) the elevator will push up on the rider, causing them to push down, making apparent weight more.
▪ If an elevator accelerates downward (moving down and speed up or moving up and slowing down), apparent weight will be less. (If free fall, apparent weight is zero).
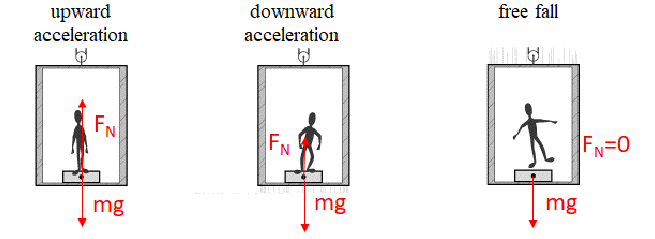
The weight you feel yourself weighing, or “apparent weight” is based on the normal force. The relationship between normal force and weight on an accelerating elevator is given below:
∑ 𝐹 = 𝑚𝑎 = 𝐹𝑁 − 𝑚𝑔 → 𝐹𝑁 = 𝑚𝑎 + 𝑚𝑔
𝑭𝑵 = 𝒎(𝒂 + 𝒈)
➢ If acceleration is up (going up and speeding up or going down and slowing down) : Apparent weight is greater than mg
➢ If acceleration is down (going down and speed up or going up and slowing down): Apparent weight is less than mg.
➢ If acceleration is zero: Apparent weight is equal to mg.
➢ If acceleration is g (free fall): Apparent weight is zero.
Friction
▪ Normal force – perpendicular force applied by a surface in contact with an object.
▪ Frictional force – parallel force exerted on an object by a surface that resists motion.
▪ The force of friction proportional to the normal force:
𝐹𝑓 𝛼 𝜇𝐹𝑁
The pressing force between the two surfaces in contact, which is the normal force FN, increases friction.
Friction is also affected by the property of materials in contact. The material and roughness of surfaces in contact determines the value of 𝜇.
▪ Static friction:
𝐹𝑓 ≤ 𝜇𝑠𝐹𝑛
*Static friction is only as large as it needs to be to stop motion (only cancels out applied force; if it can’t cancel out applied force, kinetic friction acts)
▪ Kinetic friction : When force becomes great enough to over static friction, an object being pushed/pulled will begin to slide. At this point, kinetic friction acts:
𝑭𝒇 = 𝝁𝒌𝑭𝒏
*always less than static friction
Example D: For the block being pulled shown on the right, the coefficient of sliding friction is 𝜇𝑠 and the block is pulled at constant speed on a constant horizontal surface. A force acts an angle 𝜃 above the horizontal. What is the magnitude of 𝐹?
Free Body Diagram
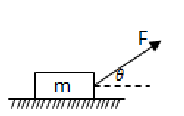
Answer/Explanation
Ans: 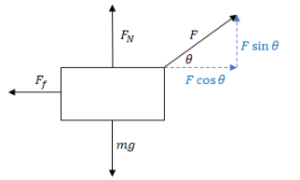
The normal force will be needed when using friction. Since there is an upward force pulling up on the block, the normal force will be less than the block’s weight since the normal force does not have to counteract all the block’s weight. The normal force can be found by setting the sum of forces in the y–direction to zero.
\(\sum F_{y}=0=F_{N}+F_{sin\theta }-mg\)
\(\Rightarrow F_{N}=mg-F_{sin\theta}\)
*If the force was directed downward, the normal force would be 𝑚𝑔 + 𝐹 sin 𝜃
The x–direction can now be considered to solve for F. Since the block moves at constant speed, the forces in the horizontal direction add to zero.
\(\sum F_{x}=F_{cos\theta }-F_{f}=0\) (constant speed)
\(\Rightarrow F_{cos\theta }=\mu F_{n}\Rightarrow F_{cos\theta }=\mu (mg-F_{sin\theta })\)
\(\Rightarrow F_{cos\theta }+\mu F_{cos\theta }=\mu mg\Rightarrow F(cos\theta +\mu sin\theta )=\mu mg\)
\(F = \frac{\mu mg}{cos\theta +\mu sin\theta }\)
▪ When an object is on an incline, the forces acting on it are broken up into components:
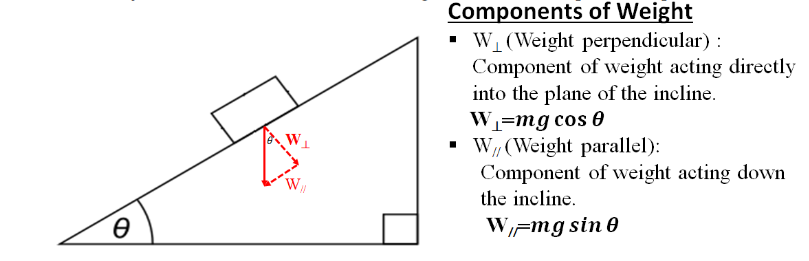
Example E: Consider an incline as shown with a block of mass 𝑚, and coefficients of friction 𝜇𝑠 and 𝜇𝑘.
a) What is the maximum angle for which the block does not slide down the incline?
Answer/Explanation
Ans:
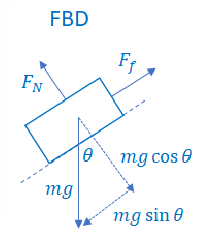
\(\sum F_{f}=0=mgsin\theta -F_{f}\)
\(\Rightarrow 0=mgsin\theta -M_{s}mgcos\theta \)
\(\Rightarrow M_{s}=\frac{mgsin\theta }{mgcos\theta }=tan\theta \)
\(\theta =tan^{-1}\mu _{s}\)
b) At the angle from part a), the block starts to slide down the incline. At what rate does the block side?
Answer/Explanation
Ans: \(\sum F_{“}=ma=mgsin\theta -\mu _{k}mgcos\theta \)
\(\Rightarrow a = gsin(tan^{-1}\mu _{s})-\mu _{k}gcos(tan^{-1}\mu _{s})\)
Example F: Mass 𝑚 is pushed up the incline by a horizontal force 𝐹. The incline makes an angle of 𝜃 with the horizontal and the coefficient of sliding friction is 𝜇.
Derive an expression for the magnitude of the force F for which the block will slide up the incline at constant velocity.
Answer/Explanation
Ans: 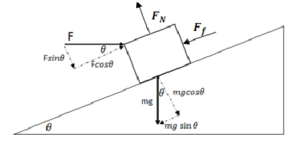
➢ Forces Perpendicular to Incline (out of the incline is defined as the positive direction)
∑ 𝐹⊥ = 𝐹𝑁 − 𝐹 sin 𝜃 − 𝑚𝑔 cos 𝜃 = 0 → 𝑭𝑵 = 𝑭 𝐬𝐢𝐧 𝜽 + 𝒎𝒈 𝐜𝐨𝐬 𝜽
*The normal force has to overcome both the perpendicular component of the block’s weight and the component of F pushing the block directly into the incline.
➢ Forces Parallel to Incline
∑ 𝐹|| = 𝐹 cos 𝜃 − 𝑚𝑔 sin 𝜃 − 𝐹𝑓 = 0
→ 𝐹 cos 𝜃 − 𝑚𝑔 sin 𝜃 − 𝜇𝐹𝑁 = 0 → 𝐹 cos 𝜃 − 𝑚𝑔 sin 𝜃 − 𝜇(𝐹 sin 𝜃 + 𝑚𝑔 cos 𝜃) = 0
→ 𝐹 cos 𝜃 − 𝑚𝑔 sin 𝜃 − 𝜇𝐹 sin 𝜃 − 𝜇𝑚𝑔 cos 𝜃 = 0
→ 𝐹(𝑐𝑜𝑠𝜃 − 𝜇 sin 𝜃) = 𝑚𝑔 sin 𝜃 + 𝜇𝑚𝑔 cos 𝜃 → \(F=\frac{mgsin\theta +\mu mgcos\theta }{cos\theta -\mu sin\theta }\)
Pulleys
Example G: For the pulley shown on the right, m1>m2. Find the acceleration of the system.
Answer/Explanation
Ans: Pulley problems can be solved by looking at the two blocks as a single system. The tension of the rope is an internal force. Internal forces do not affect the motion of a system; only external forces can change the velocity of a system.
Consider the pulley shown with m1>m2. The weight of block two will act in the direction of motion and will therefore be the positive force. The weight of the heavy block will be a positive force since it drags the system in the direction of motion while the lighter’s block weight is a negative force since it opposes the motion of the system.
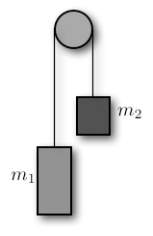
\(a=\frac{total force acting on two block system}{total mass of two block system}\)
\(a=\frac{m_{1}g-m_{2}g}{m_{1}+m_{2}}\)
Example H: For the system shown, m < M. The coefficient of sliding friction between m and the inclined plane is 𝜇, and 𝜃 = 30°. Assume that M is sufficient so that it falls down, dragging m behind it.
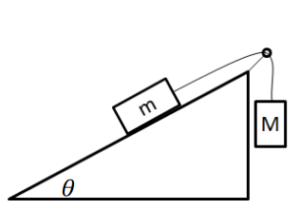
a) Find the magnitude of the acceleration of M.
Answer/Explanation
Ans: 
➢ Forces in the direction of system’s motion (positive forces): 𝑀𝑔
➢ Forces opposing direction of system’s motion (negative forces): 𝐹𝑓, 𝑚𝑔 sin 𝜃
*The tension forces are internal and do not affect the system’s motion.
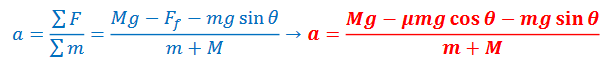
b) Find the tension in the rope.
Answer/Explanation
Ans: To find the tension, the equation for either block can be used:
m: 𝑚𝑎 = 𝑇 − 𝜇𝑚𝑔 cos 𝜃 − 𝑚𝑔 sin 𝜃
M: 𝑀𝑎 = 𝑀𝑔 − 𝑇
Either equation can be used to solve for T; the second one is easier:
𝑇 = 𝑀𝑔 − 𝑀𝑎 → ![]()