What is centripetal acceleration?
Curved paths – For an object on a curved path, the acceleration has normal (perpendicular) and tangent (parallel) components.
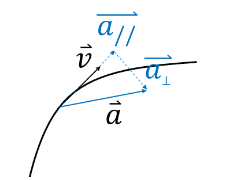
- When the acceleration is parallel to the path of motion: 𝑎// is the part of 𝑎⃑ that acts to change speed; the tangential acceleration.
- When the acceleration is perpendicular to the path of motion: 𝑎⊥ is the part of 𝑎⃑ that acts to change direction, the radial acceleration
Average and instantaneous velocity
▪ Circular Motion – Motion in with a constant perpendicular component to acceleration.
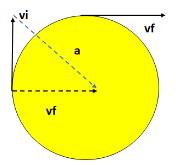
Magnitude of centripetal acceleration is given by: \(a_{c}=\frac{v^{2}}{r}\)
A centripetal acceleration only acts to change the direction of the velocity to keep the object in a circle. If the centripetal acceleration suddenly stops, the object will fly off tangent to the circle; this phenomenon is known as the centrifugal force.
Example A: If an acceleration exists in uniform circular motion, then why do objects move at constant speed?
Answer/Explanation
Ans: Acceleration has no tangential component, so only direction is changing. In uniform circular motion, only the direction of the object changes to stay in a circle.
*If speed is not constant, then the acceleration must have a tangential component.
Example B: A car has a constant acceleration of 0.300 m/s2 parallel to the roadway. The car passes over a rise in the roadway such that the top of the rise is shaped like an arc of a circle of radius 500 m. At the moment the car is at the top of the rise, its velocity vector is horizontal and has a magnitude of 6.00 m/s. What are the magnitude and direction of the total acceleration vector for the car at this instant?
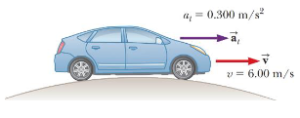
Answer/Explanation
Ans: The tangential acceleration is given: \(a_{||}=.30\frac{m}{s^{2}}\)
The centripetal acceleration can be found using the formula: ![]()
These are both components of the total acceleration vector of the car, so the total acceleration’s magnitude can be found:
![]()
▪ Period: time for one trip around the circular path.

▪ Frequency: number of revolutions per second
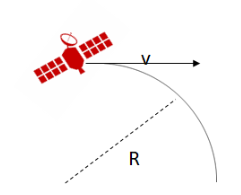
Example C: Suppose that a space probe can withstand the stresses of a 20g acceleration. The craft is moving at a speed of 1/10 the speed of light (c = 3 x 108 m/s). How long would it take to complete a 90 degree turn (1/4 circle) at this rate?
Answer/Explanation
Ans: The maximum acceleration of the rocket is 20g, so the maximum turning radius can be found by setting the centripetal acceleration equal to this value.
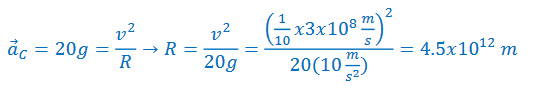
The total distance the rocket travels in the turn is ¼ the circumference of a circle with radius R.
\(distance = \frac{2\pi (4.5\times 10^{12}m)}{4}=7.1\times 10^{12}m\)
Kinematics can be used to find the time. Woah.
\(time=\frac{distance}{speed}=\frac{7.1\times 10^{12}m}{3\times 10^{7}m/s}=75000\pi s=\sim 65 hours\)
Example D: A particle has a position given by 𝑟⃑ = (𝑅 cos 𝜔𝑡)𝑖̂ + (𝑅 sin 𝜔𝑡)𝑗̂ . Determine the following:
a) The equation of the object’s linear motion.
Answer/Explanation
Ans: \(x^{2}+y^{2}=(R cos\theta t)^{2}+(R sin\theta t)^{2}\)
\(\Rightarrow x^{2}+y^{2}=R^{2}(cos^{2}\theta t+sin^{2}\theta t)\)
\(\Rightarrow x^{2}+y^{2}=R^{2}\)
This shows that the function given is for an object traveling in a circle of radius r.
(b) \(\vec{a}(t)\)
Answer/Explanation
Ans: \(\vec{v}(t)=\frac{d\vec{r}}{dt}=-R\omega sin(\omega t)\hat{i}+R\omega cos(\omega t)\hat{j}\)
\(\vec{a}(t)=\frac{d\vec{v}}{dt}=-\omega ^{2}R\omega cos(\omega t)\hat{i}-\omega ^{2}R\omega sin(\omega t)\hat{j}\)
c) The linear acceleration of the particle.
Answer/Explanation
Ans: Linear acceleration \(=|\vec{a}|\)
\(|\vec{a}|=\sqrt{(-\omega ^{2}Rcos(\omega t))^{2}+(-\omega ^{2}Rsin(\omega t))^{2}}\)
\(\Rightarrow |\vec{a}|=\sqrt{\omega ^{4}R^{2}(sin^{2}(\omega t)+cos^{2}(\omega t))}=\omega ^{2}R\)
\(|\vec{a}|=\left ( \frac{V}{R} \right )^{2}R=\frac{v^{2}}{R}\)
This is a rough derivation of the centripetal acceleration formula.
What force keeps moving objects on a circular path?
▪ When an object moves in a circle, it centripetal accelerates keeps changing the direction of velocity to keep it in a circle. By Newton’s second law, a force must cause this acceleration:
∑ 𝐹 =Sum of all forces acting perpendicular to the circular path of motion
Forces in Circular Motion
▪ Do not include “centripetal force” as a force acting on the system when applying ∑ 𝐹 = 𝑚𝑎. Rather, the vector sum of the forces acting on the system equal the centripetal force.
\(\sum F=ma_{c}=\frac{mv^{2}}{r}\)
▪ Some force in the world must cause centripetal force. Common sources are tension, gravity, and friction.
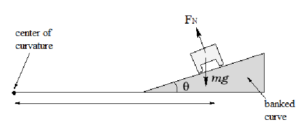
Example A: Banked Curve – Civil engineers generally bank curves on roads in such a manner that a car going around the curve at the recommended speed does not have to rely on friction between its tires and the road surface in order to round the curve. Suppose that the radius of curvature of a given curve is 60 m, and that the recommended
speed is 40 km/hr. At what angle should the curve be banked?
Answer/Explanation
Ans: 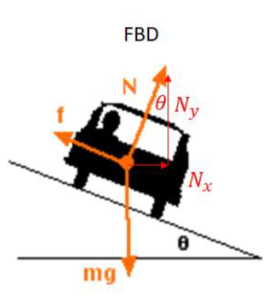
➢ The car is in a horizontal circle. The horizontal component of the normal force keeps the car in a circle.
\(\sum F_{x}=N_{x}\rightarrow Nsin\theta =\frac{mv^{2}}{R}\)
➢ In the vertical direction, normal force cancels out weight so the car does not slide up or down the incline of the curve.
\(\sum F_{y}=N_{y}-mg\rightarrow Ncos\theta-mg =0\)
\(N = \frac{mg}{cos\theta }\)
Substituting the value of normal force from the y–equation into the x–equation:
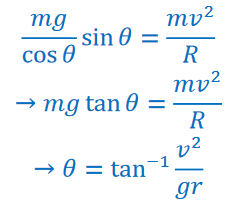
Example B: Gravitron – In the ride “Spindletop” at Six Flags, people stand on the inner wall of a hollow vertical cylinder of radius 3 m. The cylinder starts to rotate and when it reaches 0.5 Hz, the floor at which people are standing drops and the riders remain pinned against the wall. What is the minimum coefficient of static friction so the riders do not drop down?
Answer/Explanation
Ans: 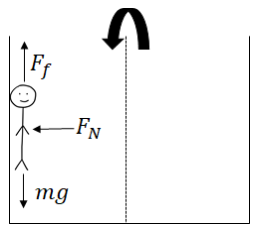
The rider does not slide down the wall due to friction:
𝐹𝑦 = 0 = 𝐹𝑓 − 𝑚𝑔 → 𝜇𝐹𝑁=mg
The normal force on the rider is equal to the centripetal force. \(F_{N} = \frac{mv^{2}}{R}\)
This is not an actual force on the rider, but is caused by an acceleration of the reference the rider is in; this is an example of a fictitious force.
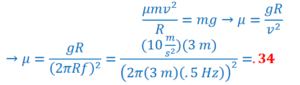
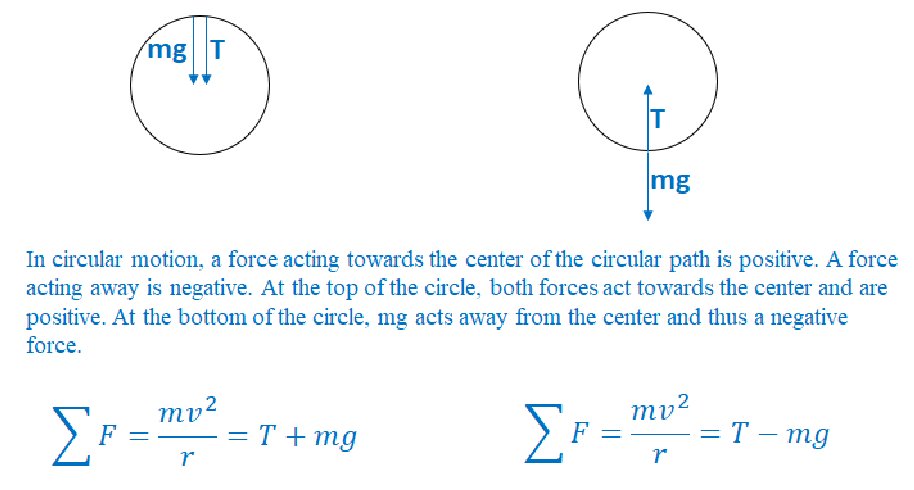
Motion in a Vertical Circle
▪ When an object travels in a vertical circle, uniform circular motion does not occur. Objects travel faster on the way down the vertical circle and slow down when traveling upwards.
At the top of the circle, tension and gravity both act to keep the object in a circle. At the bottom of the circle, gravity tries to bring the object out of the circle, and tension has to both keep the object in a circle and overcome gravity.
▪ Critical speed: Minimum speed the object must have at the top of the loop in order to reach the top.
Think about a mass going around at the end of the string in a circle. The minimum tension the rope can have before going slack and the circular motion ending is T = 0 N.
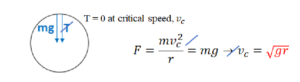
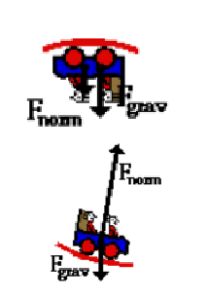
▪ Vertical Loops on Roller Coasters – Finding the normal force between seat/rider.
- *Centripetal force requirement: There must always be an inward force acting on the rider equal to \(\frac{mv^{2}}{r}\)
- Top – Normal Force and gravity both act towards center.
*normal force less than weight
- Bottom – Normal Force acts towards center and gravity acts away.
*normal force greater than weight
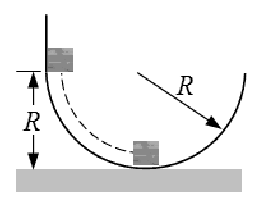
Example D: A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a
frictionless circular hoop of radius R. What is the magnitude of the normal force exerted on the block by the hoop when the block reaches the bottom of the hoop?
Answer/Explanation
Ans: FBD at bottom
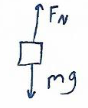 \(\sum F_{y}=\frac{mv^{2}}{R}=F_{N}-mg\)
\(\sum F_{y}=\frac{mv^{2}}{R}=F_{N}-mg\)
Speed at bottom
Vi + ki = vf + kf
mgR = 1/2 mv2
\(V=\sqrt{2gR}\)
\(F_{N}=\frac{mv^{2}}{R}+mg\)
\(F_{N}=\frac{m^{2}gR}{R}+mg\)
\(\Rightarrow F_{N}=3 mg\)
▪ Other Parts of a Vertical Circle (angles)
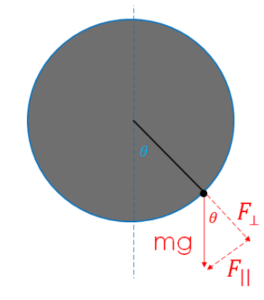
➢ Normal component, 𝐹⊥: Component of weight that acts outward, normal to the circle (affects the direction of the velocity).
𝑚𝑔cos𝜃
➢ Parallel component of weight, 𝐹||: Component of weight that acts tangent to circle (affects the speed of the object).
𝑚𝑔sin𝜃
*Consider the case of a thing on a string in a vertical circle. To find the tension at the point shown in the diagram, the equation would be:
\(\sum F=\frac{mv^{2}}{R}=T-mgcos\theta \)
*The previous equation is only valid for the lower half of the circle, where the weight of the object acts away from the center. In the top half, the equation becomes:
\(\sum F=\frac{mv^{2}}{R}=T+mgcos\theta \)
Example E: A 0.5 kg rock is whirled in a vertical circle. The speed of the rock at the instant shown is 4.0 m/s with R = 1.5 m and 𝜃 = 40°.
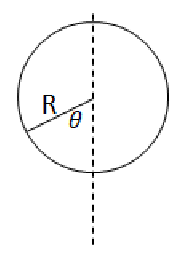
a) What is the magnitude of the rock’s acceleration?
Answer/Explanation
Ans: \(a_{“}=gsin\theta =(10 \frac{m}{s^{2}})sin 40 = 6.4 \frac{m}{s^{2}}\)
\(a_{\perp }=\frac{v^{2}}{R}= \frac{(4 m/s)^{2}}{1.5 m} = 10.7 \frac{m}{s^{2}}\)
\(a=\sqrt{(6.4 m/s^{2})^{2}+(10.7 m/s)^{2}}=12.4 m/s^{2}\)
b) What is the tension in the rope?
Answer/Explanation
Ans: 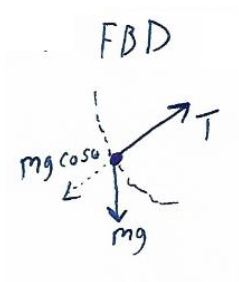
\(\sum F = \frac{mv^{2}}{R}=T-mg cos\theta \)
\(T = \frac{(.5 kg)(4 m/s)^{2}}{1.5 m}=T-mg cos\theta +(.5 kg)(10 m/s^{2})cos 40^{0}\)
T = 9.2 N