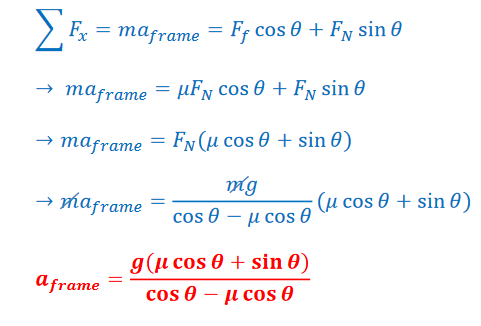What does a force do?
When resistive forces exist, they are often proportional somehow to the object’s velocity, which require setting up a differential equation. Being asked to write a differential equation sounds scary, but in a problem involving forces, this usually just means using Newton’s Second Law:
\(F = m \frac{dv}{dt}\)
Example A: A particle of mass 𝑚 has an initial velocity 𝑣0 and starts at the origin. The force on the particle is given by 𝐹 = −𝑘𝑣2. Find an equation for v(t)
There is no driving force, so the differential equation is simple to solve.
Answer/Explanation
Ans: \(m \frac{dv}{dt}=-kv^{2}\)
First, separate the variables.
\(\frac{dv}{v^{2}}=-\frac{k}{m}dt\)
The bounds for each side need to be set. The velocity starts at v0 and the time starts at 0.
\(\int_{v_{0}}^{v(t)}\frac{dv}{v^{2}}=\int_{0}^{t}-\frac{k}{m}dt\)
Integrate both sides and solve for v(t).
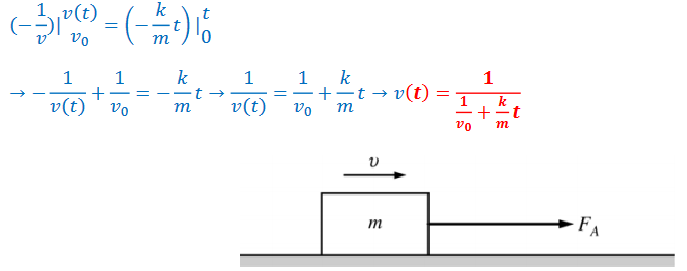
Example B: A box of mass 𝑚 initially at rest is acted upon by a constant applied force of magnitude FA, as shown in the figure above. Friction can be assumed to be negligible, but the box is subject to a drag force of magnitude 𝑘𝑣 where 𝑣 is the speed of the box and 𝑘 is a positive constant. Assuming the box starts from rest, derive an expression for the terminal velocity of the box as a function of time.
Answer/Explanation
Ans: \(m\frac{dv}{dt}=F_{A}-kv\)
Multiply both sides by –1/k to simplify integration
\(-\frac{m}{k}\frac{dv}{dt}=v-\frac{F_{A}}{k}\)
Separate the variables:
\(\frac{dv}{v-\frac{F_{A}}{k}}=-\frac{k}{mk}dt\)
The velocity starts at v and goes to some velocity 𝑣(𝑡) and time t. The time starts at t =0 and goes until some variable time t.
\(\int_{v}^{v(t)}\frac{dv}{v-\frac{F_{A}}{k}}=\int_{0}^{k}-\frac{k}{mk}dt\)
Integration with \(u=v-\frac{F_{A}}{k}\) and 𝑑𝑢 = 𝑑𝑣
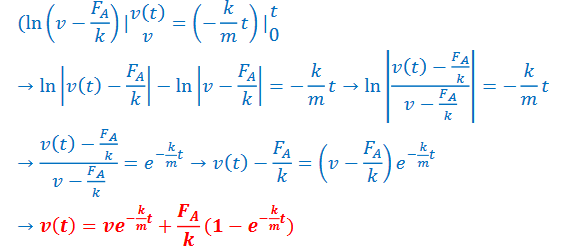
Example C: A rubber ball of mass m is thrown up with speed v0. As the ball is in the air, it is subject to drag The drag force on the ball has magnitude bv2.
a) Draw a free–body diagram of the ball
Answer/Explanation
Ans: i. on the way up and ii. on the way down.
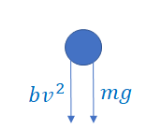
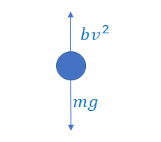
*the drag force will always go opposite direction of motion.
b) Does the ball take long to go i. from the ground to max height or ii. from the max height to the ground?
Justify your answer.
Answer/Explanation
Ans: The ball will take longer to go down. On the way up, both forces act to stop the ball’s upward motion. On the way down, there is opposing forces on the ball. Also, there will be a higher average speed on the way up than the way down since there is energy lost before the ball goes down.
c) Determine an expression for the ball’s terminal velocity.
Answer/Explanation
Ans: \(ma = mg -bv^{2}\rightarrow m\frac{dv}{dt}=mg-bv^{2}\)
At terminal velocity, 𝑣𝑇 , the speed does not change, \(\frac{dv}{dt}=0\)
\(m(0)=mg-bv_{T}^{2}\rightarrow 0=mg-bv_{T}^{2}\rightarrow mg=bv_{T}^{2}\rightarrow v_{T}=\sqrt{\frac{mg}{b}}\)
d) Derive an expression for the velocity of the ball as a function of time on its way down. Assume max height of the ball is t = 0.
\(m\frac{dv}{dt}=mg-bv^{2}\)
\(\frac{m}{b}\frac{dv}{dt}=\frac{mg^{{V_{T}}^{2}}}{b}-v\Rightarrow \frac{m}{b}\frac{dv}{dt}=v{_{T}}^{2}-v^{2}\)
\(\Rightarrow \frac{m}{b}\frac{dv}{dt}=1-\frac{v^{2}}{{v_{T}}^{2}}\)
\(\Rightarrow \int_{0}^{v(t)}\frac{dv}{\frac{v^{2}}{{v_{T}}^{2}}}=\int_{0}^{b}\frac{b}{m}dt\) \(* \int \frac{dx}{1-x^{2}}=tanh^{-1}(x)\)
\(V_{T}tanh^{-1}\left ( \frac{v}{v_{T}} \right )=\frac{b}{m}t\)
\(V(t)=V_{T}tanh\left ( \frac{\frac{b}{m}t}{v_{T}} \right )\)
What is a fictitious force?
Suppose a bus is initially traveling north at constant speed as shown. The bus makes a left turn without changing speed, causing a box on the floor of the bus to slide towards
the right. From the perspective of an observer on the bus, in the same reference frame as the box, there is no force causing the box to move; the box is moving due to an acceleration of the reference frame the box is in.
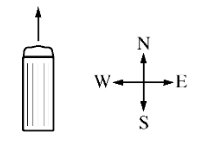
▪ A non–inertial reference frame is one that is accelerating. Newton’s Laws do not apply in non–inertial reference frames.
▪ To solve accelerated reference frame problems: Set the sum of the forces equal to ma, where a is the acceleration of the reference frame itself.
Example A: A pendulum is placed on a cart that is accelerating in the x–direction as shown. The deflection of the bob is 𝜃 = 30°. Find the magnitude and direction of the cart’s acceleration.
Answer/Explanation
Ans: 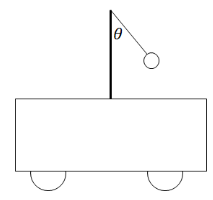
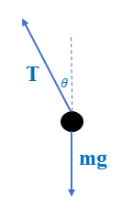
The free–body diagram shows an unbalanced force in the x–direction, even though the bob is not accelerating within its reference frame. To solve for the acceleration, the unbalanced force will be set equal to mass times the acceleration of the non–inertial reference frame. In the vertical direction, the forces simply cancel out:
\(\sum F_{y}=T cos \theta -mg = 0 \rightarrow T = \frac{mg}{cos \theta }\)
In the horizontal direction, the unbalanced force is set equal to ma.
𝐹𝑥 = 𝑇 sin 𝜃 = 𝑚𝑎𝑐𝑎𝑟𝑡
The direction of the acceleration is to the left. The acceleration of the reference frame is the direction of unbalanced force within the frame.
Substituting the tension expression from the vertical direction equation:
\(\rightarrow \frac{mg}{cos\theta }sin\theta =ma_{cart}\rightarrow mg tan \theta =ma_{cart}\)
\(\rightarrow a_{cart}=g tan\theta =\left ( 10\frac{m}{s^{2}} \right )tan 30^{0}\)
\(a_{cart}=5.8 m/s^{2}\)
▪ Note that the tension in the rope in the problem above does not actually cause the deflection of the bob.
There are no net forces inside the cart to cause the deflection. A fictitious force, or an outside apparent force cause balances the horizontal component of the bob.
▪ Fictitious Force – The acceleration of the reference frame itself acts as a force in the system, even though the force does not act on the system.
Example B: A car shaped incline as shown below is accelerating to the left. The coefficient of static friction between the block of mass 𝑚 and the incline is 𝜇. Find the maximum acceleration the car can have before the block begins to slide up the incline.
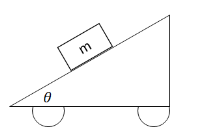
Answer/Explanation
Ans: 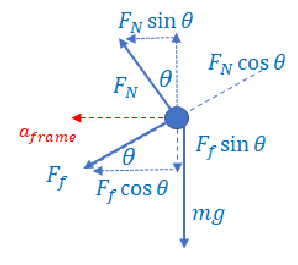
The unbalance force in the free–body diagram is to the left, so each of the forces are broken into their horizontal and vertical components.
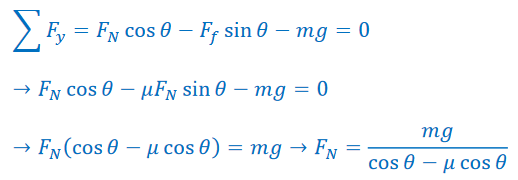
The acceleration is to the left, so the sum of the forces in the x–direction will be set equal to mass times this acceleration. Left will be taken as the positive direction.