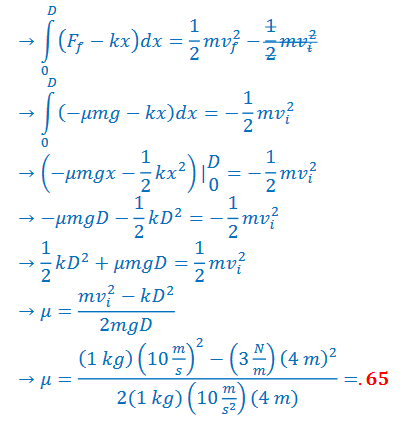What is work?
Work is done when there is a force that acts on a moving system in the direction of the displacement.

*work is a scalar, but can be positive or negative.
*Units of work – Nm, or Joules (J)
▪ Positive Work – A force does positive work if a component of the force acts in the direction of displacement.
▪ Negative Work – A force does negative work if a component of the force acts opposite the direction of displacement.
▪ Zero Work – A force does zero work if the force is perpendicular to displacement, so that no component of force is in direction of displacement.
*If several forces act on an object, the total work is the algebraic sum of the individual works.
Example A: A mass is pulled up an incline that is a distance 𝑑 long by a force F that acts parallel to the plane. The coefficient of sliding friction between the mass and the incline is 𝜇.
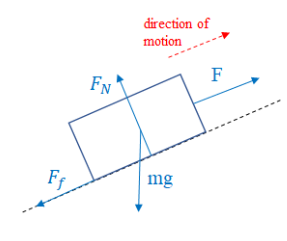
a) What is the work done by the pull force F?
Answer/Explanation
Ans: F does positive work since it points in the direction of motion:
𝑊 = 𝐹𝑑 cos 0 = +𝑭𝒅
b) What is the work done by gravity?
Answer/Explanation
Ans: Gravity does negative work since a component of it (mgsin𝜃) opposes the direction of motion.
𝑊 = (𝑚𝑔 sin 𝜃)𝑑 cos 180° → −𝒎𝒈 𝐬𝐢𝐧 𝜽 𝒅
c) What is the work done the normal force?
Answer/Explanation
Ans: The normal force does zero work since it is perpendicular to the direction of motion.
d) What is the work done by friction?
Answer/Explanation
Ans: Friction does negative work since is opposite the direction of motion.
𝑊 = 𝐹𝑓𝑑 cos 180° = −𝝁𝒎𝒈 𝐜𝐨𝐬 𝜽𝒅
e) What is the total work done on the mass?
Answer/Explanation
Ans: 𝑾 = 𝑭𝒅 − 𝒎𝒈 𝐬𝐢𝐧 𝜽 𝒅 − 𝝁𝒎𝒈 𝐜𝐨𝐬 𝜽𝒅
Calculate work done by a varying force.
▪ If the force applied varies with distance: \(W = \int_{a}^{b}F(x)dx\)
▪ If the force applied varies in direction and magnitude: \(W = \int_{a}^{b}F(x)cos \theta dx\)
Example B: A force varies with distance as given below:
𝐹(𝑥) = 6𝑥2 + 5 sin 𝑥.
Answer/Explanation
Ans: The force is applied to a 3.0 kg object that is initially at rest with no other forces acting. Find the speed of the object after it has been pushed 5 meters.
\(W = \int_{2}^{5}F(-4x^{3})dx=-609 Nm\)
Work to stretch a spring
▪ Review: Hooke’s Law (Force to stretch a spring):
Hooke’s Law relates what distance from equilibrium (x) a spring will be displaced when a force F is applied to stretch or compress the spring.
𝑭 = −𝒌𝒙 
k – spring constant (units: N/m) *the negative sign indicates the force is opposite displacement
▪ Work to stretch a spring: 𝑾 = ∫ 𝑭 𝒅𝒙
Example B: A grocery market uses a non–ideal spring with a force given by \(F = -\frac{1}{2}kx^{3}9.0 kg\) of bananas stretch the spring scale 0.3 m.
What is the spring constant of the scale?
Answer/Explanation
Ans: The spring force counter-acts the weight of the bananas:
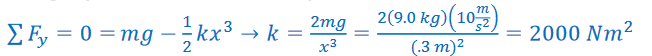
*it is against societal norms to buy so many bananas
How much would work would it take to stretch the spring .5 m?
\(W = \int_{0}^{.5}(\frac{1}{2}kx^{3})dx=250 j\)
What is the work energy theorem?
Objective: Apply the work–energy theorem.
▪ Kinetic Energy – A scalar quantity that measures the energy of an object’s motion.
𝑲 = 𝟏/𝟐𝒎𝒗𝟐
▪ The Work Energy Theorem – The (net) work done by an external force on an object is equal to the change in kinetic energy of the object.
Doing work on a system increases (positive work) or decreases (negative work) that the energy the system has. The net work (by nonconservative forces) is equal to the change in kinetic energy for a system in motion.
W=∆𝐾
➢ *Doing work on a system increases the energy of a system. When a system does negative work, it loses energy.
▪ If force varies with position:
𝑊 = ∫ 𝐹𝑑𝑥 = ∆𝐾
Example A: A 1.0 kg block is attached to a spring (k=3.0 N/m) and rests on a rough horizontal surface. The spring is initially uncompressed. The block is given an initial velocity of 10 m/s and compresses a maximum distance of 4.0 m. What is the coefficient of sliding friction?
Answer/Explanation
Ans: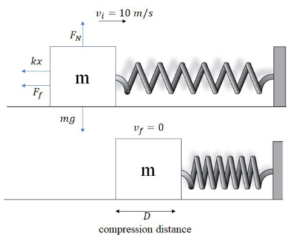
Work done by friction and the spring change the block’s kinetic energy as it compresses the spring.
𝑊 = ∆𝐾