How are displacement, acceleration, and velocity related?
Objective: Apply conservation of energy to solve for unknown quantities.
Total Mechanical Energy: 𝑬 = 𝑼 + 𝑲
Work done by conservative forces
▪ Work done only depends on the starting point and ending point; it is independent of path.
▪ Work done = −(𝑈𝑓 − 𝑈𝑖) = −∆𝑈
▪ Work done is reversible, work on return trip is the negative of work done on the first part. In a closed loop, total work is zero.
▪ If only conservative forces act, no energy is added or removed from the system so the total energy in the system is conserved:
∆𝑬 = ∆𝑼 + ∆𝑲 = 𝟎
𝑼𝒊 + 𝑲𝒊 = 𝑼𝒇 + 𝑲𝒇
Example A: Roller Coaster – A cart is released from rest at the top of a hill with height ℎ. It travels down a frictionless track and goes through a vertical loop with radius R, as shown.
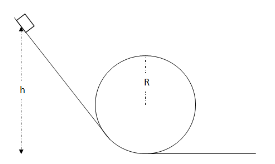
a) Suppose that, at the top of the loop, the track exerts a normal force equal to three times the cart’s weight. Determine an expression for h in this case.
Answer/Explanation
Ans: 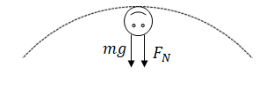
At the top of the loop, both gravity, and normal force on the cart point towards the center of the circle. From the given condition, FN=3mg
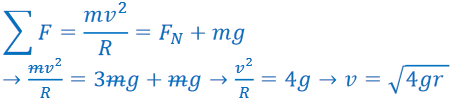
With the speed at the top of the loop, conservation of energy can be used. The height of the cart at the track’s vertical loop is 2R:
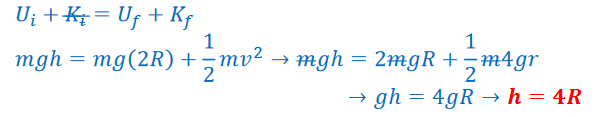
b) If the initial height of the cart were 2R, what angle would a radius drawn to the cart from the center of the loop make with the vertical when the cart falls off the track?
Answer/Explanation
Ans: 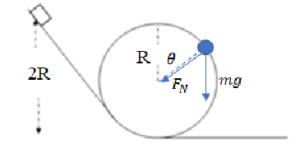
The cart will lose contact with the track at the moment the normal force becomes zero. At the point shown, the weight of the cart does act to keep it a circle, but only the 𝑚𝑔 cos 𝜃 component of weight is a centripetal force.
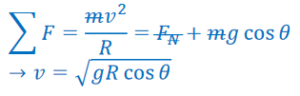
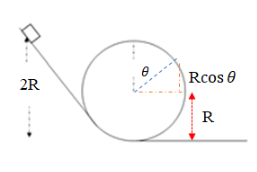
The height of the cart when it makes an angle 𝜃 with the vertical is 𝑅 + 𝑅 sin 𝜃:
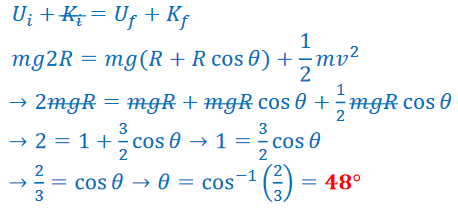
Example B: Spring – A spring toy has a spring constant of k. A ball is placed on top of the spring and the spring is compressed a distance x. Find the maximum height obtained by the ball.
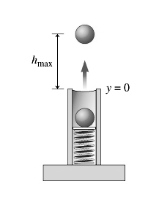
Answer/Explanation
Ans: Elastic potential energy is converted into gravitational potential energy. There is a conversion of kinetic energy in between, but this does not need to be accounted for since there is no lost energy, so any kinetic energy gain will be converted to gravitational potential energy.
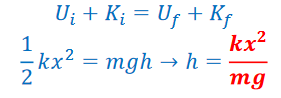
Example C: Pendulum – A 2.0 kg mass is attached to a 1.0 m long string and released from rest at an angle of 60o with the vertical.
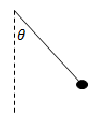
a) Find the speed of the mass at the bottom of the swing.
Answer/Explanation
Ans: 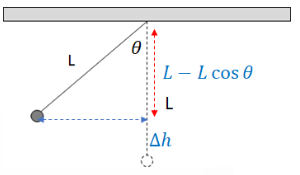
The change in height of a pendulum as it swings down is 𝐿(1 − cos 𝜃). At the bottom of the swing, the pendulum is in circular motion.
vi + ki = vf + kf
\(mg\Delta h=\frac{1}{2}mv^{2}\)
\(\Rightarrow gL(1-cos\theta )=\frac{1}{2}v^{2}\Rightarrow v=\sqrt{2gL(1-cos\theta )}\)
\(\Rightarrow v=\sqrt{2(10\frac{m}{s^{2}})(1m)(1-cos60^{0})}=3.2 m/s\)
b) Find the tension of the mass at the bottom of the swing.
Answer/Explanation
Ans: FBD at bottom
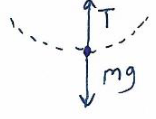
\(\sum F = \frac{mv^{2}}{L}=T-mg\Rightarrow T=\frac{mv^{2}}{L}+mg\)
\(\Rightarrow T = \frac{(2 kg)(3.2 m/s)^{2}}{L}+(2 kg)(10 m/s^{2})=40.5 N\)
Work done by non–conservative forces
▪ Energy lost to dissipative forces is never recovered. In this case, energy with respect to the system is not conserved (though energy is always conserved with respect to the universe).
▪ When non–conservative forces due work, the equation for conservation of energy can be extended to show work entering/leaving the system.
𝑼𝒊 + 𝑲𝒊+𝑾𝑵𝑪 = 𝑼𝒇 + 𝑲𝒇
*𝑊𝑁𝐶: Work done by non–conservative forces
Another way of stating this equation is that the total change in energy in the system is equal to the work done by non–conservative forces.
∆𝑬 = 𝑾𝑵𝑪 = ∆𝑲 + ∆𝑼
Positive work done by nonconservative forces will cause a system to gain mechanical energy. Negative work done by conservative forces will result a loss in mechanical energy.
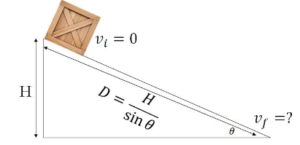
Example D: Incline with Friction – A crate is released from rest at the top of a rough incline of height H and angle 𝜃. Find the speed of the crate at the bottom of the incline.
Answer/Explanation
Ans: As the block slides down the incline, gravitation potential energy is either converted to kinetic energy or lost due to work required to overcome friction.
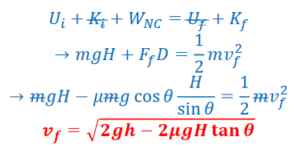
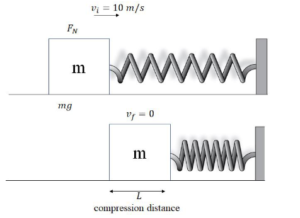
Example E: Spring with Friction – A 1.0 kg block attached to a spring (k=3.0 N/m) and resting on a rough horizontal surface is given an initial velocity of 10 m/s. The maximum compression of the spring is L = 4.0 m. What is the coefficient of sliding friction?
Answer/Explanation
Ans: This is identical to a problem from 3.1, but will be solved with conservation of energy rather than work energy theorem.
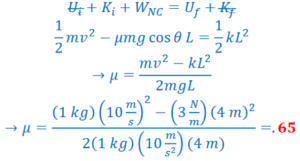
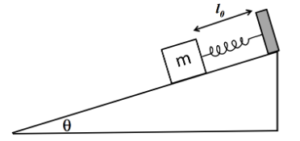
Example F: Spring on incline (with friction) : Oh wow, what a mess. A spring is hanging an incline of angle 𝜃 = 30° as shown. It is displaced a length of 𝑙0 from equilibrium when allowed to stretch down the incline. The block has mass M = 0.5 kg and the spring has a spring constant of k=50 N/m. The coefficient of friction on the inline is 𝜇 = 0.20. Calculate 𝑙0.
Answer/Explanation
Ans: As the block slides down the incline, gravitational potential energy is converted to elastic potential energy of the stretched spring, while some is lost to friction. As the spring slides down the incline, it slides a distance of 𝑙0, while falling a height of 𝑙0 sin 𝜃.
Ui + ki + WNC = Uf + kf
\(mgl_{0}sin\theta -\mu mgcos\theta l_{0}=\frac{1}{2}kl^{0}\)
\(\Rightarrow (.5 Kg)(10 m/s^{2})sin30^{0}l_{0}-(.2)(.5 Kg)(10 m/s^{2})cos30^{0}l_{0}=\frac{1}{2}(50\frac{N}{m})l_{0}^{2}\)
\(\Rightarrow 2.5l_{0}-2.17l_{0}=25{l_{0}}^{2}\)
⇒ l0 = .013 m