How are displacement, acceleration, and velocity related?
▪ Momentum – Measure of how hard it is to stop an object in motion:
\(\vec{p}=m\vec{v}\)
*units of momentum: \(kg\cdot \frac{m}{s}\) (momentum has no special units)
*Momentum is a vector quantity with the direction of momentum being the same as the direction of the velocity of an object.
▪ Impulse – A force applied to a system over time:
𝑱 = 𝑭𝒕 (Physics 1 version)
𝑱 = ∫ 𝑭(𝒕)𝒅𝒕
*Impulse and momentum are both vector quantities.
▪ The Impulse–Momentum Theorem:
An impulse causes a change in momentum
𝑱 = ∆𝒑
Force is the rate at which momentum is changing:
Since impulse is the integral of force, force is defined as the derivative, or rate of change, of momentum:
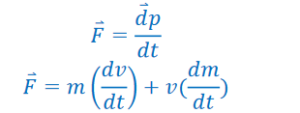
*F=ma is a special case of the above equation for when mass is constant in a system.
Apply the impulse momentum theorem.
Example A: A .10 kg tennis ball hits a racket with a speed of 10 m/s. It rebound in the opposite direction with a speed of 10 m/s. The ball is in contact with the wall for 0.005 s. Find the average force exerted by the racket on the ball.
Answer/Explanation
Ans: 
This problem is solved by using the impulse–momentum theorem.
𝐽 = ∆𝑝 → 𝐹𝑡 = 𝑚𝑣𝑓 − 𝑚𝑣i
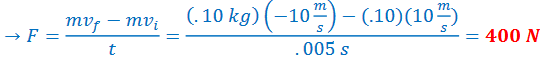
Example B: Continous changing mass momentum problem – Gravel falls vertically on a conveyer belt at a rate of 𝜎 𝑘𝑔/𝑠 as shown.
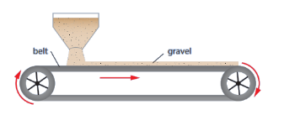
a) Determine:
i. the force that must be applied on the belt to keep it moving at constant speed v.
ii. the power that must be supplied by the motor turning the belt.
iii the rate at which the kinetic energy of the gravel is changing.
Answer/Explanation
Ans: i. Force is the rate of change of momentum; and not just the momentum, but the mowomentum and mochildretum too.
![]()
ii. Since velocity is constant, the equation 𝑃 = 𝐹𝑣 can be used.
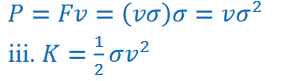
b) Explain why the answers to a) ii and a iii are different.
Answer/Explanation
Ans: Power is the rate at which energy is changing. However, the rate of gain in kinetic energy is less than the power.
The energy that is not converted into kinetic energy is the energy lost in the inelastic collision between the sand and the belt.
I don’t like sand. It’s coarse and rough and irritating and it gets everywhere. Not like AP Physics. In AP Physics everything is soft and smooth.
Apply conservation of momentum.
▪ By impulse–momentum theorem, an outside force acting for a time changes the momentum of a system.
▪ In an isolated system (one in which no external forces act) there is no change in momentum:
\(\vec{p_{i}}=\vec{p_{f}}\)
The velocity of the center of mass is constant.
![]()
Momentum can change if there an impulse. Conservation of momentum applies when there is no outside force on a system.
*Systems may have internal forces that can change the momenta of certain objects in the system, but they have no effect on the momentum of the system as a whole.
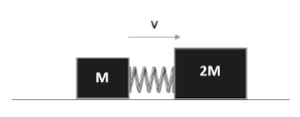
Example C: Two masses travel together to the right as shown. The center of mass of the blocks–spring system has speed v. The massless spring is fixed to the bigger block. The spring compresses and the spring force causes the smaller block to travel left with velocity v to the left. Find the new velocity of the large block after the spring decompresses.
Answer/Explanation
Ans: Conservation of Momentum: 𝑝𝑖 = 𝑝𝑓 *right is defined as the positive direction
Example D: A spaceship ejects full over time as shown. The fuel is ejected at a speed of 𝑣𝑒. As fuel leaves the ship, the ship loses part of its mass, 𝑑𝑚. It also gains a certain velocity, 𝑑𝑣.

a) Determine an expression for the velocity of the rocket over time.
Answer/Explanation
Ans: A spaceship through space and ejects fuel over time as shown. The fuel is ejected at a speed of ve. As fuel leaves the ship, the ship loses part of its mass, dm. It also gains a certain velocity, dv.
Initially, the ship of mass m, and fuel, of mass dm, have a velocity together of v. As the fuel is ejected, the ship has its mass, m without fuel, which has a velocity that has increases by dv. After the ejection, the fuel, of mass dm, travels to with a speed of v (the initial ship’s speed when the fuel was ejected) minus the velocity of the exhaust. All this information can be used to set up a conservation of momentum equation:
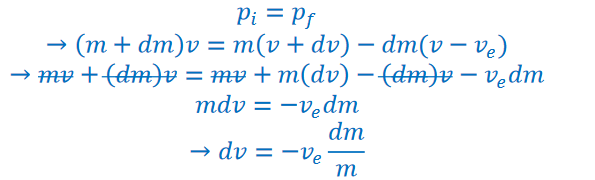
The velocity of the rocket starts at some initial value, 𝑣𝑜 and the mass starts at some value 𝑀0.
b) Determine an expression for the thrust of the rocket (the force propelling the rocket).
Answer/Explanation
Ans: Thrust is the force exerted by the ejected material. If ejection velocity is constant, this force is given by:
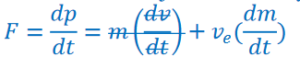
Therefore the general thrust equation is: \(F = v_{e}\frac{dm}{dt}\)