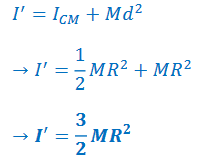How are displacement, acceleration, and velocity related?
Angular Displacement
–Angular displacement of a point that rotates about an axis (that is perpendicular to the plane of the page) is an angle measured in radians.
Units of angular displacement: radians
*𝝅 𝒓𝒂𝒅 = 𝟏𝟖𝟎°
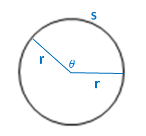
–Relationship between angular displacement and linear distance traveled – For an angle given in radians, the linear distance is equal to the arc length:
𝒔 = 𝒓𝜽
Angular Velocity
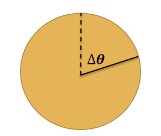
▪ Suppose an object rotates from 𝜃1 at 𝑡1 to 𝜃2 at 𝑡2:
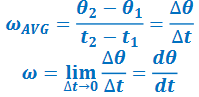
*Since the object is rigid, any point on the object will rotate at the same rate. However, they will not all have the same linear speed.
▪ Relationship between angular velocity and linear velocity –
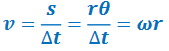
Angular Acceleration
▪ If angular velocity changes, an angular acceleration exists:
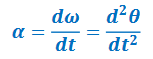
*Relationship between linear and angular displacement: 𝒂 = 𝒓𝜶
Example A: For a spinning object, 𝛼(𝑡) = −4𝑡. If 𝜔(0) = 8 𝑟𝑎𝑑/𝑠 and 𝜃(0) = 10𝜋 𝑟𝑎𝑑, find angular velocity and position as functions of time.
Answer/Explanation
Ans: 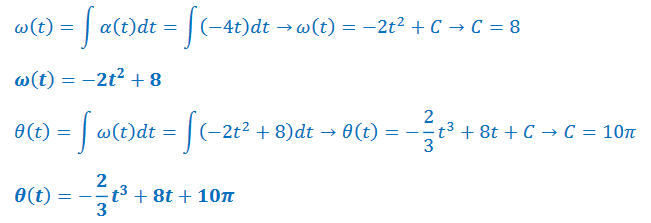
Example B: The wheel in the sky keeps on turning. I don’t know where I’ll be tomorrow. The wheel starts from rest and accelerates at a rate of 1.5 rad/s2. The wheel has a radius of 0.9 m and makes three complete turns.
a) Find the angular velocity of the wheel once it has completed three turns.
Answer/Explanation
Ans: wi = O (starts from rest)
∝ = 1.5 rad/s2
Δθ = 3 rev = 6π rad
wf = ?
wf2 = wf2 + 2 ∝ Δ θ ⇒ \(w_{f}=\sqrt{2\oe \Delta \theta }\)
\(\Rightarrow w_{f}=\sqrt{2(1.5 rad/s^{2})(6\pi rad)}=7.5 rad/s\)
b) Find the linear speed of a point on the edge of the wheel.
Answer/Explanation
Ans: \(v = rw = (.9m)(7.5 rad/s)=6.8 m/s\)
c) Find the linear speed of a point halfway to the wheel’s edge.
Answer/Explanation
Ans: \(v = \left ( \frac{.9m}{2} \right )(7.5 rad/s) = 3.4 m/s\)
The point halfway to the wheel’s edge travels less distance in one rotation, so its linear speed is slower. Both points have the same rotational speed though, as they both go through 2𝜋 in the same unit of time.
d) Find the tangential acceleration and radial acceleration of a point on the edge of the wheel.

Answer/Explanation
Ans: Tangential acceleration: a = r∝ = (.9m) (1.5 rad/s2) = 1.35 m/s2
radial acceleration: \(a = \frac{v^{2}}{r}=\frac{(6.8 m/s)^{2}}{.9m}=51 m/s^{2}\)
How are displacement, acceleration, and velocity related?
Physics 1 Review
▪ In linear motion, inertia is the ability of an object to resist changes in motion as a result of force. Inertia is based only on mass.
▪ In rotational motion, both mass and shape determine resistance to rotation due to force. In general, more mass further from the axis of rotation leads to more resistance to rotation.
Ex: A hollow sphere will resist rotation more than a solid sphere is both have the same mass.
▪ For a point mass 𝐼 = 𝑟2𝑚.
Example A: An Olympic ice skater is spinning and pulls her arms in to speed up her spin. Explain how this is possible with physics.
Answer/Explanation
Ans: It’s harder to make a given mass rotate around an axis that it’s far from than one that it’s close to. When the skater pulls her arms in, she brings more of her mass closer to the center of axis of rotation, thus increasing her angular acceleration.
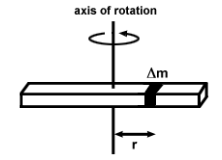
Calculate moment of inertia when an object is pivoted at its center of mass.
To calculate moment of inertia, divide the object into small particles, each of mass ∆𝑚 at a distance 𝑟 from the axis of rotation.
𝐼 = ∫ 𝑟2 𝑑𝑚
*For point mass*
𝐼 = 𝑚𝑟2
*Units of moment of inertia: 𝑘𝑔 𝑚2
Example B: Moment of Inertia for a rod with an axis perpendicular to the rod. ![]()
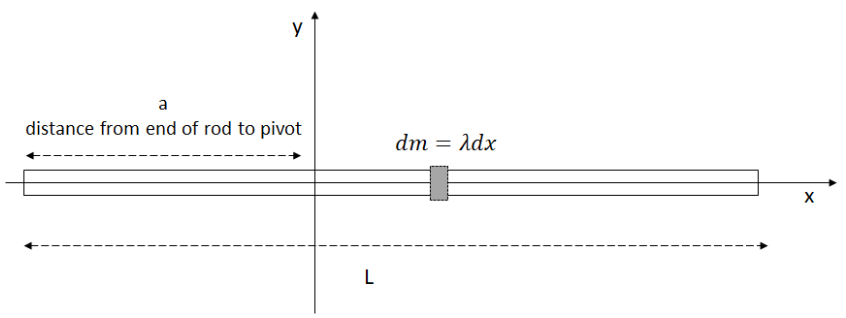
Answer/Explanation
Ans: 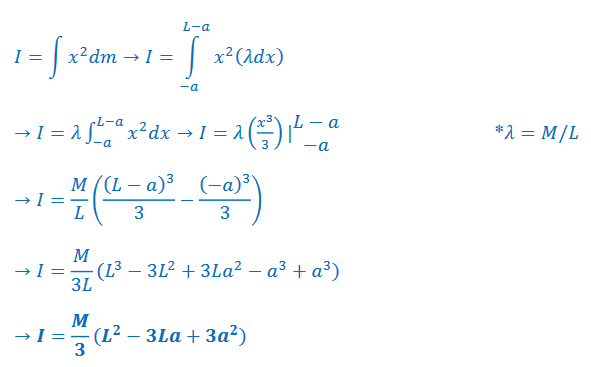
*If rod is pivoted at end (a=0):
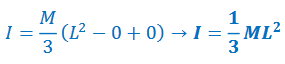
*If rod is pivoted at center: (a=L/2)
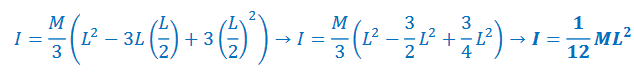
Example C: Cylinder about an axis through its center.
Answer/Explanation
Ans: 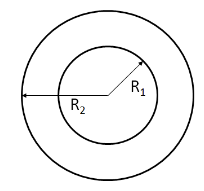
𝐼 = ∫ 𝑟2𝑑𝑚
*dm=𝜌𝑑𝑉 𝜌 = 𝑣𝑜𝑙𝑢𝑚𝑒 𝑚𝑎𝑠𝑠 𝑑𝑒𝑛𝑠𝑖𝑡𝑦
dV=d(𝜋𝑟2𝐿) = 2𝜋𝑟𝐿𝑑𝑟 L = length of cylinder (needs to cancel
eventually, does not affect I)
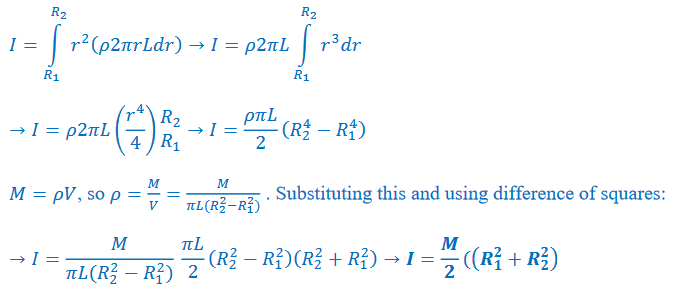
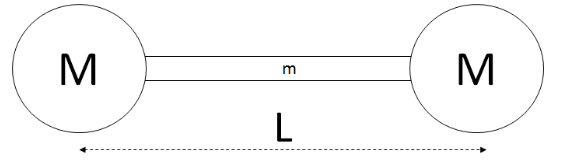
Example D: Moment of inertia of “point masses” on another object about the center:
Answer/Explanation
Ans: This system consists of 3 objects:
A rod of length L and mass m pivoted about its center: \(I=\frac{1}{12}mL^{2}\)
2 spheres at a distance of L/2 from the center of rotation. Both can be treated as a point masses:
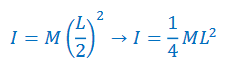
The total moment of inertia is the sum of the three individual moments of inertia:
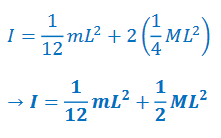
Apply the parallel–axis theorem.
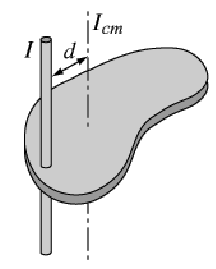
If an object is not pivoted at its center of mass, the moment of inertia can be found using the moment of inertia about the object’s center of mass: 𝑰𝒑 = 𝑰𝒄𝒎 + 𝒎𝒅𝟐
Ip : Moment of inertia about an axis parallel to central axis.
Icm: Moment of inertia about center of mass.
m: mass
d: distance between axes
*Ip is always greater than Icm*
Example E: Consider a solid cylinder of radius R and mass M. Find the moment of inertia of a solid cylinder of radius R and mass M about:
a) Its center
Answer/Explanation
Ans: The result of example C for a cylindrical shell: \(I=\frac{M}{2}(R_{1}^{2}+R_{2}^{2})\)
For a solid cylinder, the inner radius is zero: R1=0:
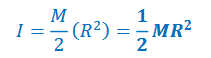
b) An axis tangents to the cylinder at its outer edge.
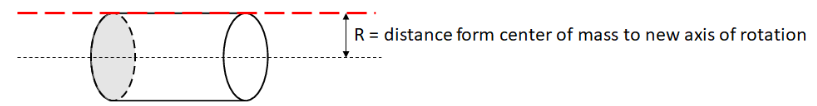
Answer/Explanation
Ans: