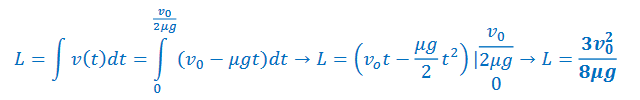What determines the total energy of a moving object?
A rotating object has kinetic energy because all the particles that make up the object are in motion. The total kinetic energy of a rotating object is the sum of the kinetic energy of all the particles.
Solve for rotational kinetic energy.
Kinetic Energy for Rotation: – Energy an object possess due to its rotational motion.
\(K=\frac{1}{2}I\omega ^{2}\)
Example A: A block of mass m is attached to a string that goes over a cylindrical pulley of mass M and radius R. When the block is released, the pulley begins to turn as the
block falls. Calculate the acceleration of the block.

Answer/Explanation
Ans: This system involves both linear and rotational motion, so both F=ma and 𝜏 = 𝐼𝛼 are both to be used for the mass and pulley respectively. The direction of motion will be
take as the positive direction for both.
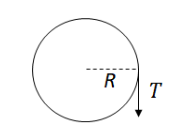
Pulley: Clockwise is the direction of motion:
∑ 𝜏 = 𝐼𝛼
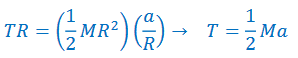
Block: Down is the positive direction:
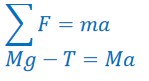
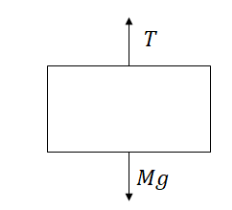
Combing the equations using substitution
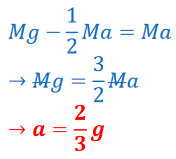
Apply the work–energy theorem
▪ A force applied to a rotating body does work on the body. The work can be expressed with torque and angular displacement:
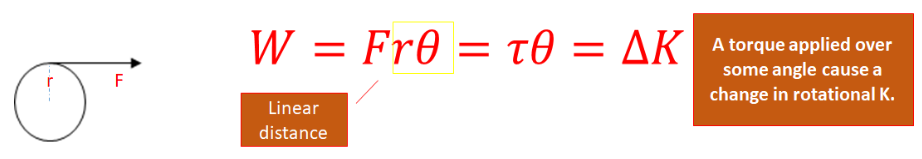
*only the component of the force perpendicular to the axis of rotation does work.
▪ Power: \(P=\frac{dW}{dt}\)
Analyze the motion of a rolling object.
▪ Total kinetic energy of a rigid body – A rolling object has both linear kinetic and rotational kinetic energy.


Example B: The wheel on the ground keeps on turning. Show that the radius of the wheel does not affect its total kinetic energy.
Answer/Explanation
Ans: 
*this assumes that the wheel rolls without slipping*
▪ Rotating – Each point on wheel has a different linear velocity.
▪ Sliding – Each point on wheel has the same linear velocity.
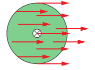
▪ Rolling without slipping – the point of contact between the wheel and surface has no linear velocity.
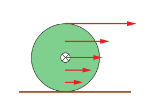
*When friction is present and an object rolls without slipping, friction is used to convert rotational kinetic energy into linear kinetic energy. The magnitude of the negative rotational work done by friction equals the positive linear work done by friction. Thus friction does no net–work on the wheel. *
Example C: A solid wheel of mass M and radius R moves up an incline as shown. The speed of the ring is 𝑣 as it enters the incline.
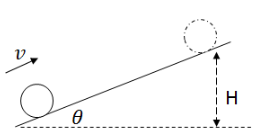
*Background* When friction is present, it is used to convert rotational kinetic energy into linear kinetic energy. The magnitude of the negative rotational work done by friction equals the positive linear work done by friction. Thus friction does no net–work.
a) Find how high up the incline the wheel goes if: the wheel slips while going up the incline. (frictionless)
Answer/Explanation
Ans: If there is no friction, the rotational motion of the wheel will not be converted to linear motion. This problem works the same as sliding.
Ui + ki = Of + kf
\(\frac{1}{2}Mv^{2}=\mu gH\Rightarrow H =\sqrt{2gH}\)
b) Find how high up the incline the wheel goes there is no slipping of the wheel as it moves up the incline. (friction is present)
Answer/Explanation
Ans: If there is friction, the rotational of the wheel helps it move forward and it can convert its rotational kinetic energy into potential energy.
Ui + ki = Uf + kf
\(\frac{1}{2}Mv^{2}+\frac{1}{2}I\omega ^{2}=MgH\)
\(\frac{1}{2}Mv^{2}+\frac{1}{2}\left ( \frac{1}{2}MR^{2} \right )\left ( \frac{V}{R} \right )^{2}=MgH\)
\(\frac{1}{2}v^{2}+\frac{1}{4}v^{2}=gH\)
\(\frac{3}{4}v^{2}=gH \Rightarrow h = \frac{3v^{2}}{4g}\)
In a), only the linear kinetic energy is converted to potential energy. In b), both linear and rotational kinetic energy are converted into gravitational potential energy, which is why the answer to b) is greater.
c) How would the answer to b) change if the wheel were solid?
Answer/Explanation
Ans: In this case, there would be more initial energy (more I at the beginning), so the wheel will go higher.
Example D; Rolling down an incline: A wheel of radius M and radius R rolls without slipping down an incline.
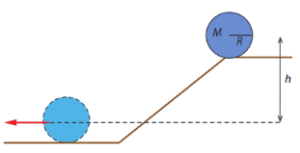
a) Find the linear speed of the center of mass of the wheel when it reaches the bottom of the incline.
Answer/Explanation
Ans: Using conservation of energy:
Ui + ki = Uf + kf
\(MgH = \frac{1}{2}Mv^{2}+\frac{1}{2}\left ( \frac{1}{2} MR^{2}\right )\left ( \frac{V}{R} \right )^{2}\)
\(MgH = \frac{1}{2}Mv^{2}+\frac{1}{4}Mv^{2}\)
\(gH = \frac{3}{4}v^{2}+\Rightarrow v = \sqrt{\frac{4gH}{3}}\)
b) Calculate the acceleration of the wheel down the incline.
Answer/Explanation
Ans: The force of friction applies a positive torque since it causes the wheel to rotate downhill, but a negative force since it resists the sliding motion downhill. *friction always is to be taken as acting uphill on an incline. Gravity (the parallel component) is a positive force since it propels the wheel downhill. Gravity causes no torque since it acts at the center of mass. The normal force applies no torque or force since it is parallel to the axis of rotation (no torque) and has no component in the direction of motion (no force).
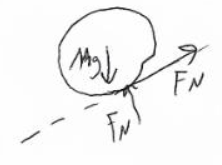
\(\sum F_{“}=Ma = Mgsin\theta -F_{f}\) ∑τ = I ∝
\(Ma = Mgsin\theta -\frac{1}{2}Ma\) \(F_{f}R=\frac{1}{2}MR^{2}(\frac{a}{R})^{2}\)
\(a= \frac{2}{3}gsin\theta \) \(F_{f}=\frac{1}{2}Ma\)
c) To prevent slipping, there are two conditions: 𝑣 = 𝑟𝜔 and 𝜇 = 𝑚𝑔𝑐𝑜𝑠𝜃.
Answer/Explanation
Ans: \(F_{f}=\mu Mgcos\theta =\frac{1}{2}Ma\)
\(\mu Mgcos\theta =\frac{1}{2}M\frac{2}{3}gsin\theta \)
\(\mu =\frac{1}{3}tan\theta \)
Example E: Rolling with slipping – A ring of mass M, radius R, and rotational inertia MR2 is initially sliding on a frictionless surface at constant velocity v0 to the right, as shown. At time t = 0 it encounters a surface with coefficient of friction 𝜇 and begins sliding and rotating. After traveling a distance L, the ring begins rolling without sliding.
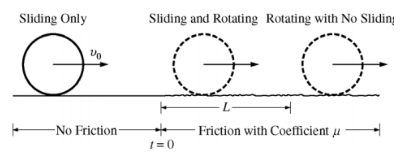
a) Derive an expression for the magnitude of the following as the ring is sliding and rotating.
i. The linear velocity of the ring as a function of time t
Answer/Explanation
Ans: Friction acts a resistive force to slow down the linear motion:
𝑀𝑎 = 𝐹𝑓 → 𝑀𝑎 = −𝜇𝑀𝑎 → 𝑎 = −𝜇𝑔
The velocity changes as a function of time based on this negative acceleration after starting at v0.
𝑣(𝑡) = 𝑣𝑖 + 𝑎𝑡 → 𝒗(𝒕) = 𝒗𝟎 − 𝝁𝒈𝒕
ii. The angular velocity of the ring as a function of time t
Answer/Explanation
Ans: Friction acts as a positive rotational force since it makes the object rotate:
𝐼𝛼 = 𝐹𝑓𝑅 → (𝑀𝑅2)𝛼 = 𝜇𝑀𝑔𝑅 → 𝛼 = \(\frac{\mu g}{R}\)
\(\omega (t)=\omega _{t}+\alpha t\rightarrow \omega (t)=\frac{\mu g}{R}t\)
b) Derive an expression for the time it takes the ring to travel the distance L
Answer/Explanation
Ans: The wheel will start rolling without slipping when 𝑣(𝑡) = 𝜔(𝑡)𝑅
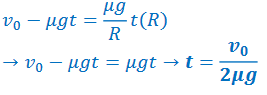
c) Derive an expression for the magnitude of the velocity of the ring immediately after it has traveled L.
Answer/Explanation
Ans: 
d) Derive an expression for the distance L.
Answer/Explanation
Ans: