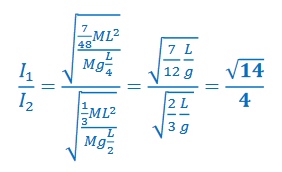What is the equation for simple harmonic motion?
Simple Harmonic Motion
▪ In period motion, an object moves repeatedly over the same path in equal intervals for time. The repetitive movements are called oscillations. If periodic motion is directed towards an equilibrium position, the motion is simple harmonic motion.
▪ If an object undergoing periodic motion is in simple harmonic motion, it has two simple characteristics:
–The force acting on the object is directed towards the equilibrium position.
–The force is proportional to the distance from equilibrium.
A mass vibrating at the end of a spring undergoes simple harmonic motion
▪ The restoring force for a mass–spring system is the force that causes the system to return to equilibrium is given by Hooke’s Law:
Hooke’s Law: The restoring force of a spring varies linearly with the displacement from equilibrium and acts in the opposite direction –
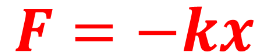
Simple Harmonic Motion Equation
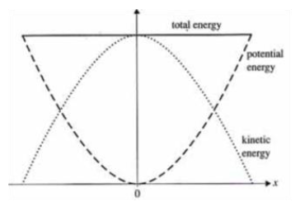
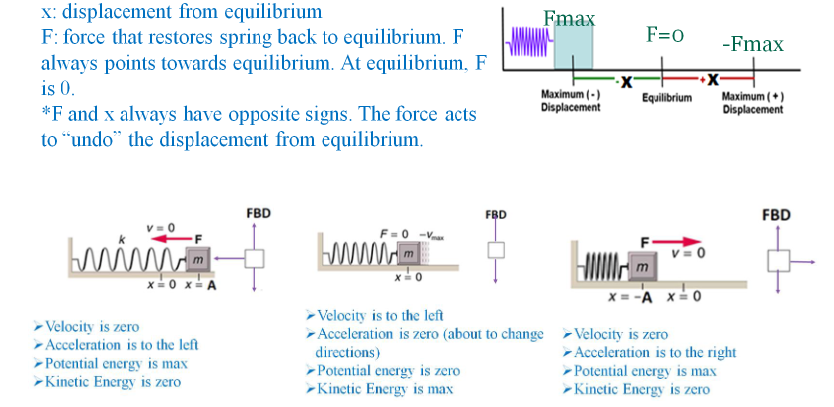
In simple harmonic motion, acceleration is not constant. Kinematics from unit 1 can’t be used. However, conservation of energy applies.
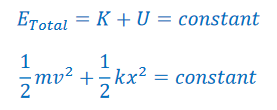
At max displacement (the amplitude), x = A and v = 0. At equilibrium, x =0 and v is at its maximum value:
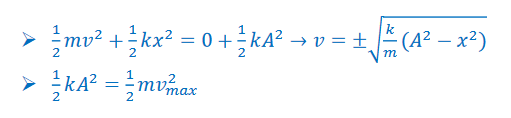
*Background Info* General Equation for Simple Harmonic Motion
The differential equation for a simple harmonic oscillator is given by: \(\frac{d^{2}x}{dt^{2}}+\omega ^{2}x=0.\) The general solution to this differential equation is 𝑥(𝑡) = 𝐴 cos(𝜔𝑡 + 𝜙). The period of the function is 2𝜋 𝜔 . Since the differential equation is a little above Calc 1, the main goal in physics C will be to get the equation in the form of \(\frac{d^{2}x}{dt^{2}}+\omega ^{2}x=0.\) and know how to use this to get the general position function and period.
▪ Simple Harmonic Motion Equation for Springs:
![]()
Comparing this to the general harmonic motion differential equation \(\left ( \frac{d^{2}x}{dt^{2}}+\omega ^{2}x=0 \right ), \omega =\sqrt{\frac{k}{m}},\) so the period can be found to be \(T=\frac{2\pi }{\omega }=\frac{2\pi }{\sqrt{\frac{k}{m}}}\rightarrow T=2\pi \sqrt{\frac{m}{k}}\)
The general solution to the equation is 𝑥(𝑡) = 𝐴 cos(𝜔𝑡 + 𝜙), so for a spring, the general equation is: \(x(t)=A cos (\sqrt{\frac{k}{m}}t + \phi )\)
Velocity and acceleration functions can be found using simple differentiation:

Example A: A 0.2 kg mass vibrates with SHM with amplitude 0.50 m and frequency 5.0 Hz. Find:
a) the total energy of the motion.
Answer/Explanation
Ans: The spring constant, k, can be found using the frequency: 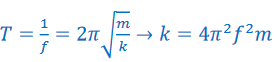
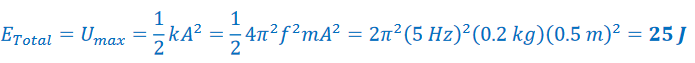
b) the maximum velocity.
Answer/Explanation
Ans: 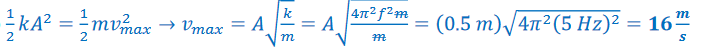
c) The maximum acceleration.
Answer/Explanation
Ans: ![]()
*the negative sign was dropped since it does not affect the magnitude of the maximum acceleration.
d) The time it takes to move from 25 cm to the left of the equilibrium point to 25 cm to the right of the equilibrium point.
Answer/Explanation
Ans: 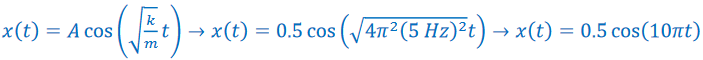
*Phase constant is ignored since we are only looking for a difference in times, t = 0 is defined as when the object is at x = 0.5 m. This question needs to be solved in radians.
𝑡1 : − .25 = 0.5 cos(10𝜋𝑡) → 𝑡1 = ~.068 𝑠
𝑡2: .25 = 0.5 cos(10𝜋𝑡) → 𝑡2 = ~.033 𝑠
∆𝑡 = 𝑡1 − 𝑡2 = ~. 𝟎𝟑𝟓 𝒔
Some equations that can be derived if initial conditions for positive and velocity are given: 𝑥0, 𝑣𝑜
𝑥(𝑡) = 𝐴 cos(ω𝑡 + 𝜙), At t = 0, 𝑥0 = 𝐴𝑐𝑜𝑠(𝜙)
𝑣(𝑡) = −𝐴ω sin(𝜔𝑡 + 𝜙), At t = 0, 𝑣0 = −𝐴𝜔 sin 𝜙
➢ Equations for phase angle, 𝜙:
\(cos\phi =\frac{x_{0}}{A}, \) \(sin =\frac{-v_{0}}{\omega _{A}}, \) \(tan\phi =-\frac{v_{0}}{\omega x_{0}}\)
➢ Equation that relates initial conditions to amplitude:
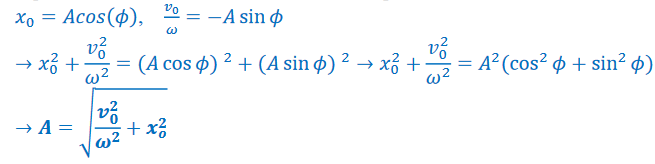
Example B: An object executes SHM with angular frequency of 0.50 Hz. The object is initially 10 cm from its equilibrium position and moving back toward the equilibrium with a velocity of –5.0 cm/s.
a) Find the period of the motion.
Answer/Explanation
Ans: \(T=\frac{2\pi }{\omega }=\frac{2\pi }{.5Hz }\rightarrow T=4\pi s\)
b) Find an expression for the object’s displacement as a function of time.
Answer/Explanation
Ans: Using the equations derived above to find amplitude and phase constant:
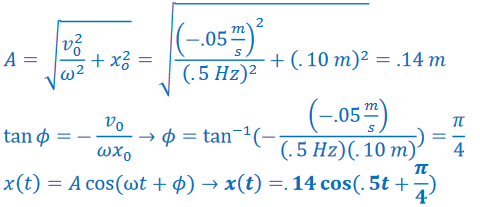
c) Find an expression for the object’s velocity as a function of time.
Answer/Explanation
Ans: 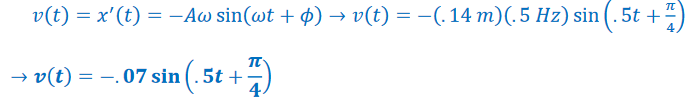
Vertical Springs
Example C: A mass m=1.0 kg is dropped onto a vertical spring whose force constant in k = 2 N/m. The initial speed of the mass is vo =22 m/s after it sticks to the spring. The spring is unstretched at this moment. What is the amplitude of its subsequent motion?
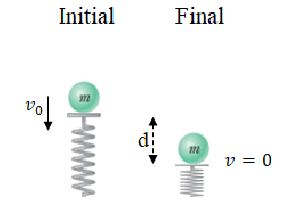
Answer/Explanation
Ans: 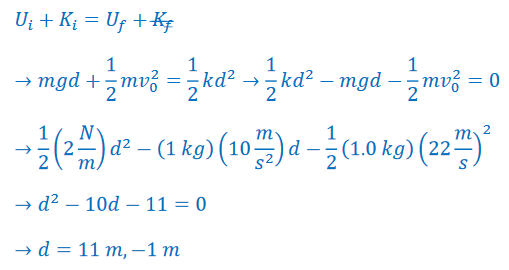
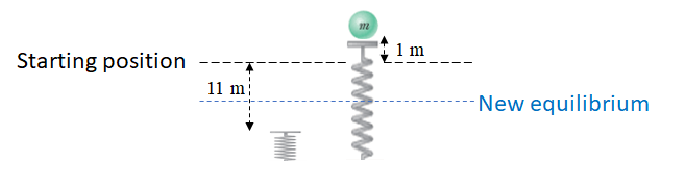
Since d was defined as distance below the starting position, this result means the object will oscillate between going 11 m below and 1 m above the starting position.
The amplitude is then 6 m.
Spring Combinations
▪ Whenever two springs are connected in parallel, the total force of the springs is the sum of the two.

▪ Whenever springs are connected in series, the effective spring constant is smaller than either springs individual constant since each spring stretches a smaller amount for the same total linear displacement of the mass.

Example D: A car with a mass of 900 kg is constructed so that its frame is supported by four springs. Each spring has a force constant of 20,000 N/m. Two people riding in the car have a combined mass of 160 kg. Find the frequency of vibration of the car after it is driven over a pothole in the road.
Answer/Explanation
Ans: The 4 shocks are springs in parallel, so the springs constants add:
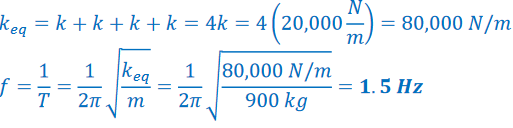
Damping
In reality, the energy of a system will decrease overtime, in a process called damping. The mathematics of damping is explored in differential equations courses.
Example E: Sketch a kinetic, potential, and total energy vs. time graph for a damped mass–spring system.
Answer/Explanation
Ans:
▪ Underdamped system – Resistant force is small; allowing for some oscillations before the system comes to rest eventually.
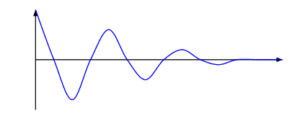
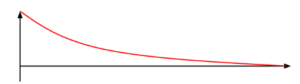
▪ Overdamped system – Systems comes to rest at equilibrium in the quickest time possible without oscillating.
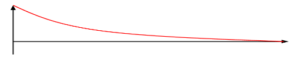
▪ Critically damped system – System comes to rest without oscillating, but after a longer time than it would normally take to return to equilibrium.
How is a pendulum an approximation of Simple Harmonic Motion?
The Simple Pendulum
▪ A simple pendulum is an ideal model consisting of a point mass suspending from a weightless string.
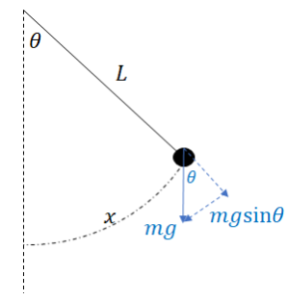
When an ideal pendulum is displaced a small angle 𝜃 from equilibrium (the vertical), the restoring force towards equilibrium is mgsin𝜃.
*For small angles, sin 𝜃 ≈ 𝜃. Since x is an arc of a circle of radius L,
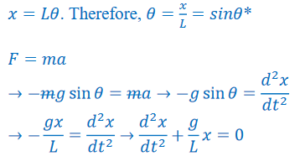
Comparing this to the general harmonic motion differential equation \(\left ( \frac{d^{2}x}{dt^{2}}+\omega ^{2}x=0 \right ),\omega =\sqrt{\frac{g}{L}},\) so the period is \(
Using the general solution, 𝑥(𝑡) = 𝐴 cos(𝜔𝑡 + 𝜙), with the amplitude (max displacement of x) equal to the largest arc length (L𝜃), the general solution for the x–position for an ideal pendulum is:
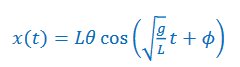
▪ The period of a pendulum is independent of mass. It depends only on length and acceleration due to gravity for small amplitude (15o or less).
▪ A simple pendulum only approximates simple harmonic motion. It differs only slightly from simple harmonic motion for small amplitudes; however, the restoring force, gravity, does not point towards equilibrium.
Example A: A pendulum consists of a 5.00 kg mass suspended from a 2.00 m wire. The pendulum is pulled 10.0 cm from the vertical and released from rest.
*These questions is also easily solved using conservation of energy methods from previous topics. They will be solve with harmonic motion methods here.
a) What is the maximum velocity of the mass?
Answer/Explanation
Ans: 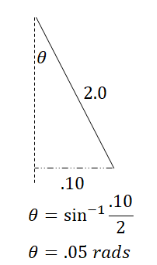
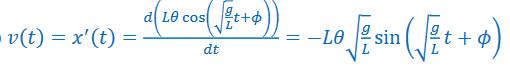
The maximum value of this velocity function has a magnitude of \(L\theta \sqrt{\frac{g}{L}}.\)
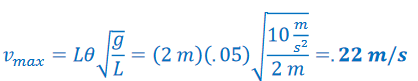
b) What is the acceleration of the mass?
Answer/Explanation
Ans: 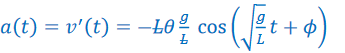
The maximum value of the acceleration function is 𝑔𝜃.
![]()
c) What is the period of the motion?
Answer/Explanation
Ans: ![]()
d) What is the tension in the wire at the bottom of the swing?
Answer/Explanation
Ans: 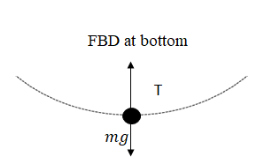
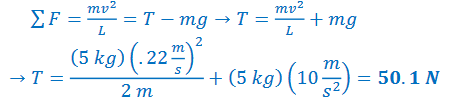
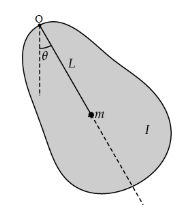
The Physical (real, non–ideal) Pendulum
▪ The object on the right is in equilibrium when the center of mass (m) is below the pivot point (O). When the mass is displaced a certain angle from equilibrium, there is a restoring torque:
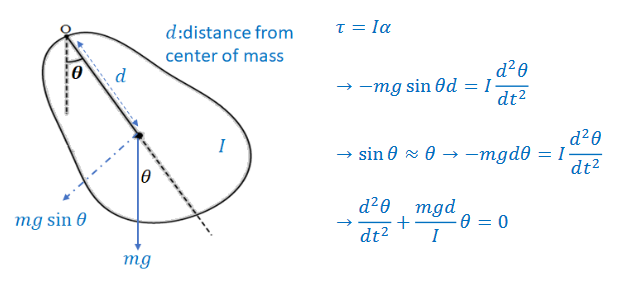
Comparing this to the general harmonic motion differential equation \(\left ( \frac{d^{2}x}{dt^{2}} +\omega ^{2}x=0\right ),\omega =\sqrt{\frac{mgd}{I}},so\)
the formula for a period of a physical pendulum is \(T=\frac{2\pi }{\omega }=\frac{2\pi }{\sqrt{\frac{g}{L}}}\rightarrow T=2\pi \sqrt{\frac{I}{mgd}}\)
General solution for angular position as a function of time: \(\theta (t)=\theta cos(\sqrt{\frac{mgd}{I}}t+\phi) \)
Example B: A thin uniform rod is pivoted at a point one quarter of its length from one end and the period is measured. Then the rod is pivoted at its end and its period is measured again. Find the ratio of the first period to the second period.
Answer/Explanation
Ans: In the equation for the period of a physical pendulum, \(T = 2\pi \sqrt{\frac{I}{mgd}},\) the d is the distance from the pivot to the center of mass.