What is center of mass?
In a system with no external forces, the velocity of the center of mass of a system is constant. This is another way of stating conservation of momentum.
Calculate center of mass.
▪ The center of mass, also called center of gravity, for a collection of particles is the average position of the particles, weighted according to their relative masses.
▪ The center of mass is the “balance point” of an object. For a symmetrical object, the center of mass is at the geometric center.
▪ Calculating center of mass

▪ The velocity of the center of mass is simply the derivative of the center of mass with respect to time:
Example A: Derive an expression for the center of the mass for the shape shown below. Both rectangles have equal mass.
Answer/Explanation
Ans: 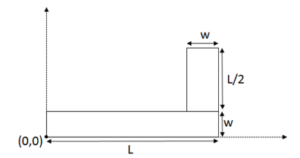
The bottom rectangle has a center of mass at \(\left ( \frac{L}{2},\frac{w}{2} \right ).\)
The top rectangle has center of mass at \(\left ( L-\frac{w}{2},W+\frac{L}{4} \right )\)
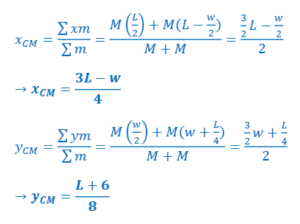
Example B: T–Pain, who has a mass of 80 kg is on a 240 kg boat. He walks 2.0 m/s relative to the boat, starting from the back of the boat and walking toward the front. The boat is 1– m long.
a) What is the velocity of the boat relative to the water?
Answer/Explanation
Ans: 
The center of mass of the person–boat system cannot move relative to the water as there is no outside force (walking across the boat is an internal force). Therefore, if T–Pain walks one way across the boat, the boat must move in the opposite direction so the center of mass of the system doesn’t move. The velocity of the center of mass was zero before T–Pain started walking, so it must stay zero.
Velocity of center of mass formula: \(v_{CM}=\frac{\sum mv}{\sum m}\)
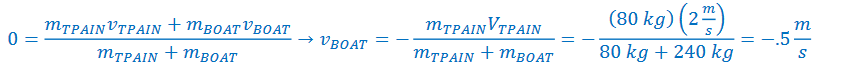
The boat moves 0.5 m/s opposite T–Pain. It moves slower as it has more mass.
b) If T–Pain walks 8.0 m across the deck of the boat and starts on the very left end of the boat, how far does the boat move?
Answer/Explanation
Ans: 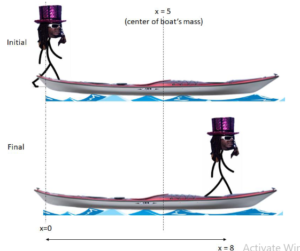

→ 𝑥𝐶𝑀𝑓 = 5.75 𝑚 𝑓𝑟𝑜𝑚 𝑙𝑒𝑓𝑡
Since the center of mass shifts 2 m to the right, the boat must move 2m opposite T–Pain’s direction of motion (left) to keep its center of mass unmoved with respect to the water.
Example C: Find the center of mass of a rod of length L and mass M. ![]()
Answer/Explanation
Ans: The center of mass will only be found in the x–direction since it is assumed to have negligible height. The rod is broken up into infinitely many tiny dm’s, each dm is equal to the linear mass density𝜆) multiple by the infinitely small length, dx. Since the rod is uniform, the linear mass density if \(\lambda =\frac{M}{L}.\)
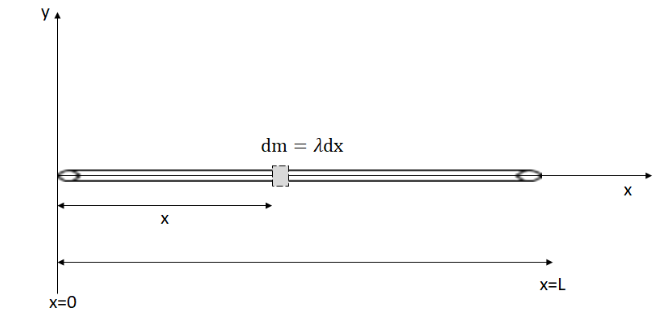
This answer is hopefully not surprising.