Question
1 Find the term independent of $x$ in the expansion of $\left(x-\frac{3}{2 x}\right)^6$. [3]
▶️Answer/Explanation
Ans:
$
\left(x-\frac{3}{2 x}\right)^6
$
Term is ${ }^6 \mathrm{C}_3 \times x^3 \times\left(\frac{-3}{2 x}\right)^3$
$
\rightarrow-67.5 \mathrm{oe}
$
Question
 Answer/Explanation
Answer/Explanation
Ans:
$
\text { (i) } \quad \begin{aligned}
& 2 \sin 2 x=6 \cos 2 x \\
& \tan 2 x=k \\
& \rightarrow \tan 2 x=3 \text { or } k=3
\end{aligned}
$
(ii)
$
\begin{aligned}
x= & \left(\tan ^{-1}(\text { their } k)\right) \div 2 \\
& \left(71.6^{\circ} \text { or }-108.4^{\circ}\right) \div 2 \\
& x=35.8^{\circ},-54.2^{\circ} \\
x= & 0.624^{\mathrm{c}},-0.946^{\mathrm{c}} \\
x= & 0.198 \pi^{\mathrm{c}},-0.301 \pi^{\mathrm{c}}
\end{aligned}
$
Question
3 (i) Find the term independent of $x$ in the expansion of $\left(\frac{2}{x}-3 x\right)^6$.[2]
(ii) Find the value of $a$ for which there is no term independent of $x$ in the expansion of
$
\left(1+a x^2\right)\left(\frac{2}{x}-3 x\right)^6
$
▶️Answer/Explanation
Ans:
3(i) $\quad 6 \mathrm{C} 3\left(\frac{2}{x}\right)^3(-3 x)^3 \mathrm{SOI}$ also allowed if seen in an expansion
-4320 Identified as answer
3(ii) $\quad 6 \mathrm{C} 2\left(\frac{2}{x}\right)^4[(-) 3 x]^2 \quad$ SOI clearly identified as critical term
$15 a \times 16 \times 9-$ their $4320(=0)$
$a=2$
Question
4(i) Prove the identity $(\sin \theta+\cos \theta)(1-\sin \theta \cos \theta) \equiv \sin ^3 \theta+\cos ^3 \theta$. [3]
(ii) Hence solve the equation $(\sin \theta+\cos \theta)(1-\sin \theta \cos \theta)=3 \cos ^3 \theta$ for $0^{\circ} \leqslant \theta \leqslant 360^{\circ}$
▶️Answer/Explanation
Ans:
4(1). $(\sin \theta+\cos \theta)(1-\sin \theta \cos \theta)=\sin \theta+\cos \theta$.
LHS $=\sin \theta+\cos \theta-\sin ^2 \theta \cos \theta-\sin \theta \cos ^2 \theta$
$
=\sin \theta\left(1-\cos ^2 \theta\right)+\cos \theta\left(1-\sin ^2 \theta\right) \text { or }\left(s+c-c\left(1-c^2\right)-\mathrm{s}\left(1-\mathrm{s}^2\right)\right)
$
Uses $\sin ^2 \theta+\cos ^2 \theta=1 \rightarrow \sin ^3 \theta+\cos ^3 \theta$ (RHS)
$\mathrm{Or}$
or
$\begin{aligned} & \text { LHS }=(\sin \theta+\cos \theta)\left(\sin ^2 \theta+\cos ^2 \theta-\sin \theta \cos \theta\right) \\ & =\sin ^3 \theta+\sin \theta \cos ^2 \theta-\sin ^2 \theta \cos \theta+\cos \theta \sin ^2 \theta+\cos ^3 \theta-\sin \theta \cos ^2 \theta=\sin ^3 \theta+\cos ^3 \theta\end{aligned}$
4(ii) $\quad(\sin \theta+\cos \theta)(1-\sin \theta \cos \theta)=3 \cos ^3 \theta \rightarrow \sin ^3 \theta=2 \cos ^3 \theta$
$\rightarrow \tan ^3 \theta=2 \rightarrow \theta=51.6^{\circ}$ or $231.6^{\circ}$ (only)
Question
5 The first three terms of an arithmetic progression are $4, x$ and $y$ respectively. The first three terms of a geometric progression are $x, y$ and 18 respectively. It is given that both $x$ and $y$ are positive.
(i) Find the value of $x$ and the value of $y$. [4]
(ii) Find the fourth term of each progression. [3]
▶️Answer/Explanation
Ans:
5(i) From the AP: $x-4=y-x$
From the GP: $\frac{y}{x}=\frac{18}{y}$
Simultaneous equations: $y^2-9 y-36=0$ or $2 x^2-17 x+8=0$
Question
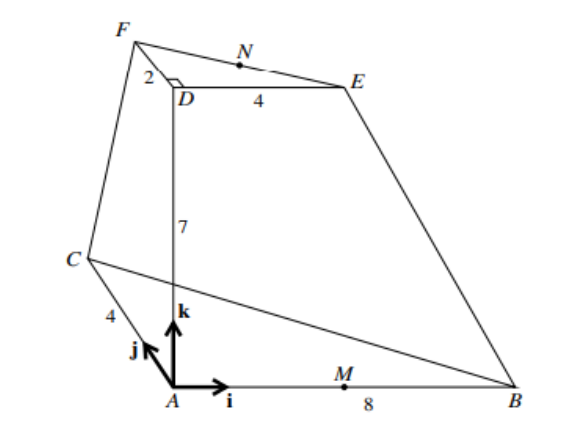
▶️Answer/Explanation
Ans:
6 (i) $\quad \mathbf{M F}=-4 \mathbf{i}+2 \mathbf{j}+7 \mathbf{k}$
6(ii) $\quad \mathbf{F N}=2 \mathbf{i}-\mathbf{j}$
6(iii) $\quad \mathbf{M N}=-2 \mathbf{i}+\mathbf{j}+7 \mathbf{k}$
(iv) MF.MN $=8+2+49=59$
$|\mathbf{M F}| \times|\mathbf{M N}|=\sqrt{4^2+2^2+7^2} \times \sqrt{2^2+1^2+7^2}$
$\cos F M N=\frac{+/-59}{\sqrt{69} \times \sqrt{54}}$
$F M N=14.9^{\circ}$ or 0.259
Question
7 (a) Prove the identity $\frac{1+\sin \theta}{\cos \theta}+\frac{\cos \theta}{1+\sin \theta} \equiv \frac{2}{\cos \theta}$. [3]
(b) Hence solve the equation $\frac{1+\sin \theta}{\cos \theta}+\frac{\cos \theta}{1+\sin \theta}=\frac{3}{\sin \theta}$, for $0 \leqslant \theta \leqslant 2 \pi$. [3]
▶️Answer/Explanation
Ans:
$7($ a)
$
\frac{(1+\sin \theta)^2+\cos ^2 \theta}{\cos \theta(1+\sin \theta)}
$
Use of $\sin ^2 \theta+\cos ^2 \theta=1 \rightarrow \frac{2+2 \sin \theta}{\cos \theta(1+\sin \theta)} \rightarrow \frac{2}{\cos \theta}$.
7 (b)
$
\frac{2}{\cos \theta}=\frac{3}{\sin \theta} \rightarrow \tan \theta=1.5
$
$\theta=0.983$ or 4.12
(FT on second value for 1 st value $+\pi$ )
Question
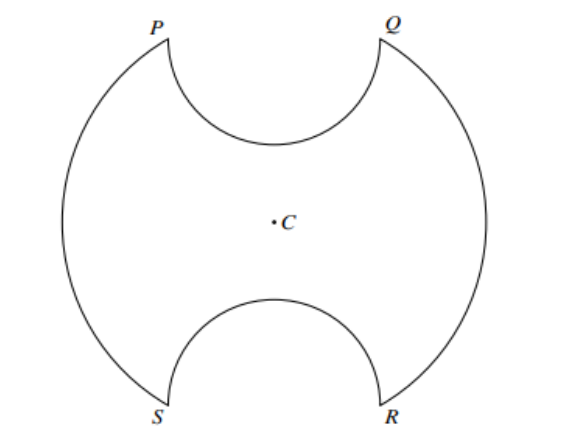
▶️Answer/Explanation
Ans:
8(a) Either Let midpoint of $P Q$ be $H$ : $\sin H C P=\frac{2}{4} \Rightarrow$ Angle $H C P=\frac{\pi}{6}$ Or $\sin P S Q=\frac{4}{8} \Rightarrow$ Angle $P S Q=\frac{\pi}{6}$
Or using cosine rule: angle $P C Q=\frac{\pi}{3}$
Or by inspection: triangle $P C Q$ or $P C T$ is equilateral so angle $P C Q=\frac{\pi}{3}$
Angle $P C S=\pi-\frac{\pi}{6}-\frac{\pi}{6}=\frac{2}{3} \pi$
8(b) $\quad$ Perimeter $=2 \times 4 \times \frac{2 \pi}{3}$ or $8 \pi-\frac{8 \pi}{3}$
$+2 \pi \times 2$
$\frac{28 \pi}{3}$
Area sector $C P Q=\frac{1}{2} \times 4^2 \times \frac{\pi}{3}=\frac{8 \pi}{3}$
Area of segment of large circle beyond $C P Q$
$
=\frac{8 \pi}{3}-\frac{1}{2} \times 4^2 \times \sin \left(\frac{\pi}{3}\right)=\frac{8 \pi}{3}-4 \sqrt{3}
$
Area of small semicircle $=\pi \times 2 \quad$ or area of small circle $=\pi \times 2^2$
Area of plate $=$ Large circle $-[2 \times]$ small semicircle $-[2 \times]$ segment area $\pi \times 4^2-\pi \times 2^2-2 \times\left(\frac{8 \pi}{3}-4 \sqrt{3}\right)=\frac{20 \pi}{3}+8 \sqrt{3}$
Alternative method for Question 8(c)
Area of sector $P C S=\frac{1}{2} \times 4^2 \times \frac{2 \pi}{3}=\frac{16 \pi}{3}$
Area of triangle $P C Q=\frac{1}{2} \times 4^2 \times \sin \frac{\pi}{3}=4 \sqrt{3}$
Area of small semicircle $=\pi \times 2 \quad$ or area of circle $=\pi \times 2^2$
Area of plate $=[2 \times]$ large sector $+[2 \times]$ triangle $-[2 \times]$ small semicircle
$
2\left(\frac{16 \pi}{3}\right)+2(4 \sqrt{3})-\pi \times 2^2=\frac{20 \pi}{3}+8 \sqrt{3}
$
Question
9 The volume $V \mathrm{~m}^3$ of a large circular mound of iron ore of radius $r \mathrm{~m}$ is modelled by the equation $V=\frac{3}{2}\left(r-\frac{1}{2}\right)^3-1$ for $r \geqslant 2$. Iron ore is added to the mound at a constant rate of $1.5 \mathrm{~m}^3$ per second.
(a) Find the rate at which the radius of the mound is increasing at the instant when the radius is $5.5 \mathrm{~m}$. [3]
(b) Find the volume of the mound at the instant when the radius is increasing at $0.1 \mathrm{~m}$ per second. [3]
▶️Answer/Explanation
Ans:
9(a)
$\left[\frac{\mathrm{d} V}{\mathrm{~d} r}=\right] \frac{9}{2}\left(r-\frac{1}{2}\right)^2$
9(b)
$\frac{\mathrm{d} r}{\mathrm{~d} t}=\frac{\mathrm{d} r}{\mathrm{~d} V} \times \frac{\mathrm{d} V}{\mathrm{~d} t}=\frac{1.5}{t h e i r \frac{\mathrm{d} V}{\mathrm{~d} r}}\left[=\frac{1.5}{\frac{9}{2}\left(5.5-\frac{1}{2}\right)^2}=\frac{1.5}{112.5}\right]$
0.0133 or $\frac{3}{225}$ or $\frac{1}{75}$ [ metres per second]
$\frac{\mathrm{d} V}{\mathrm{~d} r}$ or their $\frac{\mathrm{d} V}{\mathrm{~d} r}=\frac{1.5}{0.1}$ or 15 OR $0.1=\frac{1.5}{\text { their } \frac{\mathrm{d} V}{\mathrm{~d} r}}\left\lfloor=\frac{2 \times 1.5}{9\left(r-\frac{1}{2}\right)^2} \mathrm{OE}\right\rfloor$
$\left[\frac{9}{2}\left(r-\frac{1}{2}\right)^2=15 \Rightarrow\right] r=\frac{1}{2}+\sqrt{\frac{10}{3}}$
[Volume $=$ ] 8.13 AWRT
Question
10 The equation of a curve is such that $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=6 x^2-\frac{4}{x^3}$. The curve has a stationary point at $\left(-1, \frac{9}{2}\right)$.
(a) Determine the nature of the stationary point at $\left(-1, \frac{9}{2}\right)$. [1]
(b) Find the equation of the curve. [5]
(c) Show that the curve has no other stationary points. [3]
(d) A point $A$ is moving along the curve and the $y$-coordinate of $A$ is increasing at a rate of 5 units per second.
Find the rate of increase of the $x$-coordinate of $A$ at the point where $x=1$. [3]
▶️Answer/Explanation
Ans:
$
\text { 10(b) } \begin{aligned}
& \frac{\mathrm{d} y}{\mathrm{~d} x}=2 x^3+\frac{2}{x^2}[+c] \\
& 0=-2+2+c \text { leading to } c=[0] \\
& y=\frac{1}{2} x^4-\frac{2}{x}+(\text { their } c) x+k \\
& \frac{9}{2}=\frac{1}{2}+2+k \text { leading to } k=[2] \\
& y=\frac{1}{2} x^4-\frac{2}{x}+2
\end{aligned}
$
10(c) $\quad \frac{\mathrm{d} y}{\mathrm{~d} x}=2 x^3+\frac{2}{x^2}=0$
Leading to $x^5=-1$
So only stationary point is when $x=-1$
$10(\mathrm{~d})$
$
\begin{aligned}
& \text { At } x=1, \frac{\mathrm{d} y}{\mathrm{~d} x}=[4] \\
& \frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{\mathrm{d} x}{\mathrm{~d} y} \times \frac{\mathrm{d} y}{\mathrm{~d} t}=\frac{1}{4} \times 5 \\
& \frac{5}{4}
\end{aligned}
$
Question
11 The coordinates of points $A, B$ and $C$ are $A(5,-2), B(10,3)$ and $C(2 p, p)$, where $p$ is a constant.
(a) Given that $A C$ and $B C$ are equal in length, find the value of the fraction $p$. [3]
(b) It is now given instead that $A C$ is perpendicular to $B C$ and that $p$ is an integer.
(i) Find the value of $p$. [4]
(ii) Find the equation of the circle which passes through $A, B$ and $C$, giving your answer in the form $x^2+y^2+a x+b y+c=0$, where $a, b$ and $c$ are constants.
▶️Answer/Explanation
Ans:
11(a)
$
\begin{aligned}
& (5-2 p)^2+(p+2)^2=(10-2 p)^2+(3-p)^2 \\
& 25-20 p+4 p^2+p^2+4 p+4=100-40 p+4 p^2+9-6 p+p^2 \\
& 30 p=80 \rightarrow p=\frac{8}{3} \text { oe }
\end{aligned}
$
11 (b)(i)
$
\begin{aligned}
& m_{A C}=\frac{p+2}{2 p-5} \quad m_{B C}=\frac{p-3}{2 p-10} \\
& \frac{p+2}{2 p-5} \times \frac{p-3}{2 p-10}=-1 \\
& – \\
& p^2-p-6=-\left(4 p^2-30 p+50\right) \rightarrow 5 p^2-31 p+44 \quad(=0) \\
& \left.p=4 \text { (Ignore } p=\frac{11}{5}\right)
\end{aligned}
$
11(b)(ii) Mid-point of $A B=(71 / 2,1 / 2)$
$
r^2=2 \frac{1 / 2}{2}+2 \frac{1 / 2^2}{}\left[=\frac{50}{4}\right] \text { or } r=\sqrt{ }\left(2 \frac{1 / 2^2}{}+2 \frac{1 / 2^2}{}\right) \quad\left[=\frac{5 \sqrt{ } 2}{2}\right]
$
Equation of circle is $(x-\text { their } 71 / 2)^2+(y-\text { their } 1 / 2)^2=$ their $\frac{50}{4}$
$
x^2+y^2-15 x-y+44=0
$
Question
Find the term independent of $x$ in each of the following expansions.
(a) $\left(3 x+\frac{2}{x^{2}}\right)^6$[3]
(b) $\left(3 x+\frac{2}{x^2}\right)^6\left(1-x^3\right)$ [3]
▶️Answer/Explanation
Ans:
(a)
The term independent of $x$ will arise when the power of $x$ is zero. We need to find the term in the expansion of $\left(3 x+\frac{2}{x^2}\right)^6$ that has no $x$ term.
The general term in the binomial expansion of $(3x + \frac{2}{x^2})^6$ is given by:
$$\binom{6}{r} (3x)^{6-r}\left(\frac{2}{x^2}\right)^r$$
We want to find the value of $r$ that makes the $x$ term zero, which means that:
$$(3x)^{6-r} \left(\frac{2}{x^2}\right)^r $$
coefficient of $x^{6-3r}$ will be equivalent to zero .
$6-3r=0\Rightarrow r=2$
So, 3rd term will be independent term of the expansion $\left(3 x+\frac{2}{x^2}\right)^6$
$$\binom{6}{2} (3x)^{6-2}\left(\frac{2}{x^2}\right)^2$$
We can simplify the expression using the binomial coefficient:
$$\binom{6}{2} = \frac{6!}{2!(6-2)!} = \frac{6 \times 5}{2 \times 1} = 15$$
Next, we can simplify the powers of $3x$ and $2/x^2$:
$$(3x)^{6-2} = (3x)^4 = 81x^4$$
$$\left(\frac{2}{x^2}\right)^2 = \frac{2^2}{x^4} = \frac{4}{x^4}$$
Putting it all together, we get:
$$\binom{6}{2} (3x)^{6-2}\left(\frac{2}{x^2}\right)^2 = 15 \times 81x^4 \times \frac{4}{x^4} = 4860$$
Therefore, the value of the expression is $4860$.
(b)
To find the term independent of $x$ in this expression, we need to look for the term in the expansion of $\left(3 x+\frac{2}{x^2}\right)^6\left(1-x^3\right)$ that has no $x$ term.
To get this we will multiply the expression by $\left(1-x^3\right)$
$\underbrace{\left(3 x+\frac{2}{x^2}\right)^6 x \times (1)}_{x^0} -\underbrace{\left(3 x+\frac{2}{x^2}\right)^6 x \times (1)}_{x^{-3}}$
coefficient of $x^0$ we already calculated in (a) which is equal to $4860$ , Now we will calculate $x^{-3}$
$6-3r=-3\Rightarrow r=3$
So, 4rd term will be independent term of the expansion $\left(3 x+\frac{2}{x^2}\right)^6\left(1-x^3\right)$
$$\binom{6}{3} (3x)^{6-3}\left(\frac{2}{x^2}\right)^3[\times (-x^3)]$$
On simplifying ,$-4320$
Value of term independent will be
Question
Functions $f$ and $g$ are defined by
$
\begin{array}{ll}
\mathrm{f}(x)=4 x-2, & \text { for } x \in \mathbb{R}, \\
\mathrm{g}(x)=\frac{4}{x+1}, & \text { for } x \in \mathbb{R}, x \neq-1 .
\end{array}
$
(a) Find the value of $f g(7)$. [1]
(b) Find the values of $x$ for which $\mathrm{f}^{-1}(x)=\mathrm{g}^{-1}(x)$. [5]
▶️Answer/Explanation
Ans:
(a)
To evaluate $fg(7)$, we first need to find $g(7)$:
$$g(7) = \frac{4}{7+1} = \frac{1}{2}$$
Next, we substitute this value into $f$ to get:
$$f\left(g(7)\right) = f\left(\frac{1}{2}\right) = 4\left(\frac{1}{2}\right) – 2 = 0$$
Therefore, $fg(7) = 0$.
(b)
To find the values of $x$ for which $\mathrm{f}^{-1}(x)=\mathrm{g}^{-1}(x)$, we need to find $x$ such that $\mathrm{f}(\mathrm{f}^{-1}(x))=\mathrm{g}(\mathrm{g}^{-1}(x))=x$.
Let $y=\mathrm{f}^{-1}(x)$. Then, we have $\mathrm{f}(y)=x$, which implies $4y-2=x$. Solving for $y$, we get $y=\frac{x+2}{4}$.
Similarly, let $z=\mathrm{g}^{-1}(x)$. Then, we have $\mathrm{g}(z)=x$, which implies $\frac{4}{z+1}=x$. Solving for $z$, we get $z=\frac{4}{x}-1$.
Now, we have $\mathrm{f}^{-1}(x)=y=\frac{x+2}{4}$ and $\mathrm{g}^{-1}(x)=z=\frac{4}{x}-1$. Setting them equal to each other, we get $\frac{x+2}{4}=\frac{4}{x}-1$. Simplifying this equation, we get $x^2-2x-8=0$, which can be factored as $(x-4)(x+2)=0$. Therefore, the solutions are $x=4$ and $x=-2$.
To check that these values of $x$ satisfy the condition $\mathrm{f}(\mathrm{f}^{-1}(x))=\mathrm{g}(\mathrm{g}^{-1}(x))=x$, we substitute them into the expressions we obtained earlier for $\mathrm{f}^{-1}(x)$ and $\mathrm{g}^{-1}(x)$.
For $x=4$, we have $y=\frac{x+2}{4}=\frac{6}{4}=\frac{3}{2}$ and $z=\frac{4}{x}-1=0$, so $\mathrm{f}(\mathrm{f}^{-1}(x))=\mathrm{f}(y)=4$ and $\mathrm{g}(\mathrm{g}^{-1}(x))=\mathrm{g}(z)=4$, which satisfies the condition.
For $x=-2$, we have $y=\frac{x+2}{4}=0$ and $z=\frac{4}{x}-1=-2$, so $\mathrm{f}(\mathrm{f}^{-1}(x))=\mathrm{f}(y)=-2$ and $\mathrm{g}(\mathrm{g}^{-1}(x))=\mathrm{g}(z)=-2$, which also satisfies the condition.
Therefore, the solutions are $x=4$ and $x=-2$.
Question
A woman’s basic salary for her first year with a particular company is $\$ 30000$ and at the end of the year she also gets a bonus of $\$ 600$.
(a) For her first year, express her bonus as a percentage of her basic salary. $[1]$
At the end of each complete year, the woman’s basic salary will increase by $3 \%$ and her bonus will increase by $\$ 100$.
(b) Express the bonus she will be paid at the end of her 24th year as a percentage of the basic salary paid during that year. [5]
▶️Answer/Explanation
Ans:
(a) The bonus of $\$ 600$ is a fraction of the woman’s basic salary of $\$ 30000$. To find out what that fraction is, we can calculate:
$$\frac{\$ 600}{\$ 30000} = 0.02$$
So the bonus is $0.02$ times the basic salary. To express this as a percentage, we multiply by $100$:
$$0.02 \times 100 = 2\%$$
Therefore, the bonus of $\$ 600$ is $2\%$ of the woman’s basic salary of $\$ 30000$ for her first year.
(b)
For the basic salary, we can use the formula for the compound interest:
$$T_{24}=a(1+r)^{24}$$
where $a=30000$ is the initial amount, $r=0.03$ is the annual interest rate, and $T_{24}$ is the amount after 24 years. Plugging in the values, we get:
$$T_{24}=30000(1+0.03)^{24} \approx 59,207.60$$
So the woman’s basic salary at the end of her 24th year is approximately $\$ 59,207.60$.
For the bonus, we know that the woman receives $\$ 600$ in the first year and an additional $\$ 100$ each year thereafter. So in the 24th year, she will receive:
$$\text{bonus} = \$ 600 + (\text{number of years} – 1) \times \$ 100 = \$ 2900$$
Finally, we can express the bonus as a percentage of the basic salary in the 24th year:
$$\text{percentage} = \frac{\text{bonus}}{\text{basic salary}} \times 100\% = \frac{2900}{59,207.60} \times 100\% \approx 4.89\%$$
Therefore, the bonus of $\$ 2900$ she will be paid at the end of her 24th year is approximately $4.89\%$ of the basic salary paid during that year, which is approximately $\$ 59,207.60$.