Introduction to Three–dimensional Geometry : Notes and Study Materials -pdf
- Concepts of Introduction to Three–dimensional Geometry
- Introduction to Three–dimensional Geometry Master File
- Introduction to Three–dimensional Geometry Revision Notes
- R D Sharma Solution of Introduction to Three–dimensional Geometry
- NCERT Solution Introduction to Three–dimensional Geometry
- NCERT Exemplar Solution Introduction to Three–dimensional Geometry
- Introduction to Three–dimensional Geometry: Solved Example 1
CBSE Class 11 Maths Notes Chapter 12 Introduction to Three Dimensional Geometry
Coordinate Axes
In three dimensions, the coordinate axes of a rectangular cartesian coordinate system are three mutually perpendicular lines. These axes are called the X, Y and Z axes.
Coordinate Planes
The three planes determined by the pair of axes are the coordinate planes. These planes are called XY, YZ and ZX plane and they divide the space into eight regions known as octants.
Coordinates of a Point in Space
The coordinates of a point in the space are the perpendicular distances from P on three mutually perpendicular coordinate planes YZ, ZX, and XY respectively. The coordinates of a point P are written in the form of triplet like (x, y, z).
The coordinates of any point on
- X-axis is of the form (x, 0,0)
- Y-axis is of the form (0, y, 0)
- Z-axis is of the form (0, 0, z)
- XY-plane are of the form (x, y, 0)
- YZ-plane is of the form (0, y, z)
- ZX-plane are of the form (x, 0, z)
Distance Formula
The distance between two points P(x1, y1, z1) and Q(x2, y2, z2) is given by![]()
The distance of a point P(x, y, z) from the origin O(0, 0, 0) is given by
OP = x2+y2+z2−−−−−−−−−−√
Section Formula
The coordinates of the point R which divides the line segment joining two points P(x1, y1, z1) and Q(x2, y2, z2) internally or externally in the ratio m : n are given by
The coordinates of the mid-point of the line segment joining two points P(x1, y1, z1) and Q(x2, y2, z2) are
The coordinates of the centroid of the triangle, whose vertices are (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) are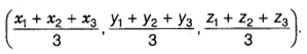
Introduction to Three Dimensional Geometry Class 11 MCQs Questions with Answers
Question 1.
The cartesian equation of the line is 3x + 1 = 6y – 2 = 1 – z then its direction ratio are
(a) 1/3, 1/6, 1
(b) -1/3, 1/6, 1
(c) 1/3, -1/6, 1
(d) 1/3, 1/6, -1
Answer
Answer: (a) 1/3, 1/6, 1
Hint:
Given 3x + 1 = 6y – 2 = 1 – z
= (3x + 1)/1 = (6y – 2)/1 = (1 – z)/1
= (x + 1/3)/(1/3) = (y – 2/6)/(1/6) = (1 – z)/1
= (x + 1/3)/(1/3) = (y – 1/3)/(1/6) = (1 – z)/1
Now, the direction ratios are: 1/3, 1/6, 1
Question 2.
The image of the point P(1, 3, 4) in the plane 2x – y + z = 0 is
(a) (-3, 5, 2)
(b) (3, 5, 2)
(c) (3, -5, 2)
(d) (3, 5, -2)
Answer
Answer: (a) (-3, 5, 2)
Hint:
Let image of the point P(1, 3, 4) is Q in the given plane.
The equation of the line through P and normal to the given plane is
(x-1)/2 = (y-3)/-1 = (z-4)/1
Since the line passes through Q, so let the coordinate of Q are (2r + 1, -r + 3, r + 4)
Now, the coordinate of the mid-point of PQ is
(r + 1, -r/2 + 3, r/2 + 4)
Now, this point lies in the given plane.
2(r + 1) – (-r/2 + 3) + (r/2 + 4) + 3 = 0
⇒ 2r + 2 + r/2 – 3 + r/2 + 4 + 3 = 0
⇒ 3r + 6 = 0
⇒ r = -2
Hence, the coordinate of Q is (2r + 1, -r + 3, r + 4) = (-4 + 1, 2 + 3, -2 + 4)
= (-3, 5, 2)
Question 3.
Three planes x + y = 0, y + z = 0, and x + z = 0
(a) none of these
(b) meet in a line
(c) meet in a unique point
(d) meet taken two at a time in parallel lines
Answer
Answer: (c) meet in a unique point
Hint:
Given, three planes are
x + y = 0 …….. 1
y + z = 0 …….. 2
and x + z = 0 ……… 3
add these planes, we get
2(x + y + z) = 0
⇒ x + y + z = 0 ……… 4
From equation 1
0 + z = 0
⇒ z = 0
From equation 2
x + 0 = 0
⇒ x = 0
From equation 3
y + 0 = 0
⇒ y = 0
So, (x, y, z) = (0, 0, 0)
Hence, the three planes meet in a unique point.
Question 4.
The coordinate of foot of perpendicular drawn from the point A(1, 0, 3) to the join of the point B(4, 7, 1) and C(3, 5, 3) are
(a) (5/3, 7/3, 17/3)
(b) (5, 7, 17)
(c) (5/3, -7/3, 17/3)
(d) (5/7, -7/3, -17/3)
Answer
Answer: (a) (5/3, 7/3, 17/3)
Hint:
Let D be the foot of perpendicular and let it divide BC in the ration m : 1
Then the coordinates of D are {(3m + 4)/(m + 1), (5m + 7)/(m + 1), (3m + 1)/(m + 1)}
Now, AD ⊥ BC
⇒ AD . BC = 0
⇒ -(2m + 3) – 2(5m + 7) – 4 = 0
⇒ m = -7/4
So, the coordinate of D are (5/3, 7/3, 17/3)
Question 5.
The locus of a point which moves so that the difference of the squares of its distances from two given points is constant, is a
(a) Straight line
(b) Plane
(c) Sphere
(d) None of these
Answer
Answer: (b) Plane
Hint:
Let the position vectors of the given points A and B be a and b respectively and that of the variable point be r.
Now, given that
PA² – PB² = k (constant)
⇒ |AP|² – |BP|² = k
⇒ |r – a|² – |r – b|² = k
⇒ (|r|² + |a|² – 2r.a) – (|r|² + |b|² – 2r.b) = k
⇒ 2r.(b – a) = k + |b|² – |a|²
⇒ r.(b – a) = (k + |b|² – |a|²)/2
⇒ r.(b – a) = C where C = (k + |b|² – |a|²)/2 = constant
So, it represents the equation of a plane.
Question 6.
The equation of the set of point P, the sum of whose distance from A(4, 0, 0) and B(-4, 0, 0) is equal to 10 is
(a) 9x² + 25y² + 25z² + 225 = 0
(b) 9x² + 25y² + 25z² – 225 = 0
(c) 9x² + 25y² – 25z² – 225 = 0
(d) 9x² – 25y² – 25z² – 225 = 0
Answer
Answer: (b) 9x² + 25y² + 25z² – 225 = 0
Hint:
Let the point P is (x, y, z)
Now given that
PA + PB = 10
⇒ √{(x-4)² + y² + z²} + √{(x+4)² + y² + z²} = 10
⇒ √{(x-4)² + y² + z²} = 10 – √{(x+4)² + y² + z²}
Now square both side
[√{(x-4)² + y² + z²}]² = (10)² + [{(x+4)² + y² + z²}]² – 2 ×10×√{(x+4)² + y² + z²}
⇒ {(x-4)² + y² + z²} = 100 + {(x+4)² + y² + z²} – 20×√{(x+4)² + y² + z²}
⇒ x² + 16 – 8x + y² + z² = 100 + x² + 16 + 8x + y² + z² – 20×√{(x+4)² + y² + z²}
⇒ – 8x = 100 + 8x – 20×√{(x+4)² + y² + z²}
⇒ -8x -8x – 100 = – 20×√{(x+4)² + y² + z²}
⇒ -16x -100 = – 20×√{(x+4)² + y² + z²}
⇒ 4x + 25 = 5×√{(x+4)² + y² + z²}
Again square both side,
(4x + 25)² = 25 ×[√{(x+4)² + y² + z²}]²
⇒ 16x² + 625 + 200x = 25×{(x+4)² + y² + z²}
⇒ 16x² + 625 + 200x = 25×(x² + 16 + 8x + y² + z²)
⇒ 16x² + 625 + 200x = 25x² + 400 + 200x + 25y² + 25z²
⇒ 25x² + 400 + 200x + 25y² + 25z² – 16x² – 625 – 200x = 0
⇒ 9x² + 25y² + 25z² – 225 = 0
Question 7.
The maximum distance between points (3sin θ, 0, 0) and (4cos θ, 0, 0) is
(a) 3
(b) 4
(c) 5
(d) Can not be find
Answer
Answer: (c) 5
Hint:
Given two points are (3sin θ, 0, 0) and (4cos θ, 0, 0)
Now distance = √{(4cos θ – 3sin θ)² + (0 – 0)² + (0 – 0)²}
⇒ distance = √{(4cos θ – 3sin θ)²}
⇒ distance = 4cos θ – 3sin θ ……………. 1
Now, maximum value of 4cos θ – 3sin θ = √{(4² + (-3)²}
= √(16 + 9)
= √25
= 5
From equation 1, we get
distance = 5
So, the maximum distance between points (3sin θ, 0, 0) and (4cos θ, 0, 0) is 5
Question 8.
A vector r is equally inclined with the coordinate axes. If the tip of r is in the positive octant and |r| = 6, then r is
(a) 2√3(i – j + k)
(b) 2√3(-i + j + k)
(c) 2√3(i + j – k)
(d) 2√3(i + j + k)
Answer
Answer: (d) 2√3(i + j + k)
Hint:
Let l, m, n are DCs of r.
Given, l = m = n
⇒ l² + m² + n² = 1
⇒ 3l² = 1
⇒ l² = 1/3
⇒ l = m = n = 1/√3
So, r = |r|(li + mj + nk)
⇒ r = 6(i/√3 + j/√3 + k/√3)
⇒ r = 2√3(i + j + k)
Question 9.
The plane 2x – (1 + a)y + 3az = 0 passes through the intersection of the planes
2x – y = 0 and y + 3z = 0
2x – y = 0 and y – 3z = 0
2x + 3z = 0 and y = 0
2x – 3z = 0 and y = 0
Answer
Answer: (d) A
Hint:
Given, equation of plane is:
2x – (1 + a)y + 3az = 0
=> (2x – y) + a(-y + 3z) = 0
which is passing through the intersection of the planes
2x – y = 0 and -y + 3z = 0
2x – y = 0 and y – 3z = 0
Question 10.
If the end points of a diagonal of a square are (1, -2, 3) and (2, -3, 5) then the length of the side of square is
(a) √3 unit
(b) 2√3 unit
(c) 3√3 unit
(d) 4√3 unit
Answer
Answer: (a) √3 unit
Hint:
Let a is the length of the side of a square.
Given, the diagonal of a square are (1,–2,3) and (2, -3, 5)
Now, length of the diagonal of square = √{(1 – 2)² + (-2 + 3)² + (3 – 5)²}
= √{1 + 1 + 4}
= √6
Again length of the diagonal of square is √2 times the length of side of the square.
⇒ a√2 = √6
⇒ a√2 = √3×√2
⇒ a = √3
So, the length of side of square is √3 unit
Question 11.
The coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the YZ plane is
(a) (0, 17/2, 13/2)
(b) (0, -17/2, -13/2)
(c) (0, 17/2, -13/2)
(d) None of these
Answer
Answer: (c) (0, 17/2, -13/2)
Hint:
The line passing through the points (5, 1, 6) and (3, 4, 1) is given as
(x-5)/(3-5) = (y-1)/(4-1) = (z-6)/(1-6)
⇒ (x-5)/(-2) = (y-1)/3 = (z-6)/(-5) = k(say)
⇒ (x-5)/(-2) = k
⇒ x – 5 = -2k
⇒ x = 5 – 2k
(y-1)/3 = k
⇒ y – 1 = 3k
⇒ y = 3k + 1
and (z-6)/(-5) = k
⇒ z – 6 = -5k
⇒ z = 6 – 5k
Now, any point on the line is of the form (5 – 2k, 3k + 1, 6 – 5k)
The equation of YZ-plane is x = 0
Since the line passes through YZ-plane
So, 5 – 2k = 0
⇒ k = 5/2
Now, 3k + 1 = 3 × 5/2 + 1 = 15/2 + 1 = 17/2
and 6 – 5k = 6 – 5×5/2 = 6 – 25/2 = -13/2
Hence, the required point is (0, 17/2, -13/2)
Question 12.
The angle between the vectors with direction ratios are 4, -3, 5 and 3, 4, 5 is
(a) π/2
(b) π/3
(c) π/4
(d) π/6
Answer
Answer: (b) π/3
Hint:
Let a is a vector parallel to the vector having direction ratio is 4, -3, 5
⇒ a = 4i – 3j + 5k
Let b is a vector parallel to the vector having direction ratio is 3 ,4, 5
⇒ b = 3i + 4j + 5k
Let θ be the angle between the given vectors.
Now, cos θ = (a . b)/(|a|×|b|)
⇒ cos θ = (12 – 12 + 25)/{√(16 + 9 + 25)×√(9 + 16 + 25)}
⇒ cos θ = 25/{√(50)×√(50)}
⇒ cos θ = 25/50
⇒ cos θ = 1/2
⇒ cos θ = π/3
⇒ θ = π/3
So, the angle between the vectors with direction ratios are 4, -3, 5 and 3, 4, 5 is π/3
Question 13.
The equation of plane passing through the point i + j + k and parallel to the plane r . (2i – j + 2k) = 5 is
(a) r . (2i – j + 2k) = 2
(b) r . (2i – j + 2k) = 3
(c) r . (2i – j + 2k) = 4
(d) r . (2i – j + 2k) = 5
Answer
Answer: (b) r . (2i – j + 2k) = 3
Hint:
The equation of plane parallel to the plane r . (2i – j + 2k) = 5 is
r . (2i – j + 2k) = d
Since it passes through the point i + j + k, therefore
(i + j + k) . (2i – j + 2k) = d
⇒ d = 2 – 1 + 2
⇒ d = 3
So, the required equation of the plane is
r . (2i – j + 2k) = 3
Question 14.
A vector r is equally inclined with the coordinate axes. If the tip of r is in the positive octant and |r| = 6, then r is
(a) 2√3(i – j + k)
(b) 2√3(-i + j + k)
(c) 2√3(i + j – k)
(d) 2√3(i + j + k)
Answer
Answer: (d) 2√3(i + j + k)
Hint:
Let l, m, n are DCs of r.
Given, l = m = n
⇒ l² + m² + n² = 1
⇒ 3l² = 1
⇒ l² = 1/3
⇒ l = m = n = 1/√3
So, r = |r|(li + mj + nk)
⇒ r = 6(i/√3 + j/√3 + k/√3)
⇒ r = 2√3(i + j + k)
Question 15.
The maximum distance between points (3sin θ, 0, 0) and (4cos θ, 0, 0) is
(a) 3
(b) 4
(c) 5
(d) Can not be find
Answer
Answer: (c) 5
Hint:
Given two points are (3sin θ, 0, 0) and (4cos θ, 0, 0)
Now distance = √{(4cos θ – 3sin θ)² + (0 – 0)² + (0 – 0)²}
⇒ distance = √{(4cos θ – 3sin θ)²}
⇒ distance = 4cos θ – 3sin θ …………….1
Now, maximum value of 4cos θ – 3sin θ = √{(4² + (-3)²}
= √(16 + 9)
= √25
= 5
From equation 1, we get
distance = 5
So, the maximum distance between points (3sin θ, 0, 0) and (4cos θ, 0, 0) is 5
Question 16.
The image of the point P(1, 3, 4) in the plane 2x – y + z = 0 is
(a) (-3, 5, 2)
(b) (3, 5, 2)
(c) (3, -5, 2)
(d) (3, 5, -2)
Answer
Answer: (a) (-3, 5, 2)
Hint:
Let image of the point P(1, 3, 4) is Q in the given plane.
The equation of the line through P and normal to the given plane is
(x-1)/2 = (y-3)/-1 = (z-4)/1
Since the line passes through Q, so let the coordinate of Q are (2r + 1, -r + 3, r + 4)
Now, the coordinate of the mid-point of PQ is
(r + 1, -r/2 + 3, r/2 + 4)
Now, this point lies in the given plane.
2(r + 1) – (-r/2 + 3) + (r/2 + 4) + 3 = 0
⇒ 2r + 2 + r/2 – 3 + r/2 + 4 + 3 = 0
⇒ 3r + 6 = 0
⇒ r = -2
Hence, the coordinate of Q is (2r + 1, -r + 3, r + 4) = (-4 + 1, 2 + 3, -2 + 4)
= (-3, 5, 2)
Question 17.
The points on the y- axis which are at a distance of 3 units from the point (2, 3, -1) is
(a) either (0, -1, 0) or (0, -7, 0)
(b) either (0, 1, 0) or (0, 7, 0)
(c) either (0, 1, 0) or (0, -7, 0)
(d) either (0, -1, 0) or (0, 7, 0)
Answer
Answer: (d) either (0, -1, 0) or (0, 7, 0)
Hint:
Let the point on y-axis is O(0, y, 0)
Given point is A(2, 3, -1)
Given OA = 3
⇒ OA² = 9
⇒ (2 – 0)² + (3 – y)² + (-1 – 0)² = 9
⇒ 4 + (3 – y)² + 1 = 9
⇒ 5 + (3 – y)² = 9
⇒ (3 – y)² = 9 – 5
⇒ (3 – y)² = 4
⇒ 3 – y = √4
⇒ 3 – y = ±4
⇒ 3 – y = 4 and 3 – y = -4
⇒ y = -1, 7
So, the point is either (0, -1, 0) or (0, 7, 0)
Question 18.
If α, β, γ are the angles made by a half ray of a line respectively with positive directions of X-axis Y-axis and Z-axis, then sin² α + sin² β + sin² γ =
(a) 1
(b) 0
(c) -1
(d) None of these
Answer
Answer: (d) None of these
Hint:
Let l, m, n be the direction cosines of the given vector.
Then, α, β, γ
l = cos α
m = cos β
n = cos γ
Now, l² + m² + n² = 1
⇒ cos² α + cos² β + cos² γ = 1
⇒ 1 – sin² α + 1 – sin² β + 1 – sin² γ = 1
⇒ 3 – sin² α – sin² β – sin² γ = 1
⇒ 3 – 1 = sin² α + sin² β + sin² γ
⇒ sin² α + sin² β + sin² γ = 2
Question 19.
If P(x, y, z) is a point on the line segment joining Q(2, 2, 4) and R(3, 5, 6) such that the projections of OP on the axes are 13/5, 19/5, 26/5 respectively, then P divides QR in the ration
(a) 1 : 2
(b) 3 : 2
(c) 2 : 3
(d) 1 : 3
Answer
Answer: (b) 3 : 2
Hint:
Since OP has projections 13/5, 19/5 and 26/5 on the coordinate axes, therefore
OP = 13i/5 + 19j/5 + 26/5k
Let P divides the join of Q(2, 2, 4) and R(3, 5, 6) in the ratio m : 1
Then the position vector of P is
{(3m + 2)/(m + 1), (5m + 2)/(m + 1), (6m + 4)/(m + 1)}
So, 13i/5 + 19j/5 + 26/5k = (3m + 2)/(m + 1)+ (5m + 2)/(m + 1)+ (6m + 4)/(m + 1)
⇒ (3m + 2)/(m + 1) = 13/5
⇒ 2m = 3
⇒ m = 3/2
⇒ m : 1 = 3 : 2
Hence, P divides QR in the ration 3 : 2
Question 20.
In a three dimensional space, the equation 3x – 4y = 0 represents
(a) a plane containing Y axis
(b) none of these
(c) a plane containing Z axis
(d) a plane containing X axis
Answer
Answer: (c) a plane containing Z axis
Hint:
Given, equation is 3x – 4y = 0
Here z = 0
So, the given equation 3x – 4y = 0 represents a plane containing Z axis.