what is probability
Probability is the measure of the likeliness that an event will occur. Probability is quantified as a number between 0 and 1 (where 0 indicates impossibility and 1 indicates certainty)
Why we need Probability and what is the use of it?
It is widely used in the study of Mathematics, Statistics, Gambling, Physical sciences, Biological sciences, Weather forecasting, Finance etc. to draw conclusions. Insurance companies uses this to decide on financial policies
Terms related to Probability
Randomness or Random experiments
- When we perform experiments in science and engineering repeatedly under very nearly identical conditions, we almost get the same result.
- Such experiments are called deterministic experiments.
- There also exists experiments When next outcome of the experiment cannot be determined even they are performed under nearly identical conditions then we say it is a random experiment
e.g. Consider the dice. When we throw the dice, we cannot determine what number will come Since we cannot predict the next outcome, we may say it is a random experiment
- Probability theory is concerned with such random phenomena or random experiments
Trial
A trial is an action which results in one or several outcomes, for example each toss of the coin and each throw of the die are called trials
Independent Trial
Successive trials of some random event for example tosses of a coin,throws of a die are said to be independent if the outcome of any one trial does not impact the outcomes of any others.
Sample space
- It is a set of all possible outcomes of an random experiment which we defined earliar
e.g. when we coin is tossed, the possible outcome are Head and Tail.So sample space is Head and tail - It is generally denoted by letter S
- The sample space can be either be finite or infinite.
- It is a set of all possible outcomes of an random experiment which we defined earliar
Example for infinite Sample space would be an experiment where we are tossing the coin until Head comes up.
- Sample space { (H), (TH),(TTH), (TTTH)..}
- We can use Tree diagram to find out the sample space. Permutation and combination studied in earliar chapter also will be used extensively to find the sample space
Elementary event
Each outcome of the random experiment is known as elementary events
Event
- An event is a possible outcome of the Experiment. Any subset E of the sample space S is called an event.
- Example of events
1. Roll a die: the outcome is even {2, 4, 6}.
2. Flip a coin twice and the two results are different:
{(H, T),(T, H)}.
Different type of events
| Elementary or simple event | If it contains the single elements of the sample space |
| Compound event | If it contains more than single elements of the sample space |
| Impossible event | If it can never occur. |
| Sure or certain event | An event which is sure to occur |
Algebra of events operations
We know the event are sets and they are subset of Sample space. So normal set operations can be done over them also
Let A and B are two events of the Sample Space S
| Union: (A ∪ B) an outcome is in A ∪ B if it is either in A or in B. | 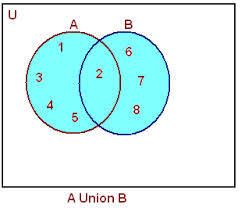 |
| Intersection: (A ∩ B), AB: an outcome is in AB if it is in both A and B. | 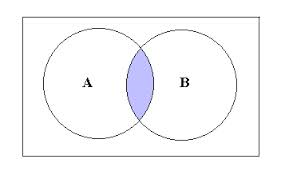 |
| Difference (A -B) , the event of occurrence of A but not B | 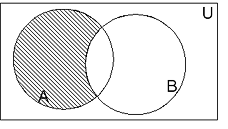 |
| Difference (B -A) , the event of occurrence of B but not A | |
| AC : The event of non-occurrence of the event A.It is also called the complementary event of A |
Some More Important Definition on Probability
Equally Likely Outcomes
The outcome of the random experiments are called equally likely outcomes. If all of them are equal preferences.
Exhaustive Outcomes
The outcome of the random experiments are called exhaustive outcomes. If they cover all the possible outcomes of the experiments
Theoretical probability definition or Classical Probability
The theoretical probability or the classical probability of the event A in a random experiment having exhaustive, equal likely outcome is defined as
- Let Number of exhaustive equally likely cases of the experiment =n
Number of outcome favorable to A=m
Then
$P( A) = \frac {m}{n}$
Also you may have observed that
$ 0 \leq m \leq n$
Or
$ 0 \leq \frac {m}{n} \leq 1$ - The event $A^c$ representing ‘not A’, is called the complement of the event A. We also say that $A^c$ and $A$ are complementary events.
Now
$P(A^c) = \frac {n-m}{n} = 1 – \frac {m}{n} = 1- P(A)$
Or
$P(A) +P(A^c)=1$ - The probability of an event (U) which is impossible to occur is 0. Such an event is called an impossible event
$P(U)=0$ - The probability of an event ( X) which is sure (or certain) to occur is 1. Such an event is called a sure event or a certain event
$P(X)=1$
/li> - Probability of any event can be as
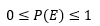
- Odds in favor of the happening of the event is defined as ratio of P(A) and P(Ac/sup>)
Let it be m: n
Then $ \frac {P(A)} {P(A^c)}=\frac { m}{n}$
Or
$\frac {P(A)}{1- P(A)} =\frac {m}{n}$
Or
$P(A) = \frac {m}{(m + n)}$ - Odds against the happening of the event is defined as ratio of P(Ac) and P(A)
Let it be m: n
Then
$P(A) =\frac {n}{ (m + n)}$
How to Solve Probability Problems
- Find out the number of elements in the sample space S of the given random experiment. It would be nice to write sample space elements also if possible
- Find out the elements which lies in the event (A) which we are looking to find probability. Count the elements in it
- Both the step 1 and step 2 depends on the complexity of the problem. We may have to use Permutation and combination for arrangement questions
- Use classical definition of probability to find out the answer
Addition Theorems on Probability
- Let E and F are two events of an random experiments
Then
$P(E \cup F) = P(E) + P(F) – P(E \cap F) $
I event E and F are mutually exclusive
$n( E \cap F) =0$
Then
$P(E \cup F) = P(E) + P(F)$ - Addition Theorem of three events
Let E ,F and G are three events of an random experiments
$P(E \cup F \cup G ) = P(E) + P(F) + P(G) – P(E \cap F) – P(F \cap G) – P(E \cap G ) + P(E \cap F \cap G)$
If event E , F and G are mutually exclusive
$n( E \cap F) = 0$
$n(E \cap G) = 0$
$n(F \cap G) = 0$
$n(E \cap F \cap G)= 0$
Then
$P(E \cup F\cup G ) = P(E) + P(F) + P(G)$ - Let E and F are two events of an random experiments
Then
Probability of the occurrence of the Event E only $( E \cap F^c)$
$ P(E \cap F^c) = P(E) – P(E \cap F )$
Probability of the occurrence of the Event F only $( E^c \cap F)$
$P(E^c \cap F) = P(F) – P(E \cap F )$
Probability of occurrence of exactly one of the two event E and F
$P[(E^c \cap F) \cup (E \cap F^c) ] = P(E) + P(F) – 2 P(E \cap F)$
Solved examples
Example 1E, F and G are events associated with a random experiment such that
$P(E) = 0.3, P(F) = 0.4, P(G) = 0.8$ $P(E \cap F) = 0.08 ,P( E \cap G) = 0.28 \; and \; P(E \cap F \cap G) = 0.09$. If $P(E \cup F \cup G) \geq 0.75$ then prove that $P(F \cap G)$ lies in the interval [0.23, 0.48]
Answer
We know that
$P(E \cup F \cup G ) = P(E) + P(F) + P(G) – P(E \cap F) $
$- P(F \cap G) – P(E \cap G ) + P(E \cap F \cap G)$
$P(E \cup F \cup G ) = .3 +.4+.8 -.08-.28 +.09 – P(F \cap G)$
$P(E \cup F \cup G ) =1.23 – P(F \cap G)$ -(1) Or
$1.23 – P(F \cap G) \geq 0.75$
$1.23 -.75 \geq P(F \cap G)$
$.48 \geq P(F \cap G) $
Now we know any Probability is less than 1
So
$P(E \cup F \cup G ) \leq 1$
So
$1.23 – P(F \cap G) \leq 1$
Then
$P(F \cap G) \geq .23$
So
$.23 \leq P(F \cap G) \leq .48$
Example 2
From a pack of 52 cards, two cards are drawn together, what is the probability that both the cards are kings
Answer
Total outcome = 52C2 = 1326
Total King cases =4C2 =6
Probability ==6/1326=1/221
Example 3
Three unbiased coins are tossed. What is the probability of getting at most two heads?
Answer
S={TTT,TTH,THT,HTT,THH,HTH,HHT,HHH}
Let E be the event of getting at most two heads
E={TTT,TTH,THT,HTT,THH,HTH,HHT}
P(E) =7/8
Example 4
Find the probability of selecting a red card or a 7 from a deck of 52 cards?
Answer
We need to find out P(R or 7)
Probability of selecting a RED card=P(R) = $\frac {26}{52}$
Probability of selecting a 7 =P(7) = $\frac {4}{52}$
Probability of selecting both a red card and a 7
$P( R \cap 7) = \frac {2}{52}$
Now $P(R \cup 7) = P(R) + P(7) – P(R \cap 7)$
$= \frac {26}{52} + \frac {4}{52} – \frac {2}{52}$
$= \frac {28}{52}$
Probability Class 11 MCQs Questions with Answers
Question 1.
Two cards from a pack of 52 cards are lost. One card is drawn from the remaining cards. If drawn card is diamond then the probability that the lost cards were both hearts is
(a) 143/1176
(b) 143/11760
(c) 143/11706
(d) 134/11760
Answer
Answer: (b) 143/11760
Hint:
Total number of cards = 52
Two cards are lost.
So remaining cards = 50
Now one card is drawn.
Probability that it is a diamond card = 13/50
Now probability that both lost cards are heart = 13/50 ×(11C2 / 49C2)
= 13/50 ×[{(11×10)/2}/{(49×48/2)}]
= 13/50 ×{(11×10)/(49×48)}
= {(13×11×10)/(50×49×48)}
= {(13×11)/(5×49×48)}
= 143/11760
So probability that both lost card are heart = 143/11760
Question 2.
If four whole numbers taken at random are multiplied together, then the chance that the last digit in the product is 1, 3, 5, 7 is
(a) 16/25
(b) 16/125
(c) 16/625
(d) none of these
Answer
Answer: (c) 16/625
Hint:
The last digit of the four whole number can be
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
The chance that any of the four numbers is divisible by 2 or 5 = 6/10 = 3/5
Hence, the chance that any of the four numbers is not divisible by 2 or 5 = 1 – 3/5 = 2/5
So, the chance that all of the four numbers are divisible by 2 or 5 = (2/5)×(2/5)×(2/5)×(2/5)
= 16/625
This is the chance that the last digit in the product will not be 0, 2, 4, 5, 6, 8 and this is also the chance that the last digit in the product is 1, 3, 7 or 9
Question 3.
Three identical dice are rolled. The probability that the same number will appear on each of them is
(a) 1/6
(b) 1/36
(c) 1/18
(d) 3/28
Answer
Answer: (b) 1/36
Hint:
Total number of cases = 6³ = 216
The same number can appear on each of the dice in the following ways:
(1, 1, 1), (2, 2, 2), ………….(3, 3, 3)
So, favourable number of cases = 6
Hence, required probability = 6/216 = 1/36
Question 4.
There are four machines and it is known that exactly two of them are faulty. They are tested, one by one, in a random order till both the faulty machines are identified. Then the probability that only two tests are needed is
(a) 1/3
(b) 1/6
(c) 1/2
(d) 1/4
Answer
Answer: (b) 1/6
Hint:
First, we choose 1 machine out of given 4.
The probability that it is fault = 2/4 = 1/2
Now, we have to pick the second fault machine.
The probability that it is fault = 1/3
So, required probability = (1/2)×(1/3) = 1/6
Question 5.
Two unbiased dice are thrown. The probability that neither a doublet nor a total of 10 will appear is
(a) 3/5
(b) 2/7
(c) 5/7
(d) 7/9
Answer
Answer: (d) 7/9
Hint:
When two dice are throw, then Total outcome = 36
A doublet: {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
Favourable outcome = 6
Sum is 10: {(4, 6), (5, 5), (6, 4)}
Favourable outcome = 3
Again, A doublet and sum is 10: (5, 5)
Favourable outcome = 1
Now, P(either dublet or a sum of 10 appears) = P(A dublet appear) + P(sum is 10) – P(A dublet appear and sum is 10)
⇒ P(either dublet or a sum of 10 appears) = 6/36 + 3/36 – 1/36
= (6 + 3 – 1)/36
= 8/36
= 2/9
So, P(neither dublet nor a sum of 10 appears) = 1 – 2/9 = 7/9
Question 6.
Two dice are thrown the events A, B, C are as follows A: Getting an odd number on the first die. B: Getting a total of 7 on the two dice. C: Getting a total of greater than or equal to 8 on the two dice. Then AUB is equal to
(a) 15
(b) 17
(c) 19
(d) 21
Answer
Answer: (d) 21
Hint:
When two dice are thrown, then total outcome = 6×6 = 36
A: Getting an odd number on the first die.
A = {(1, 1), (1, 2), (1, 3), (1, 4),(1, 5), (1, 6), (3, 1), (3, 2), (3, 3), (3, 4),(3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4),(5, 5), (5, 6)}
Total outcome = 18
B: Getting a total of 7 on the two dice.
B = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
Total outcome = 6
C: Getting a total of greater than or equal to 8 on the two dice.
C = {(2, 6), (3, 5), (3, 6), (4, 4),(4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (5, 6),(6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
Total outcome = 15
Now n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
⇒ n(A ∪ B) = 18 + 6 – 3
⇒ n(A ∪ B) = 21
Question 7.
Two numbers are chosen from {1, 2, 3, 4, 5, 6} one after another without replacement. Find the probability that the smaller of the two is less than 4.
(a) 4/5
(b) 1/15
(c) 1/5
(d) 14/15
Answer
Answer: (a) 4/5
Hint:
Total number of ways of choosing two numbers out of six = 6C2 = (6×5)/2 = 3×5 = 15
If smaller number is chosen as 3 then greater has choice are 4, 5, 6
So, total choices = 3
If smaller number is chosen as 2 then greater has choice are 3, 4, 5, 6
So, total choices = 4
If smaller number is chosen as 1 then greater has choice are 2, 3, 4, 5, 6
So, total choices = 5
Total favourable case = 3 + 4 + 5 = 12
Now, required probability = 12/15 = 4/5
Question 8.
The probability that when a hand of 7 cards is drawn from a well-shuffled deck of 52 cards, it contains 3 Kings is
(a) 1/221
(b) 5/716
(c) 9/1547
(d) None of these
Answer
Answer: (c) 9/1547
Hint:
Total number of cards = 52
Number of king card = 4
Now, 7 cards are drawn from 52 cards.
P (3 cards are king) = {4C3 × 48C4}/52C7
= {4×(48×47×46×45)/(4×3×2×1)}/{(52×51×50×49×48×47×46)/(7×6×5×4×3×2×1)}
= {4×(48×47×46×45)×(7×6×5×4×3×2×1)}/{(4×3×2×1)×{(52×51×50×49×48×47×46)}
= (7×6×5×4×45)/(52×51×50×49)
= (6×5×4×45)/(52×51×50×7)
= (6×4×45)/(7×52×51×10)
= (6×45)/(7×13×51×10)
= (6×3)/(7×13×17×2)
= (3×3)/(7×13×17)
= 9/1547
Question 9.
A certain company sells tractors which fail at a rate of 1 out of 1000. If 500 tractors are purchased from this company, what is the probability of 2 of them failing within first year
(a) e-1/2/2
(b) e-1/2/4
(c) e-1/2/8
(d) none of these
Answer
Answer: (c) e-1/2/8
Hint:
This question is based on Poisson distribution.
Now, λ = np = 500×(1/1000) = 500/1000 = 1/2
Now, P(x = 2) = {e-1/2 × (1/2)²}/2! = e-1/2/(4×2) = e-1/2/8
Question 10.
The probability that in a random arrangement of the letters of the word INSTITUTION the three T are together is
(a) 0.554
(b) 0.0554
(c) 0.545
(d) 0.0545
Answer
Answer: (d) 0.0545
Hint:
Given word: INSTITUTION
Total letters = 11
The word contains 3 I, 2 N, 1 S, 3 T, 1 U and 1 O
Total number of arrangement = 11!/(3!×2!×3!) = 554400
Now, taken 3 T are together.
So total latter = 9
The number of favorable cases = 9!/(3!×2!) = 30240
Now, P(3 T are together) = 30240/554400 = 0.0545
Question 11.
Three houses are available in a locality. Three persons apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house is
(a) 2/9
(b) 1/9
(c) 8/9
(d) 7/9
Answer
Answer: (b) 1/9
Hint:
One person can select one house out of 3 = 3C1 = 3
So, three persons can select one house out of three = 3×3×3 = 27
Thus, probability that all the three can apply for the same house = 3/27 = 1/9
Question 12.
A bag contains 5 brown and 4 white socks . A man pulls out two socks. The probability that both the socks are of the same colour is
(a) 9/20
(b) 2/9
(c) 3/20
(d) 4/9
Answer
Answer: (d) 4/9
Hint:
Total number of shocks = 5 + 4 = 9
Two shocks are pulled.
Now, P(Both are same color) = (5C2 + 4C2)/9C2
= {(5×4)/(2×1) + (4×3)/(2×1)}/{(9×8)/(2×1)}
= {(5×4) + (4×3)/}/{(9×8)
= (5 + 3)/(9×2)
= 8/18
= 4/9
Question 13.
When a coin is tossed 8 times getting a head is a success. Then the probability that at least 2 heads will occur is
(a) 247/265
(b) 73/256
(c) 247/256
(d) 27/256
Answer
Answer: (c) 247/256
Hint:
Let x be number a discrete random variable which denotes the number of heads obtained in n (in this question n = 8)
The general form for probability of random variable x is
P(X = x) = nCx × px × qn-x
Now, in the question, we want at least two heads
Now, p = q = 1/2
So, P(X ≥ 2) = 8C2 × (1/2)² × (1/2)8-2
⇒ P(X ≥ 2) = 8C2 × (1/2)² × (1/2)6
⇒ 1 – P(X < 2) = 8C0 × (1/2)0 × (1/2)8 + 8C1 × (1/2)1 × (1/2)8-1
⇒ 1 – P(X < 2) = (1/2)8 + 8 × (1/2)1 × (1/2)7
⇒ 1 – P(X < 2) = 1/256 + 8 × (1/2)8
⇒ 1 – P(X < 2) = 1/256 + 8/256
⇒ 1 – P(X < 2) = 9/256
⇒ P(X < 2) = 1 – 9/256
⇒ P(X < 2) = (256 – 9)/256
⇒ P(X < 2) = 247/256
Question 14.
A couple has two children. The probability that both children are females if it is known that the elder child is a female is
(a) 0
(b) 1
(c) 1/2
(d) 1/3
Answer
Answer: (c) 1/2
Hint:
Given, a couple has two children.
Let A denotes both children are females i.e. {FF}
Now, P(A) = (1/2)×(1/2) = 1/4
and B denotes elder children is a female i.e. {FF, FM}
P(B) = 1/4 + 1/4 = 1/2
Now, P(A ∩ B) = 1/4
Now, P(Both the children are female if elder child is female)
P(A/B) = P(A ∩ B)/P(B)
⇒ P(A/B) = (1/4)/(1/2)
⇒ P(A/B) = 1/2
Question 15.
A certain company sells tractors which fail at a rate of 1 out of 1000. If 500 tractors are purchased from this company, what is the probability of 2 of them failing within first year
(a) e-1/2/2
(b) e--1/2/4
(c) e-1/2/8
(d) none of these
Answer
Answer: (c) e-1/2/8
Hint:
This question is based on Poisson distribution.
Now, λ = np = 500×(1/1000) = 500/1000 = 1/2
Now, P(x = 2) = {e-1/2 × (1/2)²}/2! = e-1/2 /(4×2) = e-1/2/8
Question 16.
A random variable X has poison distribution with mean 2. Then, P (X > 1.5) equals
(a) 1 – 3/e²
(b) 2/e²
(c) 3/e²
(d) 0
Answer
Answer: (a) 1 – 3/e²
Hint:
Here m = 2
Now, P(X > 1.5) = ∑r {(e-2 × 2r)/r!} {2 ≤ r ≤ ∞}
= e-2 {2²/2! + 2³/3! + 24/4! + …}
= e-2 {(1 + 2 /1! + 2²/2! + 2³/3! + …) – 1 – 2}
= e-2 (e² – 3)
= 1 – 3e-2
= 1 – 3/e²
Question 17.
Let A and B are two mutually exclusive events and if P(A) = 0.5 and P(B ̅) = 0.6 then P(A∪B) is
(a) 0
(b) 1
(c) 0.6
(d) 0.9
Answer
Answer: (d) 0.9
Hint:
Given, A and B are two mutually exclusive events.
So, P(A ∩ B) = 0
Again given P(A) = 0.5 and P(B ̅) = 0.6
P(B) = 1 – P(B ̅) = 1 – 0.6 = 0.4
Now, P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ P(A ∪ B) = P(A) + P(B)
⇒ P(A ∪ B) = 0.5 + 0.4 = 0.9
Question 18.
The probability of getting 53 Sundays in a leap year is
(a) 1/7
(b) 2/7
(c) 3/7
(d) None of these
Answer
Answer: (b) 2/7
Hint:
In a leap year, the total number of days = 366 days.
In 366 days, there are 52 weeks and 2 days.
Now two days may be
(i) Sunday and Monday
(ii) Monday and Tuesday
(iii) Tuesday and Wednesday
(iv) Wednesday and Thursday
(v) Thursday and Friday
(vi) Friday and Saturday
(vii) Saturday and Sunday
Now there are total 7 possibilities, So total outcomes = 7
In 7 possibilities, Sunday came two times.
So, favorable case = 2
Hence, the probabilities of getting 53 Sundays in a leap year = 2/7
Question 19.
The probability of getting the number 6 at least once in a regular die if it can roll it 6 times?
(a) 1 – (5/6)6
(b) 1 – (1/6)6
(c) (5/6)6
(d) (1/6)6
Answer
Answer: (a) 1 – (5/6)6
Hint:
Let A is the event that 6 does not occur at all.
Now, the probability of at least one 6 occur = 1 – P(A)
= 1 – (5/6)6
Question 20.
On his vacation, Rahul visits four cities (A, B, C, and D) in a random order. The probability that he visits A first and B last is
(a) 1/2
(b) 1/6
(c) 1/10
(d) 1/12
Answer
Answer: (d) 1/12
Hint:
Total cities are 4 i.e. A, B, C, D
Given, Rahul visit four cities, So, n(S) = 4! = 24
Now, sample space IS:
S = {ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BDAC, BDCA, BCAD, BCDA, CABD, CADB, CBDA, CDAD, CDAB,CDBA, DABC, DACB, DBCA, DBAC, DCAB, DCBA}
Let G = Rahul visits A firsta and B last
⇒ G = {ACDB, ADCB}
⇒ n(G) = 2
So, P(G) = n(G)/n(S) = 2/24 = 1/12