Linear Inequalities : Notes and Study Materials -pdf
CBSE Class 11 Maths Notes Chapter 6 Linear Inequalities
Inequation
A statement involving variables and the sign of inequality viz. >, <, ≥ or ≤ is called an inequation or an inequality.
Numerical Inequalities
Inequalities which do not contain any variable is called numerical inequalities, e.g. 3 < 7, 2 ≥ -1, etc. Literal Inequalities Inequalities which contains variables are called literal inequalities e.g. x – y > 0, x > 5, etc.
Linear Inequation of One Variable
Let a be non-zero real number and x be a variable. Then, inequalities of the form ax + b > 0, ax + b < 0, ax + b ≥ 0 and ax + b ≤ 0 are known as linear inequalities in one variable.
Linear Inequation of Two Variables
Let a, b be non-zero real numbers and x, y be variables. Then, inequation of the form ax + by < c, ax + by > c, ax + by ≤ c and ax + by ≥ c are known as linear inequalities in two variables x and y.
Solution of an Inequality
The value(s) of the variable(s) which makes the inequality a true statement is called its solutions. The set of all solutions of an inequality is called the solution set of the inequality.
Solving Linear Inequations in One Variable
Same number may be added (or subtracted) to both sides of an inequation without changing the sign of inequality.
Both sides of an inequation can be multiplied (or divided) by the same positive real number without changing the sign of inequality. However, the sign of inequality is reversed when both sides of an inequation are multiplied or divided by a negative number.
Representation of Solution of Linear Inequality in One Variable on a Number Line
To represent the solution of a linear inequality in one variable on a number line. We use the following algorithm.
If the inequality involves ‘>’ or ‘<‘ we draw an open circle (O) on the number line, which indicates that the number corresponding to the open circle is not included in the solution set.
If the inequality involves ‘≥’ or ‘≤’ we draw a dark circle (•) on the number line, which indicates the number corresponding to the dark circle is included in the solution set.
Graphical Representation of the Solution of Linear Inequality in One or Two Variables
To represent the solution of linear inequality in one or two variables graphically in a plane, we use the following algorithm.
If the inequality involves ‘<’ or ‘>’, we draw the graph of the line as dotted line to indicate that the points on the line are not included from the solution sets.
If the inequality involves ‘≥’ or ‘≤’, we draw the graph of the line as a dark line to indicate the points on the line is included from the solution sets.
Solution of a linear inequality in one variable can be represented on number line as well as in the plane but the solution of a linear inequality in two variables of the type ax + by > c, ax + by ≥ c,ax + by < c or ax + by ≤ c (a ≠ 0, b ≠ 0) can be represented in the plane only.
Two or more inequalities taken together comprise a system of inequalities and the solution of the system of inequalities are the solution common to all the inequalities comprising the system.
Linear Inequalities Class 11 MCQs Questions with Answers
Question 1.
Sum of two rational numbers is ______ number.
(a) rational
(b) irrational
(c) Integer
(d) Both 1, 2 and 3
Answer
Answer: (a) rational
Hint:
The sum of two rational numbers is a rational number.
Ex: Let two rational numbers are 1/2 and 1/3
Now, 1/2 + 1/3 = 5/6 which is a rational number.
Question 2.
If x² = -4 then the value of x is
(a) (-2, 2)
(b) (-2, ∞)
(c) (2, ∞)
(d) No solution
Answer
Answer: (d) No solution
Hint:
Given, x² = -4
Since LHS ≥ 0 and RHS < 0
So, No solution is possible.
Question 3.
Solve: (x + 1)² + (x² + 3x + 2)² = 0
(a) x = -1, -2
(b) x = -1
(c) x = -2
(d) None of these
Answer
Answer: (b) x = -1
Hint:
Given, (x + 1)² + (x² + 3x + 2)² = 0
This is true when each term is equal to zero simultaneously,
So, (x + 1)² = 0 and (x² + 3x + 2)² = 0
⇒ x + 1 = 0 and x² + 3x + 2 = 0
⇒ x = -1, and x = -1, -2
Now, the common solution is x = -1
So, solution of the equation is x = -1
Question 4.
If (x + 3)/(x – 2) > 1/2 then x lies in the interval
(a) (-8, ∞)
(b) (8, ∞)
(c) (∞, -8)
(d) (∞, 8)
Answer
Answer: (a) (-8, ∞)
Hint:
Given,
(x + 3)/(x – 2) > 1/2
⇒ 2(x + 3) > x – 2
⇒ 2x + 6 > x – 2
⇒ 2x – x > -2 – 6
⇒ x > -8
⇒ x ∈ (-8, ∞)
Question 5.
The region of the XOY-plane represented by the inequalities x ≥ 6, y ≥ 2, 2x + y ≤ 10 is
(a) unbounded
(b) a polygon
(c) none of these
(d) exterior of a triangle
Answer
Answer: (c) none of these
Hint:
Given inequalities x ≥ 6, y ≥ 2, 2x + y ≤ 10
Now take x = 6, y = 2 and 2x + y = 10
when x = 0, y = 10
when y = 0, x = 5
So, the points are A(6, 2), B(0, 10) and C(5, 0)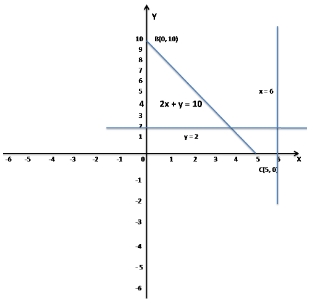
So, the region of the XOY-plane represented by the inequalities x ≥ 6, y ≥ 2, 2x + y ≤ 10 is not defined.
Question 6.
The interval in which f(x) = (x – 1) × (x – 2) × (x – 3) is negative is
(a) x > 2
(b) 2 < x and x < 1
(c) 2 < x < 1 and x < 3
(d) 2 < x < 3 and x < 1
Answer
Answer: (d) 2 < x < 3 and x < 1
Hint:
Given, f(x) = (x – 1) × (x – 2) × (x – 3) has all factors with odd powers.
So, put them zero
i.e. x – 1 = 0, x – 2 = 0, x – 3 = 0
⇒ x = 1, 2, 3
Now, f(x) < 0 when 2 < x < 3 and x < 1
Question 7.
If -2 < 2x – 1 < 2 then the value of x lies in the interval
(a) (1/2, 3/2)
(b) (-1/2, 3/2)
(c) (3/2, 1/2)
(d) (3/2, -1/2)
Answer
Answer: (b) (-1/2, 3/2)
Hint:
Given, -2 < 2x – 1 < 2
⇒ -2 + 1 < 2x < 2 + 1
⇒ -1 < 2x < 3
⇒ -1/2 < x < 3/2
⇒ x ∈(-1/2, 3/2)
Question 8.
The solution of the inequality |x – 1| < 2 is
(a) (1, ∞)
(b) (-1, 3)
(c) (1, -3)
(d) (∞, 1)
Answer
Answer: (b) (-1, 3)
Hint:
Given, |x – 1| < 2
⇒ -2 < x – 1 < 2
⇒ -2 + 1 < x < 2 + 1
⇒ -1 < x < 3
⇒ x ∈ (-1, 3)
Question 9.
If | x − 1| > 5, then
(a) x∈(−∞, −4)∪(6, ∞]
(b) x∈[6, ∞)
(c) x∈(6, ∞)
(d) x∈(−∞, −4)∪(6, ∞)
Answer
Answer: (d) x∈(−∞, −4)∪(6, ∞)
Hint:
Given |x−1| >5
Case 1:
(x – 1) > 5
⇒ x > 6
⇒ x ∈ (6,∞)
Case 2:
-(x – 1) > 5
⇒ -x + 1 > 5
⇒ -x > 4
⇒ x < -4
⇒ x ∈ (−∞, −4)
So the range of x is (−∞, −4)∪(6, ∞)
Question 10.
The solution of |2/(x – 4)| > 1 where x ≠ 4 is
(a) (2, 6)
(b) (2, 4) ∪ (4, 6)
(c) (2, 4) ∪ (4, ∞)
(d) (-∞, 4) ∪ (4, 6)
Answer
Answer: (b) (2, 4) ∪ (4, 6)
Hint:
Given, |2/(x – 4)| > 1
⇒ 2/|x – 4| > 1
⇒ 2 > |x – 4|
⇒ |x – 4| < 2
⇒ -2 < x – 4 < 2
⇒ -2 + 4 < x < 2 + 4
⇒ 2 < x < 6
⇒ x ∈ (2, 6) , where x ≠ 4
⇒ x ∈ (2, 4) ∪ (4, 6)
Question 11.
If (|x| – 1)/(|x| – 2) ≥ 0, x ∈ R, x ± 2 then the interval of x is
(a) (-∞, -2) ∪ [-1, 1]
(b) [-1, 1] ∪ (2, ∞)
(c) (-∞, -2) ∪ (2, ∞)
(d) (-∞, -2) ∪ [-1, 1] ∪ (2, ∞)
Answer
Answer: (d) (-∞, -2) ∪ [-1, 1] ∪ (2, ∞)
Hint:
Given, (|x| – 1)/(|x| – 2) ≥ 0
Let y = |x|
So, (y – 1)/(y – 2) ≥ 0
⇒ y ≤ 1 or y > 2
⇒ |x| ≤ 1 or |x| > 2
⇒ (-1 ≤ x ≤ 1) or (x < -2 or x > 2)
⇒ x ∈ [-1, 1] ∪ (-∞, -2) ∪ (2, ∞)
Hence the solution set is:
x ∈ (-∞, -2) ∪ [-1, 1] ∪ (2, ∞)
Question 12.
The solution of the -12 < (4 -3x)/(-5) < 2 is
(a) 56/3 < x < 14/3
(b) -56/3 < x < -14/3
(c) 56/3 < x < -14/3
(d) -56/3 < x < 14/3
Answer
Answer: (d) -56/3 < x < 14/3
Hint:
Given inequality is :
-12 < (4 -3x)/(-5) < 2
⇒ -2 < (4-3x)/5 < 12
⇒ -2 × 5 < 4 – 3x < 12 × 5
⇒ -10 < 4 – 3x < 60
⇒ -10 – 4 < -3x < 60-4
⇒ -14 < -3x < 56
⇒ -56 < 3x < 14
⇒ -56/3 < x < 14/3
Question 13.
If x² = -4 then the value of x is
(a) (-2, 2)
(b) (-2, ∞)
(c) (2, ∞)
(d) No solution
Answer
Answer: (d) No solution
Hint:
Given, x² = -4
Since LHS ≥ 0 and RHS < 0
So, No solution is possible.
Question 14.
Solve: |x – 3| < 5
(a) (2, 8)
(b) (-2, 8)
(c) (8, 2)
(d) (8, -2)
Answer
Answer: (b) (-2, 8)
Hint:
Given, |x – 3| < 5
⇒ -5 < (x – 3) < 5
⇒ -5 + 3 < x < 5 + 3
⇒ -2 < x < 8
⇒ x ∈ (-2, 8)
Question 15.
The graph of the inequations x ≥ 0, y ≥ 0, 3x + 4y ≤ 12 is
(a) none of these
(b) interior of a triangle including the points on the sides
(c) in the 2nd quadrant
(d) exterior of a triangle
Answer
Answer: (b) interior of a triangle including the points on the sides
Hint:
Given inequalities x ≥ 0, y ≥ 0, 3x + 4y ≤ 12
Now take x = 0, y = 0 and 3x + 4y = 12
when x = 0, y = 3
when y = 0, x = 4
So, the points are A(0, 0), B(0, 3) and C(4, 0)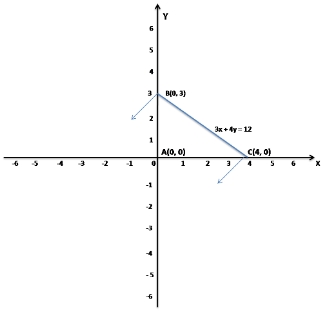
So, the graph of the inequations x ≥ 0, y ≥ 0, 3x + 4y ≤ 12 is interior of a triangle including the points on the sides.
Question 16.
If |x| < 5 then the value of x lies in the interval
(a) (-∞, -5)
(b) (∞, 5)
(c) (-5, ∞)
(d) (-5, 5)
Answer
Answer: (d) (-5, 5)
Hint:
Given, |x| < 5
It means that x is the number which is at distance less than 5 from 0
Hence, -5 < x < 5
⇒ x ∈ (-5, 5)
Question 17.
Solve: f(x) = {(x – 1)×(2 – x)}/(x – 3) ≥ 0
(a) (-∞, 1] ∪ (2, ∞)
(b) (-∞, 1] ∪ (2, 3)
(c) (-∞, 1] ∪ (3, ∞)
(d) None of these
Answer
Answer: (b) (-∞, 1] ∪ (2, 3)
Hint:
Given, f(x) = {(x – 1)×(2 – x)}/(x – 3) ≥ 0
or f(x) = -{(x – 1)×(2 – x)}/(x – 3)
which gives x – 3 ≠ 0
⇒ x ≠ 3![]()
Using number line rule as shown in the figure,
which gives f(x) ≥ 0 when x ≤ 1 or 2 ≤ x < 3
i.e. x ∈ (-∞, 1] ∪ (2, 3)
Question 18.
If x² = 4 then the value of x is
(a) -2
(b) 2
(c) -2, 2
(d) None of these
Answer
Answer: (c) -2, 2
Hint:
Given, x² = 4
⇒ x² – 4 = 0
⇒ (x – 2)×(x + 2) = 0
⇒ x = -2, 2
Question 19.
The solution of the 15 < 3(x – 2)/5 < 0 is
(a) 27 < x < 2
(b) 27 < x < -2
(c) -27 < x < 2
(d) -27 < x < -2
Answer
Answer: (a) 27 < x < 2
Hint:
Given inequality is:
15 < 3(x-2)/5 < 0
⇒ 15 × 5 < 3(x-2) < 0 × 5
⇒ 75 < 3(x-2) < 0
⇒ 75/3 < x-2 < 0
⇒ 25 < x-2 < 0
⇒ 25 +2 < x <0+2
⇒ 27 < x < 2
Question 20.
Solve: 1 ≤ |x – 1| ≤ 3
(a) [-2, 0]
(b) [2, 4]
(c) [-2, 0] ∪ [2, 4]
(d) None of these
Answer
Answer: (c) [-2, 0] ∪ [2, 4]
Hint:
Given, 1 ≤ |x – 1| ≤ 3
⇒ -3 ≤ (x – 1) ≤ -1 or 1 ≤ (x – 1) ≤ 3
i.e. the distance covered is between 1 unit to 3 units
⇒ -2 ≤ x ≤ 0 or 2 ≤ x ≤ 4
Hence, the solution set of the given inequality is
x ∈ [-2, 0] ∪ [2, 4]