CBSE Class 12 Mathematics Important Questions Chapter 1 Relations and Functions
1 Mark Questions
1. A Relation R:AàA is said to be Reflexive if ——— for every a  A where A is non
A where A is non
empty set.
Ans: (a, a)  R
R
2. A Relation R:AàA is said to be Symmetric if ———-  a,b,
a,b,  A
A
Ans: (a, b)  R, (b, a)
R, (b, a)  R
R
3. A Relation R:AàA is said to be Transitive if ————-  a,b,c
a,b,c  A
A
Ans: (a, b) R, and (b, c)
R, and (b, c) R
R  (a, c)
(a, c)  R.
R.
4. Define universal relation? Give example.
Ans: A Relation R in a set A called universal relation if each element of A is related to every element of A. Ex. Let = {2,3,4}
R = (A A) = {(2,2),(2,3) (2,4) (3,2) (3,3) (3,4) (4,2) (4,3) (4,4) }
A) = {(2,2),(2,3) (2,4) (3,2) (3,3) (3,4) (4,2) (4,3) (4,4) }
5. What is trivial relation?
Ans: Both the empty relation and the universal relation are some time called trivial relation.
6. Prove that the function f: R à R, given by f(x) = 2x, is one – one.
Ans: f is one – one as f(x1) = f (x1)
2x1 = 2x2
x1 = x2
Prove.
7. State whether the function is one – one, onto or bijective f: R à R defined by f(x) = 1+ x2
Ans: Let x1, x2  x
x
If f(x1) = f(x2)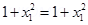
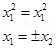
Hence not one – one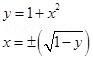
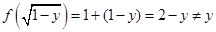
8. Let S = {1, 2, 3}
Determine whether the function f: S à S defined as below have inverse.
f = {(1, 2), (2, 1), (3, 1)}
Ans: f(2) = 1 f(3) = 1,
f is not one – one, So that that f is not invertible.
9. Find gof f(x) = |x|, g(x) = |5x + 1|
Ans: gof (x) = g [f(x)]
= g [(x)]
= 
10. Let f, g and h be function from R to R show that (f + g) oh = foh + goh
Ans: L.H.S = (f + g) oh
= {(f + g) oh} (x)
= (f + g) h (x)
= f [h (x)] + g [h (x)]
= foh + goh
9. If a * b = a + 3b2, then find 2 * 4
Ans: 2 * 4 = 2 + 3 (4)2
= 2 + 3  16
16
= 2 + 48
= 50
11. Show that function f: N à N, given by f(x) = 2x, is one – one.
Ans: the function f is one – one, for
f(x1) = f(x2)
2x1 = 2x2
x1 = x2
12. State whether the function is one – one, onto or bijective f: R à R defined by f(x) = 3 – 4x
Ans: is x1, x2  R
R
f(x1) = f(x2)
3 – 4x1 = 3 – 4x2
x1 = x2
Hence one – one
Y = 3 – 4x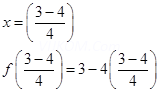
= y
Hence onto also.
13. Let S = {1, 2, 3}
Determine whether the function f: S à S defined as below have inverse.
f = {(1, 1), (2, 2), (3, 3)}
Ans: f is one – one and onto, so that f is invertible with inverse f-1 = {(1, 1) (2, 2) (3, 3)}
14. Find got f(x) = |x|, g(x) = |5x -2|
Ans: fog (x) = f(g x)
= f{|5x – 2|)
= |5x – 2|
15. Consider f: {1, 2, 3} à {a, b, c} given by f(1) = a, f(2) = b and f(3) = c find f-1 and show
that (f-1)-1 = f
Ans: f = {(1, a) (2, b) (3, c)}
f-1 = { (a, 1) (b, 2) (c, 3)}
(f -1) -1 = {(1, a) (2, b) (3, c)}
Hence (f-1)-1 = f.
16. If f(x) = x + 7 and g(x) = x – 7,  x
x  R find (fog) (7)
R find (fog) (7)
Ans: (fog) (x) = f[g(x)]
= f(x – 7)
= x – 7 + 7
= x
(fog) (7) = (7)
17. What is a bijective function?
Ans: A function f: X à Y is said to be one – one and onto (bijective), if f is both one – one and onto.
18 Let f: R à R be define as f(x) = x4 check whether the given function is one – one onto,
or other.
Ans: Let x1, x2  R
R
If f(x1) = f(x2)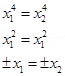
Not one – one
Not onto.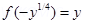
19 Let S = {1, 2, 3}
Determine whether the function f: S à S defined as below have inverse.
f = {(1, 3) (3, 2) (2, 1)}
Ans: f is one – one and onto, Ao that f is invertible with f-1 = {(3,1) (2, 3) (1, 2)}
20 Find gof where f(x) = 8x3, g(x) = x1/3
Ans: gof (x) = g[f(x)]
= g (8x3)
= 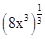
= 2x
21. Let f, g and h be function from R + R. Show that (f.g) oh = (foh). (goh)
Ans: (f. g) oh
(f. g) h (x)
f[h(x)]. g[h(x)]
foh. goh
21. Let * be a binary operation defined by a * b = 2a + b – 3. find 3 * 4
Ans: 3 * 4 = 2 (3) + 4-3 = 7
22. show that a one – one function f: {1, 2, 3} à {1, 2, 3} must be onto.
Ans: Since f is one – one three element of {1, 2, 3} must be taken to 3 different element of the co – domain {1, 2, 3} under f. hence f has to be onto.
23. f: R à R be defined as f(x) = 3x check whether the function is one – one onto or other
Ans: Let 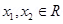
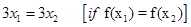
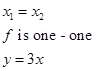
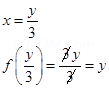
24. Let S = {1, 2, 3}
Determine whether the function f: S à S defined as below have inverse.
f = { (1, 2) (2, 1) (3, 1) }
Ans:f(2) = 1, f(3) =1
f is not one – one so that f is not invertible
Hence no inverse
25. Find fog f(x) = 8x3, g(x) = x1/3
Ans: fog (x) = f(gx)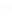

= 8x
26. If f: R à R be given by f(x) = 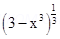 , find fof (x)
, find fof (x)
Ans: 

= 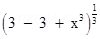
= x
27. If f(x) is an invertible function, find the inverse of f(x) = 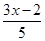
Ans: Let f(x) = y
4 Marks Questions
1. Let T be the set of all triangles in a plane with R a relation in T given by
R = {(T1, T2): T1 is congruent to T2}.
Show that R is an equivalence relation.
Ans. R is reflexive, since every  is congruent to itself.
is congruent to itself.
(T1T2) R similarly (T2T1)
R similarly (T2T1)  R
R since T1
since T1 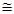 T2
T2
(T1T2)  R, and (T2,T3)
R, and (T2,T3)  R
R (T1T3)
(T1T3) R Since three triangles are
R Since three triangles are
congruent to each other.
2. Show that the relation R in the set Z of integers given byR={(a, b) : 2 divides a-b}. is equivalence relation.
Ans. R is reflexive , as 2 divide a-a = 0
((a,b) R ,(a-b) is divide by 2
R ,(a-b) is divide by 2 (b-a) is divide by 2 Hence (b,a)
(b-a) is divide by 2 Hence (b,a)  R hence symmetric.
R hence symmetric.
Let a,b,c  Z
Z
If (a,b)  R
R
And (b,c)  R
R
Then a-b and b-c is divided by 2 a-b +b-c is even
a-b +b-c is even (a-c is even
(a-c is even (a,c)
(a,c)  R
R
Hence it is transitive.
3. Let L be the set of all lines in plane and R be the relation in L define if R = {(l1, L2 ): L1 is 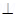 to L2 } . Show that R is symmetric but neither reflexive nor transitive.
to L2 } . Show that R is symmetric but neither reflexive nor transitive.
Ans. R is not reflexive , as a line L1 cannot be 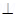 to itself i.e (L1,L1 )
to itself i.e (L1,L1 ) 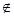 R
R L1
L1 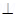 L2
L2 L2
L2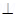 L1
L1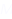
 (L2,L1)
(L2,L1) R
R
L1 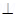 L2 and L2
L2 and L2 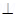 L3
L3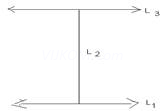
Then L1 can never be 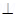 to L3 in fact L1 || L3
to L3 in fact L1 || L3
i.e (L1,L2)  R, (L2,L3)
R, (L2,L3)  R.
R.
But (L1, L3)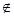 R
R
4. Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} asR = {(a, b): b = a+1} is reflexive, symmetric or transitive.
Ans. R = {(a,b): b= a+1}
Symmetric or transitive
R = {(1,2) (2,3) (3,4) (4,5) (5,6) }
R is not reflective , because (1,1) 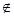 R
R
R is not symmetric because (1,2) R but (2,1)
R but (2,1) 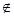 R
R
(1,2)  R and (2,3)
R and (2,3)  R
R
But (1,3) 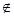 R Hence it is not transitive
R Hence it is not transitive
5. Let L be the set of all lines in xy plane and R be the relation in L define as R = {(L1, L2): L1 || L2} Show then R is on equivalence relation.
Find the set of all lines related to the line y=2x+4.
Ans. L1||L1 i.e (L1, L1)  R Hence reflexive
R Hence reflexive
L1||L2 then L2 ||L1 i.e (L1L2) R
R (L2,L)
(L2,L) R Hence symmetric
R Hence symmetric
We know the
L1||L2 and L2||L3
Then L1|| L3
Hence Transitive . y = 2x+K
When K is real number.
6. Show that the relation in the set R of real no. defined R = {(a, b) : a 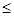 b3 }, is neither reflexive nor symmetric nor transitive.
b3 }, is neither reflexive nor symmetric nor transitive.
Ans. (i) (a, a) 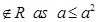 Which is false R is not reflexive.
Which is false R is not reflexive.
(ii) 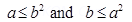 Which is false R is not symmetric.
Which is false R is not symmetric.
(iii) 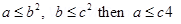 Which is false
Which is false
7. Let A = N  N and * be the binary operation on A define by (a, b) * (c, d) = (a + c, b + d)Show that * is commutative and associative.
N and * be the binary operation on A define by (a, b) * (c, d) = (a + c, b + d)Show that * is commutative and associative.
Ans. (i) (a, b) * (c, d) = (a + c, b + d)
= (c + a, d + b)
= (c, d) * (a, b)
Hence commutative
(ii) (a, b) * (c, d) * (e, f)
= (a + c, b + d) * (e, f)
= (a + c + e, b + d + f)
= (a, b) * (c + e, d + f)
= (a, b) * (c, d) * (e, f)
Hence associative.
8. Show that if f: 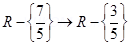 is defining by f(x) =
is defining by f(x) = 
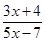 and g:
and g: 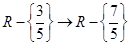 is define by
is define by
g(x) = 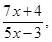 then fog = IA and gof = IB when
then fog = IA and gof = IB when 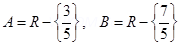 ; IA (x) = x, for all x
; IA (x) = x, for all x  A, IB(x) = x, for all x
A, IB(x) = x, for all x  B are called identify function on set A and B respectively.
B are called identify function on set A and B respectively.
Ans. gof (x) = 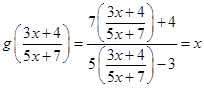
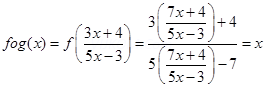

Which implies that gof = IB
And Fog = IA
9. Let f: N à N be defined by f(x) = 
Examine whether the function f is onto, one – one or bijective
Ans. 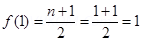

f is not one – one
1 has two pre images 1 and 2
Hence f is onto
f is not one – one but onto.
10. Show that the relation R in the set of all books in a library of a collage given by R ={(x, y) : x and y have same no of pages}, is an equivalence relation.
Ans. (i) (x, x)  R, as x and x have the same no of pages for all x
R, as x and x have the same no of pages for all x R
R  R is reflexive.
R is reflexive.
(ii) (x, y) R
x and y have the same no. of pages
y and x have the same no. of pages (y, x)
(y, x)  R
R (x, y) = (y, x) R is symmetric.
(x, y) = (y, x) R is symmetric.
(iii) if (x, y)  R, (y, y)
R, (y, y)  R
R
(x, z)  R
R R is transitive.
R is transitive.
11. Let * be a binary operation. Given by a * b = a – b + abIs * :
(a) Commutative
(B) Associative
Ans. (i) a * b = a – b + ab
b * a = b – a + ab
a * b  b * a
b * a
(ii) a * (b * c) = a * (b – c + bc)
= a – (b – c + bc) + a. (b – c + bc)
= a – b + c – bc + ab – ac + abc
(a * b) * c = (a – b + ab) * c
= [ (a – b + ab) – c ] + ( a – b + ab)
= a- b + ab – c + ac – bc + abc
a * (b * c)  (a * b) * c.
(a * b) * c.
12. Let f: R à R be f (x) = 2x + 1 and g: R à R be g(x) = x2 – 2 find (i) gof (ii) fog
Ans. (i) gof (x) = g[f(x)]
= g (2x + 1)
= (2x + 1)2 – 2
(ii) fog (x) = f (fx)
= f (2x + 1)
= 2(2x + 1) + 1
= 4x + 2 + 1 = 4x + 3
13. Let A = R – {3} and B = R- {1}. Consider the function of f: A à B defined by
f(x) =  is f one – one and onto.
is f one – one and onto.
Ans. Let x1 x2  A
A
Such that f(x1) = f(x2)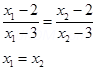
f is one – one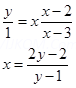

Hence onto
14. Show that the relation R defined in the set A of all triangles asR = {  is similar to T2 }, is an equivalence relation. Consider three right angle triangles T1 with sides 3, 4, 5. T2 with
is similar to T2 }, is an equivalence relation. Consider three right angle triangles T1 with sides 3, 4, 5. T2 with
sides 5, 12, 13 and T3 with sides 6, 8, 10. Which triangles among T1, T2 and T3 are related?
Ans. (i) Each triangle is similar to at well and thus (T1, T1)  R
R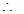 R is reflexive.
R is reflexive.
(ii) (T1, T2)  R
R T1 is similar to T2
T1 is similar to T2 T2 is similar to T1
T2 is similar to T1
(T2, T1)  R
R
R is symmetric
(iii) T1 is similar to T2 and T2 is similar to T3 T1 is similar to T3
T1 is similar to T3 (T1, T3)
(T1, T3)  R
R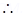 R is transitive.
R is transitive.
Hence R is equivalence
(II) part T1 = 3, 4, 5
T2 = 5, 12, 13
T3 = 6, 8, 10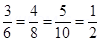 T1 is relative to T3.
T1 is relative to T3.
15. Determine which of the following operation on the set N are associative and which are commutative.
(a) a * b = 1 for all a, b  N
N
(B) a * b = 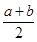 for all a, b,
for all a, b,  N
N
Ans. (a) a * b = 1
b * a = 1
for all a, b  N also
N also
(a * b) * c = 1 * c = 1
a * (b * c) = a * (1) = 1 for all, a, b, c R N
Hence R is both associative and commutative
(b) a * b = 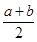 , b * a =
, b * a = 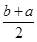
Hence commutative.
(a * b) * c = 
=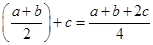
= 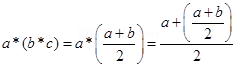
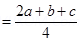
* is not associative.
17. Let A and B be two sets. Show that f: A  B à B
B à B  A such that f(a, b) = (b, a) is a bijective function.
A such that f(a, b) = (b, a) is a bijective function.
Ans. Let (a1 b1) and (a2, b2)  A
A  B
B
(i) f(a1 b1) = f(a2, b2)
b1 = b2 and a1 = a2
(a1 b1) = (a2, b2)
Then f(a1 b1) = f(a2, b2)
(a1 b1) = (a2, b2) for all
(a1 b1) = (a2, b2)  A
A  B
B
(ii) f is injective,
Let (b, a) be an arbitrary
Element of B  A. then b
A. then b  B and a
B and a  A
A (a, b) )
(a, b) )  (A
(A  B)
B)
Thus for all (b, a)  B
B  A their exists (a, b) )
A their exists (a, b) )  (A
(A  B)
B)
Hence that
f(a, b) = (b, a)
So f: A  B à B
B à B  A
A
Is an onto function.
Hence bijective
18. Show that the relation R defined by (a, b) R (c, d)  a + b = b + c on the set N
a + b = b + c on the set N  N is an equivalence relation.
N is an equivalence relation.
Ans. (a, b) R (c, d)  a + b = b + c where a, b, c, d
a + b = b + c where a, b, c, d  N
N
(a, b ) R (a, b)  a + b = b + a (a, b)
a + b = b + a (a, b)  N
N  N
N
R is reflexive
(a, b) R (c, d)  a + b
a + b
= b + c (a, b ) (c, d)  N
N  N
N d + a = c + b
d + a = c + b c + b = d + a
c + b = d + a (c, d) R (a, b) (a, b), (c, d)
(c, d) R (a, b) (a, b), (c, d)  N
N  N
N
Hence reflexive.
(a, b) R (c, d)  a + d = b + c (1) (a, b), (c, d)
a + d = b + c (1) (a, b), (c, d)  N
N  N
N
(c, d) R (e, f)  c + f = d + e (2) (c, d), (e, f)
c + f = d + e (2) (c, d), (e, f)  N
N  N
N
Adding (1) and (2)
(a + b) + [(+f)] = (b + c) + (d + e)
a + f = b + e
(a, b) R (e, f)
Hence transitive
So equivalence
19. Let * be the binary operation on H given by a * b = L. C. M of a and b. find
(a) 20 * 16
(b) Is * commutative
(c) Is * associative
(d) Find the identity of * in N.
Ans. (i) 20 * 16 = L. C.M of 20 and 16
= 80 
(ii) a * b = L.C.M of a and b
= L.C.M of b and a
= b * a
(iii) a * (b * c) = a * (L.C.M of b and c)
= L.C.M of (a and L.C.M of b and c)
= L.C.M of a, b and c
Similarity
(a * b) * c = L. C.M of a, b, and c
(iv) a * 1 = L.C.M of a and 1= a
=1
20. If the function f: R à R is given by f(x) =  and g: R à R is given by g(x) = 2x – 3, Find
and g: R à R is given by g(x) = 2x – 3, Find
(i) fog
(ii) gof. Is f-1 = g
(iii) fog = gof = x
Ans. (i) fog (x) = f [g(x)]
= f (2x – 3)
= 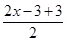
= x
(ii) gof (x) = g [f(x)]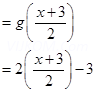
= x
(iii) fog = gof = x
Yes,
21. Let L be the set of all lines in Xy plane and R be the relation in L define as R = {(L1, L2): L1 || L2} Show then R is on equivalence relation.
Find the set of all lines related to the line y=2x+4.
Ans. L1||L1 i.e (L1, L1)  R Hence reflexive
R Hence reflexive
L1||L2 then L2 ||L1 i.e (L1L2) R
R (L2, L)
(L2, L) R Hence symmetric
R Hence symmetric
We know the
L1||L2 and L2||L3
Then L1|| L3
Hence Transitive. y = 2x+K
When K is real no.
Relations and Functions Class 12 Maths MCQs
1. Let R be a relation on the set L of lines defined by l1 R l2 if l1 is perpendicular to l2, then relation R is
(a) reflexive and symmetric
(b) symmetric and transitive
(c) equivalence relation
(d) symmetric
Answer/Explanation
Answer: d
Explaination: (d), not reflexive, as l1 R l2
⇒ l1 ⊥ l1 Not true
Symmetric, true as l1 R l2 ⇒ l2R h
Transitive, false as l1 R l2, l2 R l3
⇒ l1 || l3 . l1 R l2.
2. Given triangles with sides T1 : 3, 4, 5; T2 : 5, 12, 13; T3 : 6, 8, 10; T4 : 4, 7, 9 and a relation R in set of triangles defined as R = {(Δ1, Δ2) : Δ1 is similar to Δ2}. Which triangles belong to the same equivalence class?
(a) T1 and T2
(b) T2 and T3
(c) T1 and T3
(d) T1 and T4
Answer/Explanation
Answer: c
Explaination: (c), T1 and T3 are similar as their sides are proportional.
3. Given set A ={1, 2, 3} and a relation R = {(1, 2), (2, 1)}, the relation R will be
(a) reflexive if (1, 1) is added
(b) symmetric if (2, 3) is added
(c) transitive if (1, 1) is added
(d) symmetric if (3, 2) is added
Answer/Explanation
Answer: c
Explaination: (c), here (1,2) e R, (2,1) € R, if transitive (1,1) should belong to R.
4. Given set A = {a, b, c). An identity relation in set A is
(a) R = {(a, b), (a, c)}
(b) R = {(a, a), (b, b), (c, c)}
(c) R = {(a, a), (b, b), (c, c), (a, c)}
(d) R= {(c, a), (b, a), (a, a)}
Answer/Explanation
Answer: b
Explaination: (b), A relation R is an identity relation in set A if for all a ∈ A, (a, a) ∈ R.
5. A relation S in the set of real numbers is defined as xSy ⇒ x – y+ √3 is an irrational number, then relation S is
(a) reflexive
(b) reflexive and symmetric
(c) transitive
(d) symmetric and transitive
Answer/Explanation
Answer: a
Explaination:
6. Set A has 3 elements and the set B has 4 elements. Then the number of injective functions that can be defined from set A to set B is
(a) 144
(b) 12
(c) 24
(d) 64
Answer/Explanation
Answer: c
Explaination: (c), total injective mappings/functions
= 4 P3 = 4! = 24.
7. Given a function lf as f(x) = 5x + 4, x ∈ R. If g : R → R is inverse of function ‘f then
(a) g(x) = 4x + 5
(b) g(x) = \(\frac{5}{4 x-5}\)
(c) g(x) = \(\frac{x-4}{5}\)
(d) g(x) = 5x – 4
Answer/Explanation
Answer: c
Explaination: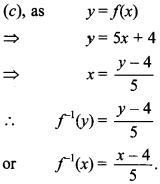
8. Let Z be the set of integers and R be a relation defined in Z such that aRb if (a – b) is divisible by 5. Then R partitions the set Z into ______ pairwise disjoint subsets.
Answer/Explanation
Answer:
Explaination: Five, as remainder can be 0, 1, 2, 3, 4.
9. Consider set A = {1, 2, 3 } and the relation R= {(1, 2)}, then? is a transitive relation. State true or false.
Answer/Explanation
Answer:
Explaination: True, as there is no situation
(a, b) ∈ R, (b, c) ∈ R Hence, transitive. We can also say, a relation containing only one element is transitive.
10. Every relation which is symmetric and transitive is reflexive also. State true or false.
Answer/Explanation
Answer:
Explaination: False,e.g.if R is arelationinset A = {2,3,4} defined as {(2, 3), (3, 2), (2, 2)} is symmetric and transitive but not reflexive.
11. Let R be a relation in set N, given by R = {(a, b): a = b – 2, b > 6} then (3, 8) ∈ R. State true or false with reason.
Answer/Explanation
Answer:
Explaination: False, as in (3, 8), b = 8
⇒ a = 8 – 2
⇒ a = 6, but here a = 3.
12. Let R be a relation defined as R = {(x, x), (y, y), (z, z), (x, z)} in set A = {x, y, z} then R is (reflexive/symmetric) relation.
Answer/Explanation
Answer:
Explaination: Reflexive, as for all a ∈ A, (a, a) ∈ R.
13. Let R be a relation in the set of natural numbers N defined by R = {(a, b) ∈ N × N: a < b}. Is relation R reflexive? Give a reason.
Answer/Explanation
Answer:
Explaination:
Given R = {(a, b) ∈ N × N: a < b}.
Not reflexive, as for (a, a) × R
⇒ a< a, not true.
14. Let A be any non-empty set and P(A) be the power set of A. A relation R defined on P(A) by X R Y ⇔ X ∩ Y = X, X, Y ∈ P(A). Examine whether ? is symmetric.
Answer/Explanation
Answer:
Explaination: X R Y ⇔ X ∩ Y = X ⇒ Y ∩ X = X ⇒ Y R X.
Hence, symmetric.
15. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive. [NCERT; Delhi 2011]
Answer/Explanation
Answer:
Explaination: (1, 2) ∈ R, (2, 1) ∈ R, but (1, 1) ∉ R.
16. Show that the relation R in the set {1,2,3} given by R = {(1,1), (2, 2), (3, 3), (1, 2), (2, 3)} is reflexive but neither symmetric nor transitive. [NGERT]
Answer/Explanation
Answer:
Explaination:
Given R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} defined on R: {1, 2, 3} → {1, 2, 3}
For reflexive: As (1, 1), (2,2), (3, 3) ∈ R. Hence, reflexive
For symmetric: (1, 2) ∈ R but (2, 1) ∉ R. Hence, not symmetric.
For transitive: (1, 2) ∈ R and (2, 3) ∈R but (1, 3) ∉ R. Hence, not transitive.
17. Let A = {3, 4, 5} and relation R on set A is defined as R = {(a, b) e A x A : a – b – 10). Is relation an empty relation?
Answer/Explanation
Answer:
Explaination: We notice for no value of a, b s A, a-b = 10. Hence, (a, b) £ R for a, b e A. Hence, empty relation.
18. Given set A = {a, b} and relation R on A is defined as R = {(a, a), (b, b)}. Is relation an identity relation?
Answer/Explanation
Answer:
Explaination: Yes, as (a, a) ∈ R, for all a ∈ A..
19. Let set A represents the set of all the girls of a particular class. Relation R on A is defined as R = {(a, b) ∈ A × A : difference between weights of a and b is less than 30 kg}. Show that relation R is a universal relation.
Answer/Explanation
Answer:
Explaination: Let a, b ∈ A then a – b < 30 kg, always true for students of a particular class, i.e. aRb ∀ a, b ∈ A. Hence, universal relation.
20. If A = {1, 2, 3} and relation R = {(2, 3)} in A. Check whether relation R is reflexive, symmetric and transitive.
Answer/Explanation
Answer:
Explaination:
Not reflexive, as (1, 1) ∉ R.
Not symmetric, as (2, 3) ∈ R but (3,2) ∉ R.
Transitive, as relation R in a non empty set containing one element is transitive.
21. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive. [Delhi]
Answer/Explanation
Answer:
Explaination: As (1, 2) ∈ R, (2, 1) ∈ R, but (1, 1) ∉ R.
22. Consider the set A containing n elements, then the total number of injective functions from set A onto itself is _____ .
Answer/Explanation
Answer:
Explaination: Total number of injective functions from set containing n elements to a set containing n elements is n Pn = n!
23. The domain of the function f : R → R defined by f(x) = \(\sqrt{4-x^{2}}\) is ______ .
Answer/Explanation
Answer:
Explaination:
[-2, 2]. For domain 4 – x² ≥ 0
⇒ 4 ≥ x²
⇒ x² ≤ 4
⇒ x² ≤ (2)²
⇒ -2 ≤ x ≤ 2, i.e. [-2, 2].
24. Let A = {a, b }. Then number of one-one functions from A to A possible are
(a) 2
(b) 4
(c) 1
(d) 3
Answer/Explanation
Answer:
Explaination: (a), as if n(A) = m, then possible one-one functions from A to A are m!
25. Let A = {1, 2, 3, 4} and B = {a, b, c}. Then number of one-one functions from A to B are ______.
Answer/Explanation
Answer:
Explaination: 0, as n(A) > n(B)
26. If n(A) = p, then number of bijective functions from set A to A are ______ ..
Answer/Explanation
Answer:
Explaination: p!, as for bijective functions from A to B, n(A) = n(B) and function is one-one onto.
27. The function f : R → R defined as f(x) = [x], where [x] is greatest integer ≤ x, is onto function. State true or false.
Answer/Explanation
Answer:
Explaination: False, as range of f is set of integers, i.e.
Z and range of f ⊆ co-domain R. Hence,not onto e.g. for \(\frac{1}{2}\) ∈ R (co-domain) there is no x ∈ R (domain) such that y = f(x) or \(\frac{1}{2}\) e∈ R has no pre-image.
28. If \(f(x)=\frac{x-1}{|x-1|}, x(\neq 1) \in R\) then range of ‘f’ is _______ .
Answer/Explanation
Answer:
Explaination:![]()
29. If f : R → R be defined by f(x) = (3 – x3)1/3, then find fof(x). [NCERT]
Answer/Explanation
Answer:
Explaination:![]()
30. If f is an invertible function defined as f(x) = \(\frac{3x-4}{5}\), write f-1(x).
Answer/Explanation
Answer:
Explaination: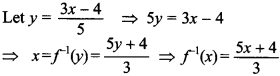
31. Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. State whether f is one-one or not. [AI 2011] f
Answer/Explanation
Answer:
Explaination: One-one, as for x1 ≠ x2
⇒ f(x1) ≠ f(x2).
32. Let f : R → R is defined by f (x) = | x |. Is function f onto? Give a reason. [HOTS]
Answer/Explanation
Answer:
Explaination: f is not onto, as for some y ∈ R from co-domain, there is no x ∈ R from domain such that y = f(x), e.g. for -2 ∈ R (co-domain) there is no x ∈ R (domain) such that f(x) = -2, i.e. |x| = -2. Hence, not onto.
33. If f : R → R and g : R → R are given by f (x) = sin x and g(x) = 5x², find gof(x).
Answer/Explanation
Answer:
Explaination: gof(x) = g(f(x)) = g(sin x) = 5 sin² x.
34. Let f : {1, 3,4} → {1,2, 5} and g: {1,2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof. [NCERT]
Answer/Explanation
Answer:
Explaination:
gof: {1, 3, 4} → {1, 3}.
gof(1) = g(f(1)) = g(2) = 3.
gof(3) = g(K3)) = g(5) = 1
gof(4) = g(f(4)) = g(1) = 3
gof = {(1, 3), (3, 1), (4, 3)}.
35. Prove that f : R → R given by f(x) = x3 + 1 is one-one function.
Answer/Explanation
Answer:
Explaination:
Given f(x) = x3 + 1
For x1 ≠ x2
⇒ x13 ≠ x23
⇒ x13 + 1 ≠ x23 + 1
⇒ f(x1) ≠ f(x2). Hence, one-one
36. Show that the Signum Function f : R → R,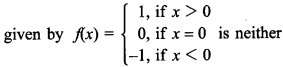
one-one nor onto.
Answer/Explanation
Answer:
Explaination: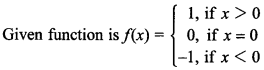
Range of function is {-1, 0, 1} and co-domain is set of real numbers R.
⇒ Range ⊆ co-domain.
There is at least one element in R(codomain) which is not image of any element of the domain, e.g. for 2 e R(co-domain), there is no x in domain such that f(x) = 2, x ∈ R.
Hence, function is not onto.
Also, let x1 = 2 and x2 = 3 then f(x1) = 1 and f(x2) = 1
i.e., x1 ≠ x2 ⇒ f(x1) = f(x2).
So, function is not one-one.
37. Given f(x) = sin x check if function f is one-one for (i) (0, π) (ii) (-\(\frac{π}{2}\), \(\frac{π}{2}\)).
Answer/Explanation
Answer:
Explaination: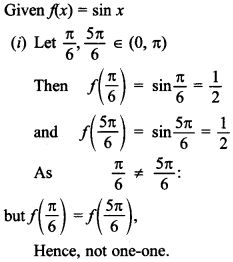
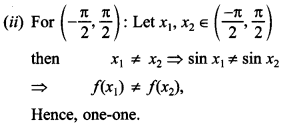
38. If f : R → R is defined by f(x) = 3x + 2, define f (f(x)). [Foreign]
Answer/Explanation
Answer:
Explaination: f(f(x)) = f(3x + 2) = 3(3x + 2) + 2
= 9x+ 8.
39. Write fog, if f : R → R and g : R → R are given by f(x) = |x| and g(x) = |5x – 2|. [Foreign]
Answer/Explanation
Answer:
Explaination: (fog)(x) =f(g(x))
=f(|5x-2|) = ||5x-2||.
40. Write fog, if f : R → R and g : R → R are given by f(x) = 8x3 and g(x) = x1/3. [Foreign]
Answer/Explanation
Answer:
Explaination: (fog)(x) = f(g(x)) = f(x1/3) = 8(x1/3)3 = 8x.