Question
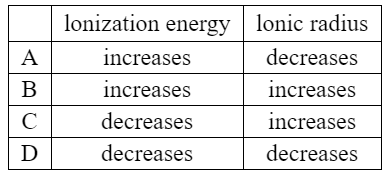
Discuss: How do the following properties change down Group 17 of the periodic table?
▶️Answer/Explanation
Ans:C
Solution:
The ionization energy decreases down Group 17, as the atomic radius increases and the valence electrons are further from the nucleus. This makes it easier to remove an electron from the outermost shell, and therefore the ionization energy decreases.
The ionic radius increases down Group 17, as the number of electron shells increases and the valence electrons are further from the nucleus. This makes the atoms larger and the ionic radius increases.
Therefore, the correct option is C: decreases for ionization energy and increases for ionic radius.
Question
What can be deduced from the period number of an element?
I. Highest occupied energy level
II. Number of sub-levels in the outer shell
III. Number of outer electrons
A. I and II only
B. I and III only
C. II and III only
D. I, II and III
▶️Answer/Explanation
Markscheme: A
The period number of an element corresponds to the highest occupied energy level (shell) of its electrons. Therefore, from the period number, you can deduce:
I. Highest occupied energy level – Yes, this is correct.
II. Number of sub-levels in the outer shell – The period number alone does not provide information about the number of sub-levels in the outer shell. This information is related to the specific electron configuration of the element.
III. Number of outer electrons – The period number can give you a rough idea of the number of outer electrons. For elements in a given period, the outer electrons are found in the same principal energy level. However, the specific number of outer electrons depends on the element’s position within the period.
Therefore, the correct answer is A. I and II only.
Question
Given: The energy from burning $0.250 \mathrm{~g}$ of ethanol causes the temperature of $150 \mathrm{~cm}^3$ of water to rise by $10.5^{\circ} \mathrm{C}$. Specific heat capacity of water: $4.18 \mathrm{~J} \mathrm{~g}^{-1} \mathrm{~K}^{-1}$.
Discuss: What is the enthalpy of combustion of ethanol, in $\mathrm{kJ} \mathrm{mol}^{-1}$ ?
A. $\frac{150 \times 4.18 \times 10.5}{\frac{0.250}{46.08}}$
B. $\frac{150 \times 4.18 \times 10.5}{\frac{0.250}{46.08} \times 1000}$
C. $\frac{150 \times 4.18 \times(273+10.5)}{\frac{0.250}{46.08}}$
D. $\frac{150 \times 4.18 \times(273+10.5)}{\frac{0.250}{46.08} \times 1000}$
▶️Answer/Explanation
Solution:
The enthalpy of combustion of ethanol, $\Delta H_{comb}$, can be calculated using the equation:
$$\Delta H_{comb} = -\frac{q}{n}$$
where $q$ is the energy released by burning $0.250 \mathrm{~g}$ of ethanol, $n$ is the number of moles of ethanol burned, and the negative sign is because the combustion of ethanol is an exothermic reaction.
The energy released by burning $0.250 \mathrm{~g}$ of ethanol can be calculated using the formula:
$$q = mc\Delta T$$
where $m$ is the mass of water, $c$ is the specific heat capacity of water, and $\Delta T$ is the change in temperature of water.
Substituting the given values, we get:
$$q = (150 \mathrm{~g}) (4.18 \mathrm{~J} \mathrm{~g}^{-1} \mathrm{~K}^{-1}) (10.5^\circ \mathrm{C})$$
To calculate the number of moles of ethanol burned, we need to use the molar mass of ethanol, which is $46.08 \mathrm{gmol}^{-1}$. The number of moles of ethanol burned is therefore:
$$n = \frac{0.250 \mathrm{~g}}{46.08 \mathrm{gmol}^{-1}}$$
Substituting these values into the equation for $\Delta H_{comb}$, we get:
$$\Delta H_{comb} = -\frac{q}{n} = -\frac{ (150 \mathrm{~g}) (4.18 \mathrm{~J} \mathrm{~g}^{-1} \mathrm{~K}^{-1}) (10.5^\circ \mathrm{C})}{ \frac{0.250 \mathrm{~g}}{46.08 \mathrm{gmol}^{-1}}}$$
To convert this to kilojoules per mole, we divide by 1000:
$$\colorbox{yellow}{$\Delta H_{comb} =\frac{150 \times 4.18 \times 10.5}{\frac{0.250}{46.08} \times 1000}$ Correct Option : B}$$
Question
Calculate :molar mass of a gas according to the following experimental data?
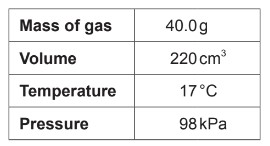
Ideal gas constant = 8.31 \(JK^{-1} mol^{-1}\)
A. \(\frac{40.0 \times 8.31 \times 290}{98 \times 0.220}\)
B. \(\frac{98 \times 0.220}{40.0 \times 8.31 \times 290}\)
C. \(\frac{40.0 \times 8.31 \times 17}{98 \times 0.220}\)
D. \(\frac{98 \times 220}{40.0 \times 8.31 \times 17}\)
▶️Answer/Explanation
Markscheme: A
To find the molar mass of the gas, you can rearrange the ideal gas law equation \(\mathrm{PV}=\mathrm{nRT}\) to solve for the number of moles (\(\mathrm{n}\)) and then use the formula for molar mass (\(\mathrm{M}\)):
\[\mathrm{Molar\ mass} (\mathrm{M}) = \frac{\text{Mass of gas}}{\text{Number of moles}}\]
First, find the number of moles using the ideal gas law:
\[\mathrm{n} = \frac{\mathrm{PV}}{\mathrm{RT}}\]
Now, substitute the given values:
\[\mathrm{n} = \frac{(98 \, \mathrm{kPa}) \times (0.220 \, \mathrm{L})}{(8.31 \, \mathrm{J} \, \mathrm{K}^{-1} \, \mathrm{mol}^{-1}) \times (290 \, \mathrm{K})}\]
Now, substitute the value of \(\mathrm{n}\) into the formula for molar mass:
\[\mathrm{M} = \frac{\text{Mass of gas}}{\text{Number of moles}} = \frac{40.0 \, \mathrm{g}}{\mathrm{n}}\]
so, \[\mathrm{M} =\frac{40.0 \times 8.31 \times 290}{98 \times 0.220}\]