Question
A particle moves in a straight line, starting from rest at a point O, and comes to instantaneous rest at a point P. The velocity of the particle at time ts after leaving O is v \(ms^{-2}\) , where \(\upsilon =0.6t^{2}-0.12t^{3}\)
(i) Show that the distance OP is 6.25 m. On another occasion, the particle also moves in the same straight line. On this occasion, the
displacement of the particle at time ts after leaving O is s m, where s=\(kt^{3}+ct^{5}\) It is given that the particle passes point P with velocity 1.25 \(m s^{-1}\) at time t = 5.
(ii) Find the values of the constants k and c.
(iii) Find the acceleration of the particle at time t = 5.
▶️Answer/Explanation
(i) To find the distance OP, we need to integrate the velocity function over the given time interval. The velocity function is given by \(v = 0.6t^2 – 0.12t^3\).
The distance traveled (\(s\)) is given by the integral of the velocity function with respect to time (\(t\)) from the initial time (\(t = 0\)) to the final time (\(t = t_s\)):
\(s = \int_{0}^{t_s} v \,dt\)
\(s = \int_{0}^{t_s} (0.6t^2 – 0.12t^3) \,dt\)
To find \(t_s\), we set \(v = 0\):
\(0.6t^2 – 0.12t^3 = 0\)
\(0.6t^2(1 – 0.2t) = 0\)
So, \(t = 0\) or \(t = 5\). Since the particle starts from rest at \(t = 0\), \(t_s = 5\).
Now, we evaluate the integral:
\(s = \int_{0}^{5} (0.6t^2 – 0.12t^3) \,dt\)
\(s = \left[0.2t^3 – 0.03t^4\right]_{0}^{5}\)
\(s = (0.2(5)^3 – 0.03(5)^4) – (0.2(0)^3 – 0.03(0)^4)\)
\(s = 6.25 \,m\)
Therefore, the distance \(OP\) is \(6.25 \,m\).
(ii) Now, the displacement function is given by \(s = kt^3 + ct^5\). We know that the particle passes point \(P\) with a velocity of \(1.25 \,m/s\) at \(t = 5\).
First, we find the velocity at \(t = 5\) by taking the derivative of the displacement function:
\(v = \frac{ds}{dt} = 3kt^2 + 5ct^4\)
At \(t = 5\), \(v = 1.25 \,m/s\):
\(1.25 = 3k(5)^2 + 5c(5)^4\)
\(1.25 = 75k + 3125c\)
Now, we are given that the particle is at point \(P\) at \(t = 5\), so \(s(5) = 6.25\):
\(s = kt^3 + ct^5\)
\(6.25 = k(5)^3 + c(5)^5\)
\(6.25 = 125k + 3125c\)
Now, we have a system of two equations:
\(75k + 3125c = 1.25\)
\(125k + 3125c = 6.25\)
Solving these equations simultaneously will give us the values of \(k\) and \(c\).
The given system of equations is:
\( \begin{align*}
& k \times 5^3+c \times 5^5=6.25 \\
& 125k+3125c=6.25 \\
& 75k+3125c=1.25 \\
\end{align*} \)
Solving these equations simultaneously:
From the first equation, we have:
\(125k + 3125c = 6.25\)
From the third equation, we have:
\(75k + 3125c = 1.25\)
Subtracting the third equation from the first equation:
\((125k + 3125c) – (75k + 3125c) = 6.25 – 1.25\)
\(50k = 5\)
\(k = 0.1\)
Substitute \(k = 0.1\) into the third equation:
\(75(0.1) + 3125c = 1.25\)
\(7.5 + 3125c = 1.25\)
\(3125c = -6.25\)
\(c = -0.002\)
Therefore, the values of \(k\) and \(c\) are \(k = 0.1\) and \(c = -0.002\).
(iii) The given acceleration function is:
\(\mathrm{a} = 0.6t – 0.04t^3\)
At \(t = 5\):
\(\mathrm{a} = 0.6(5) – 0.04(5)^3\)
\(\mathrm{a} = 3 – 0.04(125)\)
\(\mathrm{a} = 3 – 5\)
\(\mathrm{a} = -2 \,m/s^2\)
Therefore, the acceleration of the particle at \(t = 5\) is \(-2 \,m/s^2\).
Question
A particle P is projected vertically upwards with speed 24 m\( s^{−1}\) from a point 5 m above ground level. Find the time from projection until P reaches the ground.
▶️Answer/Explanation
\(-5 = 24t – 5t^2\)
\(5t^2 – 24t – 5 = 0\)
\((t – 5)(5t + 1) = 0\)
This gives two potential solutions: \(t = 5\) and \(t = -1/5\). However, since time cannot be negative in this physical context, we discard the \(t = -1/5\) solution.
Time of Ascent:\(0 = 24 – 10t_1 \rightarrow t_1 = 2.4\)
This equation represents the time it takes for the particle to reach its maximum height during the ascent.
Height at the Maximum Point:\(0 = 24^2 + 2(-10)h \rightarrow h = 28.8\)
This equation represents the height at the maximum point of the particle’s motion.
Time of Descent: Use the equation for free fall to find the time of descent (\(t_2\)):
\(33.8 = \frac{1}{2}gt_2^2 \rightarrow t_2 = 2.6\)
This equation relates the final velocity at the maximum height (\(0 \, \text{m/s}\)) to the acceleration due to gravity (\(-9.8 \, \text{m/s}^2\)) during descent.
Total Time of Flight: Sum the times of ascent and descent to get the total time of flight:
\(t = t_1 + t_2 = 2.4 + 2.6 = 5\)
This confirms that the total time of flight is \(5\) seconds.
In summary, the particle is projected upwards, reaching its maximum height at \(t = 2.4\) seconds, and then it descends back to the ground at \(t = 5\) seconds. The height at the maximum point is \(28.8\) meters.
Question
A particle P moves in a straight line starting from a point O. At time ts after leaving O, the displacement s m from O is given by s = \(t^{3} − 4t^{2} + 4t\) and the velocity is \(v m s^{−1}\).
(i) Find an expression for v in terms of t.
(ii) Find the two values of t for which P is at instantaneous rest.
(iii) Find the minimum velocity of P.
▶️Answer/Explanation
(i)The velocity (\(v\)) is the derivative of displacement (\(s\)) with respect to time (\(t\)). Therefore,
\(v = \frac{ds}{dt}\)
Given \(s = t^3 – 4t^2 + 4t\), we can find \(v\) by taking the derivative:
\(v = \frac{d}{dt}(t^3 – 4t^2 + 4t)\)
\(v = 3t^2 – 8t + 4\)
So, the expression for \(v\) in terms of \(t\) is \(v = 3t^2 – 8t + 4\).
(ii) For a particle to be at instantaneous rest, the velocity (\(v\)) must be zero. Therefore, set \(v = 0\) and solve for \(t\):
\(3t^2 – 8t + 4 = 0\)
Factor the quadratic equation:
\((3t – 2)(t – 2) = 0\)
This gives two solutions: \(t = \frac{2}{3}\) and \(t = 2\).
So, the particle is at instantaneous rest at \(t = \frac{2}{3}\) and \(t = 2\).
(iii)The minimum velocity occurs at the time when the particle is at instantaneous rest. From part (ii), we found that the particle is at instantaneous rest at \(t = \frac{2}{3}\) and \(t = 2\).
\(3\left(t^2 – \frac{8}{3}t\right) + 4\)
\(t^2 – \frac{8}{3}t = \left(t – \frac{4}{3}\right)^2 – \left(\frac{4}{3}\right)^2\)
\(3\left(t^2 – \frac{8}{3}t\right) + 4 = 3\left[\left(t – \frac{4}{3}\right)^2 – \left(\frac{4}{3}\right)^2\right] + 4\)
\(= 3\left(t – \frac{4}{3}\right)^2 – 3\left(\frac{4}{3}\right)^2 + 4\)
\(= 3\left(t – \frac{4}{3}\right)^2 – \frac{16}{3} + 4\)
\(= 3\left(t – \frac{4}{3}\right)^2 – \frac{4}{3}\)
Now, this expression is in the form \(3\left(t – \frac{4}{3}\right)^2 + \text{constant}\), which represents a parabolic function.
The minimum value of this function occurs when \(t – \frac{4}{3} = 0\), which means \(t = \frac{4}{3}\).
So, the minimum value of \(v\) occurs at \(t = \frac{4}{3}\), and substituting this into the expression, we get:
\(v = 3\left(\frac{4}{3} – \frac{4}{3}\right)^2 – \frac{4}{3} = -\frac{4}{3}\)
The particle reaches its minimum velocity of \(-\frac{4}{3}\) at \(t = \frac{4}{3}\). The quadratic term \(\left(t – \frac{4}{3}\right)^2\) represents the squared difference from the time when the particle is at instantaneous rest (\(t = \frac{4}{3}\)), and the coefficient 3 determines the steepness of the parabola.
Question
A particle starts from a point O and moves in a straight line. The velocity of the particle at time ts after leaving O is v m \(s^{−1}\), where

(i) Find the acceleration of the particle during the first 5 seconds of motion.
(ii) Find the value of t when the particle is instantaneously at rest.
(iii) Find the total distance travelled by the particle in the first 10 seconds of motion.
▶️Answer/Explanation
(i)Acceleration during the first 5 seconds:
The acceleration (\(a\)) is found by taking the derivative of the velocity function \(v(t)\) with respect to time \(t\).
In this case, \(v(t) = 1.5 + 0.4t\). The derivative of this function with respect to \(t\) is \(0.4\), which means the acceleration is a constant \(0.4 \, \mathrm{m/s^2}\).
(ii)To find when the particle is at rest, we set the velocity \(v(t)\) to zero and solve for \(t\):
\(\frac{100}{t^2} – 0.1t = 0\)
\(100 – 0.1t^3 = 0\)
\(t^3 = \frac{100}{0.1} = 1000\)
\(t = \sqrt[3]{1000} = 10 \, \mathrm{s}\)
This is the time when the particle is instantaneously at rest.
(iii)The distance traveled is found by integrating the absolute value of the velocity function over the given time intervals. There are two intervals: \(0 \leq t \leq 5\) and \(5 \leq t \leq 10\).
For the first interval:
\(s_1 = \frac{1}{2}(1.5 + 3.5) \times 5 = 12.5 \, \mathrm{m}\)
For the second interval:
\(s(t) = \int \left(\frac{100}{t^2} – 0.1t\right) \, dt = -\frac{100}{t} – 0.5t^2 + C\)
Evaluating \(s(t)\) at \(t = 10\) and \(t = 5\) and subtracting:
\(s(10) – s(5) = \left(-\frac{100}{10} – 0.5(10)^2\right) – \left(-\frac{100}{5} – 0.5(5)^2\right)\)= 6.25 \, \mathrm{m}\)
The total distance is the sum of \(s_1\) and the difference \(s(10) – s(5)\):
\(18.75 \, \mathrm{m} = 12.5 \, \mathrm{m} + 6.25 \, \mathrm{m}\)
So, the particle travels a total distance of \(18.75 \, \mathrm{m}\) in the first 10 seconds.
Question
The diagram shows the velocity-time graph of a particle which moves in a straight line. The graph consists of 5 straight line segments. The particle starts from rest at a point A at time t = 0, and initially travels towards point B on the line.
(i) Show that the acceleration of the particle between t = 3.5 and t = 6 is −10 m \(s^{−2}\).
(ii) The acceleration of the particle between t = 6 and t = 10 is 7.5 m\( s^{−2}\) . When t = 10 the velocity of the particle is V m \(s^{−1}\) . Find the value of V.
(iii) The particle comes to rest at B at time T s. Given that the total distance travelled by the particle between t = 0 and t = T is 100 m, find the value of T.
▶️Answer/Explanation
(i)Acceleration between \(t=3.5\) and \(t=6\):
\(a = \frac{\Delta v}{\Delta t} = \frac{-40}{2.5} = -10 \, \mathrm{m/s^2}\)
(ii) Velocity \(V\) at \(t=10\):
\(V = -15 + 7.5 \times 4 = 15 \, \mathrm{m/s}\)
(iii) Time \(T\) when the particle comes to rest:
The total distance traveled is the sum of the areas under the velocity-time graph. You correctly set up the equation using the areas of the three segments:
\(\frac{1}{2} \times (4.5 + 2) \times 10 + \frac{1}{2} \times (8 – 4.5) \times 15 + \frac{1}{2} \times (T – 8) \times 15 = 100\)
\(45 + 45 + \frac{15}{2} \times (T – 8) = 100\)
\(90 + \frac{15}{2} \times (T – 8) = 100\)
\(15(T – 8) = 20\)
\(T – 8 = \frac{4}{3}\)
\(T = 13.5\)
So, \(T = 13.5\) seconds when the particle comes to rest.
Question
A small ball is projected with speed \(15 ms^{-1}\)at an angle of 60Å above the horizontal. Find the distance
from the point of projection of the ball at the instant when it is travelling horizontally.
▶️Answer/Explanation
Vertical Component:
– \(u_y = 15 \sin(60^\circ)\)
– Use \(v_y = u_y – gt\) and solve for \(t\):
\(0 = 15 \sin(60^\circ) – 9.8t\)
\(t = \frac{15 \sin(60^\circ)}{9.8} \approx 1.30 \, \mathrm{s}\)
Horizontal Component:
– \(u_x = 15 \cos(60^\circ)\)
– \(R = u_x \times t\)
\(R = 15 \cos(60^\circ) \times 1.30 \approx 9.74 \, \mathrm{m}\)
Vertical Distance:
– \(y = \frac{{u_y}^2}{2g}\)
\(y = \frac{(15 \sin(60^\circ))^2}{2 \times 9.8} \approx 8.44 \, \mathrm{m}\)
Total Distance:
– Use the Pythagorean theorem:
\(D = \sqrt{9.74^2 + 8.44^2} \approx 12.9 \, \mathrm{m}\)
So, the distance from the point of projection when the ball is traveling horizontally is approximately \(12.9 \, \mathrm{m}\).
Question
A block of mass 3 kg is initially at rest on a smooth horizontal floor. A force of 12 N, acting at an angle of \(25^{\circ}\) above the horizontal, is applied to the block. Find the distance travelled by the block in the first 5 seconds of its motion.
▶️Answer/Explanation
Given:
– Force applied (\(F\)) = \(12 \, \mathrm{N}\)
– Mass of the block (\(m\)) = \(3 \, \mathrm{kg}\)
– Angle of the force (\(\theta\)) = \(25^\circ\)
– Time (\(t\)) = \(5 \, \mathrm{s}\)
Horizontal Component of Force:
\(F_{\text{horizontal}} = F \cos(\theta)\)
\(F_{\text{horizontal}} = 12 \cos(25^\circ)\)
\(F_{\text{horizontal}} \approx 12 \times 0.9063 \approx 10.874 \, \mathrm{N}\)
Acceleration (\(a\)) using Newton’s Second Law:
\(F_{\text{horizontal}} = ma\)
\(10.874 = 3a\)
\(a \approx \frac{10.874}{3} \approx 3.625 \, \mathrm{m/s^2}\)
Distance Traveled (\(d\)) using Kinematic Equation:
\(d = \frac{1}{2}at^2\)
\(d = \frac{1}{2} \times 3.625 \times (5)^2\)
\(d = 45.3125 \, \mathrm{m}\)
Question
A particle P moves in a straight line passing through a point O. At time ts, the velocity of P, v m\( s^{−1}\), is given by v = qt + rt2 , where q and r are constants. The particle has velocity 4 m s−1 when t = 1 and when t = 2.
(i) Show that, when t = 0.5, the acceleration of P is 4 m\( s^{−2}\).
(ii) Find the values of t when P is at instantaneous rest.
(iii) The particle is at O when t = 3. Find the distance of P from O when t = 0.
▶️Answer/Explanation
(i) Given the velocity function \(v = qt + rt^2\), we differentiate it to find the acceleration (\(a\)):
\(a = \frac{dv}{dt} = q + 2rt\)
At \(t = 0.5\):
\(a = q + 2r \times 0.5 = q + r\)
Given the information that \(a = 4\) at \(t = 0.5\), we set up the equations:
\(q + r = 4 \quad \text{(1)}\)
\(2q + 4r = 4 \quad \text{(2)}\)
Solving this system of equations, we find \(q = 6\) and \(r = -2\). Therefore, the velocity function is \(v = 6t – 2t^2\) and the acceleration function is \(a = 6 – 4t\).
(ii) To find the time when \(P\) is at instantaneous rest, we set \(v = 0\) and solve for \(t\):
\(v = 6t – 2t^2 = 0\)
\(2t(3 – t) = 0\)
This gives two solutions: \(t = 0\) and \(t = 3\). Thus, \(P\) is at rest at \(t = 0\) and \(t = 3\).
(iii) Distance from \(O\) at \(t = 0\):
Option 1:
\(s = \int (6t – 2t^2) \, dt = 3t^2 – \frac{2}{3}t^3 + C\)
Using the condition that \(s = 0\) at \(t = 3\), we find \(C = -9\). Therefore,
\(s = 3t^2 – \frac{2}{3}t^3 – 9\)
Substituting \(t = 0\), we get \(s = 9 \, \mathrm{m}\).
Option 2:
\(s = \int_0^3 (6t – 2t^2) \, dt = \left[3t^2 – \frac{2}{3}t^3\right]_0^3\)
Evaluating this, we get \(s = 9 \, \mathrm{m}\) as well.
Both options lead to the same result: the distance from \(O\) at \(t = 0\) is \(9 \, \mathrm{m}\).
Question
A particle P moves in a straight line ABCD with constant deceleration. The velocities of P at A, B and C are \(20 m s^{−1}\) , 12 \(m s^{−1}\) and \(6 m s^{−1}\) respectively.
(i) Find the ratio of distances AB : BC.
(ii) The particle comes to rest at D. Given that the distance AD is 80 m, find the distance BC
▶️Answer/Explanation
(i) Ratio of distances \(\mathrm{AB} : \mathrm{BC}\):
The kinematic equation relating initial velocity (\(u\)), final velocity (\(v\)), acceleration (\(a\)), and distance (\(s\)) is given by:
\(v^2 = u^2 + 2as\)
At point \(A\), \(v = 0\) and \(u = 20 \, \mathrm{m/s}\), and at point \(B\), \(v = 12 \, \mathrm{m/s}\) and \(u = 20 \, \mathrm{m/s}\).
Similarly, at point \(C\), \(v = 6 \, \mathrm{m/s}\) and \(u = 12 \, \mathrm{m/s}\).
Applying the kinematic equation for \(\mathrm{AB}\):
\(0^2 = 20^2 – 2a \times \mathrm{AB}\)
\(\mathrm{AB} = \frac{20^2}{2a}\)
Applying the kinematic equation for \(\mathrm{BC}\):
\(12^2 = 20^2 – 2a \times \mathrm{BC}\):
\(\mathrm{BC} = \frac{54}{a}\)
Therefore, the ratio of distances \(\mathrm{AB} : \mathrm{BC}\) is given by:
\(\mathrm{AB} : \mathrm{BC} = \frac{20^2}{2a} : \frac{54}{a} = \frac{20^2}{2} : \frac{54}{1} = 64 : 27\)
(ii)Distance \(\mathrm{BC}\) when the particle comes to rest at \(D\):
Given that the particle comes to rest at \(D\), \(v = 0\) at \(D\), and \(u = 20 \, \mathrm{m/s}\) at \(A\). Applying the kinematic equation:
\(0^2 = 20^2 – 2a \times \mathrm{AD}\)
\(a = \frac{20^2}{2 \times \mathrm{AD}} = \frac{20^2}{2 \times 80} = 2.5 \, \mathrm{m/s^2}\)
Now that we know \(a\), we can find \(\mathrm{BC}\) using the equation for \(\mathrm{BC}\):
\(\mathrm{BC} = \frac{54}{a} = \frac{54}{2.5} = 21.6 \, \mathrm{m}\)
A cyclist starts from rest at a fixed point O and moves in a straight line, before coming to rest k seconds later. The acceleration of the cyclist at time ts after leaving O is am s−2, where a = \(2t^{-\frac{1}{2}} – \frac{3}{5}t^{\frac{1}{2}}\) for 0 < t ≤ k.
(a) Question
Find the value of k.
▶️Answer/Explanation
(a)The given acceleration function is \(a = 2t^{-\frac{1}{2}} – \frac{3}{5}t^{\frac{1}{2}}\). To find the time \(k\) when the cyclist comes to rest, we integrate this acceleration function with respect to time to get the velocity function \(v\):
\(v = \int (2t^{-\frac{1}{2}} – \frac{3}{5}t^{\frac{1}{2}}) \, dt\)
Integrating each term separately, we get:
\(v = 4t^{\frac{1}{2}} – \frac{2}{3}t^{\frac{3}{2}} + C\)
Now, to find the time \(k\), we set \(v = 0\) because the cyclist comes to rest:
\(4t^{\frac{1}{2}} – \frac{2}{3}t^{\frac{3}{2}} = 0\)
Solving this equation gives \(t = 10\), so \(k = 10\).
(b) Question
Find the maximum speed of the cyclist.
▶️Answer/Explanation
(b)To find the maximum speed, we set the acceleration function \(a = 2t^{-\frac{1}{2}} – \frac{3}{5}t^{\frac{1}{2}}\) to zero because this is when the cyclist changes from acceleration to deceleration:
\(2t^{-\frac{1}{2}} – \frac{3}{5}t^{\frac{1}{2}} = 0\)
Solving this equation gives \(t = \frac{10}{3}\).
Now, we substitute this time back into the velocity function:
\(v = 4t^{\frac{1}{2}} – \frac{2}{3}t^{\frac{3}{2}}\)
Substituting \(t = \frac{10}{3}\) gives \(v \approx 4.87 \, \mathrm{m/s}\).
(c) Question
Find an expression for the displacement from O in terms of t. Hence find the total distance travelled by the cyclist from the time at which she reaches her maximum speed until she comes to rest.
▶️Answer/Explanation
(c)To find the displacement function \(s\), we integrate the velocity function:
\(s = \int (4t^{\frac{1}{2}} – \frac{2}{3}t^{\frac{3}{2}}) \, dt\)
Integrating each term separately, we get:
\(s = \frac{8}{3}t^{\frac{3}{2}} – \frac{4}{25}t^{\frac{5}{2}} + C\)
Now, we substitute the values of \(t\) at the two relevant points: \(t = \frac{10}{3}\) and \(t = 10\):
\(s = \frac{8}{3} \times \left(\frac{10}{3}\right)^{\frac{3}{2}} – \frac{4}{25} \times \left(\frac{10}{3}\right)^{\frac{5}{2}} + C\)
\(s \approx 20.7 \, \mathrm{m}\)
This represents the total distance traveled from the time the cyclist reaches the maximum speed until coming to rest.
Question
A particle P is projected vertically upwards from horizontal ground with speed u m s−1. P reaches a maximum height of 20 m above the ground.
(a) Find the value of u.
▶️Answer/Explanation
(a) When a particle is projected vertically upwards, the maximum height (\(H\)) reached can be related to the initial speed (\(u\)) using the kinematic equation:
\(H = \frac{u^2}{2g}\)
where \(g\) is the acceleration due to gravity (\(9.8 \, \mathrm{m/s^2}\)).
Given that \(H = 20 \, \mathrm{m}\), we can solve for \(u\):
\(20 = \frac{u^2}{2 \times 9.8}\)
\(u^2 = 20 \times 2 \times 9.8\)
\(u^2 = 392\)
\(u = \sqrt{392}\)
\(u \approx 19.8 \, \mathrm{m/s}\)
So, the initial speed \(u\) is approximately \(19.8 \, \mathrm{m/s}\)
(b) Question
Find the total time for which P is at least 15m above the ground.
▶️Answer/Explanation
(b)We know that the vertical motion of the particle can be described by the equation:
\(h(t) = ut – \frac{1}{2}gt^2\)
where:
– \(h(t)\) is the height at time \(t\),
– \(u\) is the initial vertical speed,
– \(g\) is the acceleration due to gravity.
In this case, \(u\) is the initial speed with which the particle is projected vertically upwards.
Given that \(h(t) = 20 \, \mathrm{m}\) (maximum height), we can set up the equation:
\(20 = ut – \frac{1}{2} \times 10 \times t^2\)
Solving this quadratic equation gives two solutions for \(t\): \(t = 1\) or \(t = 3\).
Now, the total time \(T_{\text{total}}\) is the sum of the time taken to reach the maximum height (\(T_1\)) and the time taken to descend from the maximum height to a height of \(15 \, \mathrm{m}\) (\(T_2\)):
\(T_{\text{total}} = T_1 + T_2 = \frac{u}{g} + \sqrt{\frac{2h}{g}}\)
Substituting \(u = 20 \, \mathrm{m/s}\), \(g = 10 \, \mathrm{m/s^2}\), and \(h = 20 \, \mathrm{m} – 15 \, \mathrm{m} = 5 \, \mathrm{m}\), we get \(T_{\text{total}} = 2 \, \mathrm{s}\).
A particle P moves in a straight line starting from a point O and comes to rest 14 s later. At time t s after leaving O, the velocity v m s−1 of P is given by
v = pt2 − qt 0 ≤ t ≤ 6,
v = 63 − 4.5t 6 ≤ t ≤ 14,
where p and q are positive constants.
The acceleration of P is zero when t = 2.
(a) Question
Given that there are no instantaneous changes in velocity, find p and q.
▶️Answer/Explanation
(a) The given acceleration \(a\) is related to the velocity function \(v\) by the equation \(a = \frac{dv}{dt}\). We can find \(p\) and \(q\) by integrating \(a\) with respect to \(t\).
\(a(t) = 2p t – q\)
Integrating \(a\) with respect to \(t\) gives \(v(t)\):
\(v(t) = \int (2p t – q) \, dt = p t^2 – qt + C\)
Given that there are no instantaneous changes in velocity, we can find \(p\) and \(q\) by matching the coefficients of the terms in \(v(t)\) to the given velocity functions for the intervals \([0, 6]\) and \([6, 14]\).
For \(0 \leq t \leq 6\), \(v(t) = pt^2 – qt\), and for \(6 \leq t \leq 14\), \(v(t) = 63 – 4.5t\).
Equating coefficients, we get the system of equations:
\(36p – 6q = 36\)
\(4p – q = 0\)
Solving this system, we find \(p = 3\) and \(q = 12\).
(b) Question
Sketch the velocity-time graph.
▶️Answer/Explanation
(b) The velocity function is given by:
\(v(t) = \begin{cases} pt^2 – qt, & \text{for } 0 \leq t \leq 6 \\ 63 – 4.5t, & \text{for } 6 \leq t \leq 14 \end{cases}\)
We have a correct quadratic from \(t = 0\) to \(t = 6\) (opening upwards) and a correct straight line from \(t = 6\) to \(t = 14\) (with negative slope). The sketch should show key points like the vertex of the quadratic and the intersection of the quadratic and the straight line.
(c) Question
Find the total distance travelled by P during the 14 s.
▶️Answer/Explanation
(c)The displacement function \(s(t)\) is the antiderivative of the velocity function \(v(t)\). We integrate \(v(t)\) for each interval separately.
For \([0, 6]\):
\(s(t) = \int (pt^2 – qt) \, dt = \left| \frac{1}{3}pt^3 – \frac{1}{2}qt^2 \right| \Big|_0^6\)
For \([6, 14]\):
\(s(t) = \int (63 – 4.5t) \, dt = \left[63t – 2.25t^2\right]_6^{14} = 144\)
The total distance traveled is the sum of the magnitudes of these displacements:
\(S_{\text{total}} = |s(6)| + |s(14)| + \text{area of triangle}\)
\(S_{\text{total}} = \left|63 \times 6 – 2.25 \times 6^2\right| + \left|63 \times 14 – 2.25 \times 14^2\right| + \frac{1}{2} \times 8 \times 12\)
Evaluating this expression, we get \(S_{\text{total}} = 208 \, \mathrm{m}\).
A bus moves from rest with constant acceleration for 12 s. It then moves with constant speed for 30 s before decelerating uniformly to rest in a further 6 s. The total distance travelled is 585 m.
(a) Question
Find the constant speed of the bus.
▶️Answer/Explanation
(a)The motion of the bus is divided into three phases: acceleration, constant speed, and deceleration.
For the acceleration phase (first 12 seconds):
\(s_1 = \frac{1}{2} a_1 t_1^2\)
\(s_1 = \frac{1}{2} a_1 (12)^2\)
For the constant speed phase (next 30 seconds):
\(s_2 = v \cdot t_2\)
\(s_2 = 30v\)
For the deceleration phase (last 6 seconds):
\(s_3 = v \cdot t_3 + \frac{1}{2} a_2 t_3^2\)
\(s_3 = v \cdot 6 + \frac{1}{2} a_2 (6)^2\)
The total distance traveled is the sum of these distances:
\(s_{\text{total}} = s_1 + s_2 + s_3\)
Given that \(s_{\text{total}} = 585\), we can write the equation:
\(\frac{1}{2} a_1 (12)^2 + 30v + 6v + \frac{1}{2} a_2 (6)^2 = 585\)
Now, we know that \(a_1 = \frac{v}{t_1}\), where \(t_1 = 12\), so we substitute this into the equation:
\(\frac{1}{2} \left(\frac{v}{12}\right) (12)^2 + 30v + 6v + \frac{1}{2} a_2 (6)^2 = 585\)
Solving this equation, we find that \(v = 15 \mathrm{~ms^{-1}}\).
(b) Question
Find the magnitude of the deceleration.
▶️Answer/Explanation
(b) The deceleration is given by \(a_2 = \frac{v}{t_3}\), where \(t_3 = 6\):
\(a_2 = \frac{15}{6} = 2.5 \mathrm{~ms^{-2}}\)
So, the magnitude of the deceleration is \(2.5 \mathrm{~ms^{-2}}\).
Question
A particle moving in a straight line starts from rest at a point A and comes instantaneously to rest at a
point B. The acceleration of the particle at time t s after leaving A is am s−2, where
\(a=6t^{\frac{1}{2}}-2t\)
(a) Find the value of t at point B.
(b) Find the distance travelled from A to the point at which the acceleration of the particle is again
zero.
▶️Answer/Explanation
(a)We start with the expression for velocity (\(v\)) as the integral of acceleration (\(a\)) with respect to time (\(t\)):
\(v = \int (6t^{\frac{1}{2}} – 2t) \, dt\)
Integrating, we get:
\(v = 4t^{\frac{3}{2}} – t^2 + C\)
The constant of integration (\(C\)) is determined by the initial condition.
At \(t = 0\), the particle starts from rest, so \(v = 0\):
\(0 = 4(0)^{\frac{3}{2}} – (0)^2 + C\)
This implies \(C = 0\), and the velocity function becomes:
\(v = 4t^{\frac{3}{2}} – t^2\)
Now, to find the time \(t\) at point B, set \(v = 0\):
\(0 = 4t^{\frac{3}{2}} – t^2\)
Factor out \(t^2\) from both terms:
\(0 = t^2(4t^{\frac{1}{2}} – 1)\)
This equation is satisfied when \(t = 0\) (initial condition) or \(4t^{\frac{1}{2}} – 1 = 0\). Solving \(4t^{\frac{1}{2}} – 1 = 0\) gives \(t = 16\), which is the time at which the particle comes to rest again. Therefore, \(t = 16\) is the value of \(t\) at point B.
(b)The distance traveled (\(s\)) is given by the integral of velocity with respect to time:
\(s = \int v \, dt\)
Substitute the expression for \(v\):
\(s = \int (4t^{\frac{3}{2}} – t^2) \, dt\)
Integrate each term separately:
\(s = \frac{8}{5}t^{\frac{5}{2}} – \frac{1}{3}t^3 + C\)
Now, evaluate this expression from \(t = 0\) to \(t = 16\) to find the distance traveled:
\(s = \left[\frac{8}{5}\left(16\right)^{\frac{5}{2}} – \frac{1}{3}(16)^3\right] – \left[\frac{8}{5}(0)^{\frac{5}{2}} – \frac{1}{3}(0)^3\right]\)
Solving this expression gives \(s = 145.8\) meters. This is the total distance traveled from point A to the point where the acceleration is again zero.
Question
Two cyclists, Isabella and Maria, are having a race. They both travel along a straight road with constant acceleration, starting from rest at point A. Isabella accelerates for 5 s at a constant rate am s−2. She then travels at the constant speed she has reached for 10 s, before decelerating to rest at a constant rate over a period of 5 s.
Maria accelerates at a constant rate, reaching a speed of 5 m s−1 in a distance of 27.5 m. She then maintains this speed for a period of 10 s, before decelerating to rest at a constant rate over a period of 5 s.
(a) Given that a = 1.1, find which cyclist travels further.
(b) Find the value of a for which the two cyclists travel the same distance.
▶️Answer/Explanation
(a) For Isabella, we use the equations of motion to find the distance traveled during each phase:
Acceleration phase (first 5 seconds):
\(S_I = \frac{1}{2} \times 1.1 \times 5^2 + 10 \times 5.5 + \frac{1}{2} \times 1.1 \times 5^2 = 82.5 \ \mathrm{m}\)
or using the average speed formula \(\text{Average speed} = \frac{\text{Total distance}}{\text{Total time}}\):
\(S_I = \frac{1}{2} \times (20 + 10) \times 5.5 = 82.5 \ \mathrm{m}\)
For Maria:
Acceleration phase (first 5 seconds):
\(S_M = 27.5 + 5 \times 10 + \frac{1}{2} \times 5 \times 5 = 90 \ \mathrm{m}\)
So, Maria travels further with a total distance of \(90 \ \mathrm{m}\) compared to Isabella’s \(82.5 \ \mathrm{m}\).
(b) Setting the total distances equal to each other and solving for \(a\):
\(\frac{1}{2} \times 1.2 \times 5^2 + 10 \times 5 \times 1.2 + \frac{1}{2} \times 1.2 \times 5^2 = 90\)
or
\(\frac{1}{2} \times (20 + 10) \times 5 \times 1.2 = 90\)
Solving this equation gives \(a = 1.2 \ \mathrm{m/s^2}\).
Question
A particle moves in a straight line. It starts from rest from a fixed point O on the line. Its velocity at times t s after leaving O is \(vms^{-1}\), where \(v=t^2-8t^{\frac{3}{2}}+10t\).
(a) Find the displacement of the particle from O when t=1.
(b) Show that the minimum velocity of the particle is \(-125ms^{-1}\).
▶️Answer/Explanation
(a) Displacement at \(t = 1\):
Given velocity function \(v(t) = t^2 – 8t^{3/2} + 10t\), we want to find the displacement function \(s(t)\) by integrating \(v(t)\) with respect to \(t\):
\( s(t) = \int v(t) \, dt \)
\( s(t) = \int (t^2 – 8t^{3/2} + 10t) \, dt \)
Integrating term by term:
\( s(t) = \frac{1}{3}t^3 – \frac{16}{5}t^{5/2} + 5t^2 + C \)
Now, to find the displacement at \(t = 1\), substitute \(t = 1\) into \(s(t)\):
\( s(1) = \frac{1}{3}(1)^3 – \frac{16}{5}(1)^{5/2} + 5(1)^2 + C \)
\( s(1) = \frac{1}{3} – \frac{16}{5} + 5 + C \)
Now, the constant of integration (\(C\)) is irrelevant for finding the change in displacement, so we can ignore it.
\( s(1) = \frac{1}{3} – \frac{16}{5} + 5 \)
\( s(1) = 2.13 \, \text{m} \ \)
(b)Given the velocity function \(v(t) = t^2 – 8t^{3/2} + 10t\), we want to find the critical points by setting the derivative equal to zero:
\( v'(t) = 2t – 6t^{1/2} + 10 = 0 \)
Solving for \(t\):
\( 2t – 6t^{1/2} + 10 = 0 \)
\( 2(t^{1/2} – 5)(t^{1/2} – 1) = 0 \)
This gives \(t = 1\) or \(t = 25\). Now, we need to check the second derivative to determine whether each critical point is a minimum or maximum:
\( a”(t) = \frac{d^2 a}{d t^2} = -6t^{-1/2} \)
Evaluating \(a”(t)\) at \(t = 25\):
\( a”(25) = -6 \times 25^{-1/2} = -6 \times \frac{1}{5} = -\frac{6}{5} < 0 \)
Since \(a”(25) < 0\), \(t = 25\) corresponds to a minimum.
Now, substitute \(t = 25\) into the velocity function to find the minimum velocity:
\( v(25) = 25^2 – 8 \times 25^{3/2} + 10 \times 25 = -125 \, \text{m/s}^{-1} \)
So, the minimum velocity is \(-125 \, \text{m/s}^{-1}\).
Question
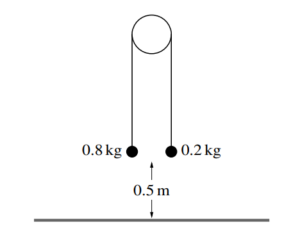
Two particles of masses 0.8 kg and 0.2 kg are connected by a light inextensible string that passes over
a fixed smooth pulley. The system is released from rest with both particles 0.5 m above a horizontal
floor (see diagram). In the subsequent motion the 0.2 kg particle does not reach the pulley.
(a) Show that the magnitude of the acceleration of the particles is 6 m s−2 and find the tension in the
string.
(b) When the 0.8 kg particle reaches the floor it comes to rest.
Find the greatest height of the 0.2 kg particle above the floor.
▶️Answer/Explanation
(a) Acceleration and Tension:
We start by applying Newton’s second law to each mass in the system.
For the \(0.8 \, \text{kg}\) mass (let’s call it Mass 1), the equation is:
\(0.8g – T = 0.8a\)
For the \(0.2 \, \text{kg}\) mass (let’s call it Mass 2), the equation is:
\(T – 0.2g = 0.2a\)
Now, for the system as a whole, we consider both masses together. The net force is the difference between the force acting on Mass 1 and the force acting on Mass 2:
\(0.8g – 0.2g = (0.8 + 0.2) a\)
\(0.6g = 1a\)
\(a = \frac{0.6g}{1} = 6 \, \text{m/s}^2\)
Now, let’s use this value of acceleration to find the tension (\(T\)) in the string. We can use either of the equations for Mass 1 or Mass Using the equation for Mass 1:
\(0.8g – T = 0.8 \times 6\)
\(T = 0.8g – 0.8 \times 6\)
\(T = 0.8 \times (9.8 – 6)\)
\(T = 3.2 \, \text{N}\)
So, the acceleration of the system is \(6 \, \text{m/s}^2\) and the tension in the string is \(3.2 \, \text{N}\).
(b) Greatest Height of the \(0.2 \, \text{kg}\) Particle:
Now that we know the acceleration of the system (\(6 \, \text{m/s}^2\)), we can use it to find the time (\(t\)) it takes for the \(0.8 \, \text{kg}\) particle to reach the floor.
\(v = u + at\)
\(0 = 6 – 20t\)
\(t = \frac{6}{20} = 0.3 \, \text{s}\)
Now, we can use this time to find the greatest height of the \(0.2 \, \text{kg}\) particle.
The greatest height (\(h\)) is given by:
\(h = ut + \frac{1}{2}at^2\)
\(h = 0 \times 0.3 + \frac{1}{2} \times 6 \times (0.3)^2\)
\(h = 0.45 \, \text{m}\)
So, the greatest height reached by the \(0.2 \, \text{kg}\) particle is \(1.3 \, \text{m}\) (0.5 m above the floor + 0.5 m below the starting point + 0.3 m above the starting point).
Question
A particle P moves in a straight line. It starts from rest at a point O on the line and at time t s after
leaving O it has acceleration a m s−2, where a = 6t − 18.
Find the distance P moves before it comes to instantaneous rest.
▶️Answer/Explanation
Given acceleration \(a = 6t – 18\), we want to find the distance \(P\) moves before it comes to instantaneous rest.
Integrating the acceleration function with respect to time to obtain the velocity function:
\(v = \int a \, dt = \int (6t – 18) \, dt \)
\( v = 3t^2 – 18t + C_1 \)
Here, \(C_1\) is the constant of integration.
Applying Initial Condition for Velocity
Since \(P\) starts from rest at \(O\), the initial velocity (\(v_0\)) is 0. Therefore, \(C_1 = 0\), and the velocity function becomes:
\( v = 3t^2 – 18t \)
Integrating the velocity function with respect to time to obtain the displacement function:
\( s = \int v \, dt = \int (3t^2 – 18t) \, dt \)
\( s = t^3 – 9t^2 + C_2 \)
Here, \(C_2\) is the constant of integration.
Applying Initial Condition for Displacement
Since \(P\) starts from rest at \(O\), the initial displacement (\(s_0\)) is 0. Therefore, \(C_2 = 0\), and the displacement function becomes:
\( s = t^3 – 9t^2 \)
Set the velocity \(v\) to zero to find the time \(t\) when the particle comes to instantaneous rest:
\( 3t^2 – 18t = 0 \)
\( 3t(t – 6) = 0 \)
This gives two solutions: \(t = 0\) and \(t = 6\).
Since the particle starts from rest, the relevant solution is \(t = 6\).
Substitute \(t = 6\) into the displacement function to find the distance \(P\) moves:
\( s = 6^3 – 9 \times 6^2 \)
\( s = 108 \, \text{m} \)
Therefore, the distance \(P\) moves before it comes to instantaneous rest is \(108 \, \text{m}\).
Question
A particle moves in a straight line AB. The velocity vm s−1 of the particle t s after leaving A is given
by v = k(t2 − 10t + 21), where k is a constant. The displacement of the particle from A, in the direction
towards B, is 2.85 m when t = 3 and is 2.4 m when t = 6.
(a) Find the value of k. Hence find an expression, in terms of t, for the displacement of the particle
from A.
(b) Find the displacement of the particle from A when its velocity is a minimum.
▶️Answer/Explanation
(a)Given the velocity function \(v = k(t^2 – 10t + 21)\), we want to find the value of \(k\) and the displacement function \(s\) in terms of \(t\).
Integrating velocity Function to Find \(s\):
\( s = \int v \, dt = \int k(t^2 – 10t + 21) \, dt \)
\( s = k\left(\frac{1}{3} t^3 – \frac{5}{2} t^2 + 21t\right) + C \)
Use the given information at \(t = 3\) and \(t = 6\) to set up a system of equations:
\( 2.85 = k\left(\frac{1}{3} \times 3^3 – \frac{5}{2} \times 3^2 + 21 \times 3\right) + C \)
\( 2.4 = k\left(\frac{1}{3} \times 6^3 – \frac{5}{2} \times 6^2 + 21 \times 6\right) + C \)
Solve this system to find \(k\) and \(C\).
\(k = 0.05\) and \(C = 1.5\).
Substituting \(k\) back into the Displacement Function:
Substituting \(k = 0.05\) back into the expression for \(s\):
\( s = 0.05\left(\frac{1}{3} t^3 – 5t^2 + 21t\right) + 1.5 \)
(b) Find the displacement when velocity is a minimum:
Differentiating the Velocity Function to Find Acceleration (\(a\)):
\( a = \frac{dv}{dt} = 0.05(2t – 10) \)
Set Acceleration \(a = 0\) to Find the Time \(t\):
\( 2t – 10 = 0 \)
Solving, you correctly found \(t = 5\).
Substitute \(t = 5\) back into the Displacement Function to Find \(s\):
Substitute \(t = 5\) into the expression for \(s\):
\( s = 0.05\left(\frac{1}{3} \times 5^3 – 5 \times 5^2 + 21 \times 5\right) + 1.5 \)
\( s = 2.58 \, \text{m} \)
Question
A particle P of mass 0.2 kg is released from rest at a point O on a plane inclined at 30° to the horizontal. At time t s after its release, P has velocity v m s−1 and displacement x m down the plane from O. The
coefficient of friction between P and the plane increases as P moves down the plane, and equals 0.1x2.
(i) Show that \(2v\frac{dv}{dx}=10-\left ( \sqrt{3} \right )x^{2}\) .
(ii) Calculate the maximum speed of P.
(iii) Find the value of x at the point where P comes to rest.
▶️Answer/Explanation
(i)The equation of motion along the incline is given by Newton’s second law:
\( F_{\text{net}} = ma \)
The net force \( F_{\text{net}} \) along the incline is the component of the gravitational force acting parallel to the incline minus the frictional force:
\( mgsin(30^\circ) – 0.1x^2 = ma \)
Where:
– \( m = 0.2 \, \text{kg} \) is the mass of the particle,
– \( g \) is the acceleration due to gravity,
– \( x \) is the displacement along the incline,
– \( a \) is the acceleration along the incline.
Now, the acceleration \( a \) can be expressed in terms of the velocity \( v \) and the displacement \( x \):
\( a = \frac{dv}{dt} = \frac{dv}{dx} \cdot \frac{dx}{dt} = v \cdot \frac{dv}{dx} \)
Thus, the equation becomes:
\( mgsin(30^\circ) – 0.1x^2 = mv \frac{dv}{dx} \)
Now, substitute \( g = 9.8 \, \text{m/s}^2 \) and \( sin(30^\circ) = \frac{1}{2} \):
\( 0.1x^2 = 0.2v \frac{dv}{dx} – 4.9 \)
\( x^2 = 2v \frac{dv}{dx} – 49 \)
\( x^2 + 49 = 2v \frac{dv}{dx} \)
\( 2v \frac{dv}{dx} = x^2 + 98 \)
\( 2v \frac{dv}{dx} = 98 – (\sqrt{3})x^2 \)
\( 2v \frac{dv}{dx} = 10 – (\sqrt{3})x^2 \)
(ii) Maximum Speed Calculation:
\(2\int v \, dv = \int (10 – \sqrt{3}x^2) \, dx\)
Integrating the left side
\(2\int v \, dv = v^2 + C_1\)
Here, \(C_1\) is the constant of integration.
Integrating the right side
\(\int (10 – \sqrt{3}x^2) \, dx = 10x – \frac{\sqrt{3}}{3}x^3 + C_2\)
Here, \(C_2\) is the constant of integration.
Now, substitute these results back into the original equation:
\(v^2 + C_1 = 10x – \frac{\sqrt{3}}{3}x^3 + C_2\)
Since we’re dealing with a definite integral and looking for the maximum speed, we can ignore the constants of integration (\(C_1\) and \(C_2\)) and proceed with the equation:
\(v^2 = 10x – \frac{\sqrt{3}}{3}x^3\)
Now, differentiate \(v^2\) with respect to \(x\) to find the critical points where \(\frac{dv}{dx} = 0\):
\(\frac{dv^2}{dx} = 10 – x^2\)
Set \(\frac{dv^2}{dx} = 0\) to find the critical points:
\(10 – x^2 = 0\)
\(x^2 = 10\)
\(x = \pm \sqrt{10}\)
However, we know that the particle is moving down the incline, so we consider the positive solution \(x = \sqrt{10}\).
Substitute \(x = \sqrt{10}\) into the expression for \(v^2\) to find the maximum speed:
\(v^2 = 10 \cdot \sqrt{10} – \frac{\sqrt{3}}{3} \cdot (\sqrt{10})^3\)
\(v^2 = 40 – \frac{10\sqrt{3}}{3}\)
\(v = \sqrt{40 – \frac{10\sqrt{3}}{3}}\)
\(v \approx 0.4 \, \text{m/s}\).
(iii) Particle Comes to Rest:
\(0 = 10x – \frac{\sqrt{3}}{3}x^3\)
This equation represents the condition when the particle comes to rest.
\(0 = x(10 – \frac{\sqrt{3}}{3}x^2)\)
This equation has two solutions: \(x = 0\) and \(x^2 = \frac{30}{\sqrt{3}}\).
The non-trivial solution for \(x\) (where the particle comes to rest) is:
\(x^2 = \frac{30}{\sqrt{3}}\)
\(x = \sqrt{\frac{30}{\sqrt{3}}} = \sqrt{\frac{30\sqrt{3}}{3}} = \sqrt{10\sqrt{3}}\)
Thus, the particle comes to rest at \(x = \sqrt{10\sqrt{3}}\).
Question
A particle P is projected vertically upwards with speed 5 m s−1 from a point A which is 2.8 m above
horizontal ground.
(a) Find the greatest height above the ground reached by P.
(b) Find the length of time for which P is at a height of more than 3.6 m above the ground.
▶️Answer/Explanation
(a)The motion of the particle is influenced by gravity. The key equation for vertical motion under gravity is given by:
\(v^2 = u^2 – 2gh\)
Where:
– \(v\) is the final velocity (0 m/s at the highest point),
– \(u\) is the initial velocity,
– \(g\) is the acceleration due to gravity (approximately \(9.8 \, \text{m/s}^2\)),
– \(h\) is the height.
In this case, the particle is projected vertically upwards, so \(v = 0\), \(u = 5 \, \text{m/s}\), and \(g = 9.8 \, \text{m/s}^2\).
\(0 = (5)^2 – 2 \cdot 9.8 \cdot h\)
\(h = \frac{(5)^2}{2 \cdot 9.8}\)
\(h \approx \frac{25}{19.6} \approx 1.28 \, \text{m}\)
The greatest height above the ground reached by \(P\) is approximately \(2.8 + 1.28 \, \text{m} = 4.08 \, \text{m}\).
(b) We’ll use the kinematic equation for vertical motion:
\(s = ut + \frac{1}{2}gt^2\)
Where:
– \(s\) is the displacement,
– \(u\) is the initial velocity,
– \(t\) is the time,
– \(g\) is the acceleration due to gravity.
In this case, \(s\) is the height above the ground, which is \(4.08 – 3.6 = 0.48 \, \text{m}\), \(u = 5 \, \text{m/s}\), and \(g = 9.8 \, \text{m/s}^2\).
\(0.48 = 5t + \frac{1}{2} \cdot 9.8 \cdot t^2\)
Solving for \(t\), we get a quadratic equation in the form \(at^2 + bt + c = 0\), where \(a = \frac{1}{2} \cdot 9.8\), \(b = 5\), and \(c = -0.48\). Using the quadratic formula:
\(t = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}\)
\(t = \frac{-5 \pm \sqrt{5^2 – 4 \cdot \frac{1}{2} \cdot 9.8 \cdot (-0.48)}}{2 \cdot \frac{1}{2} \cdot 9.8}\)
\(t \approx \frac{-5 \pm \sqrt{25 + 4 \cdot 9.8 \cdot 0.48}}{9.8}\)
\(t \approx \frac{-5 \pm \sqrt{25 + 19.6 \cdot 0.48}}{9.8}\)
\(t \approx \frac{-5 \pm \sqrt{25 + 9.408}}{9.8}\)
\(t \approx \frac{-5 \pm \sqrt{34.408}}{9.8}\)
\(t \approx \frac{-5 \pm 5.86}{9.8}\)
Now, we have two possible solutions for \(t\), but we discard the negative value since time cannot be negative in this context.
\(t \approx \frac{-5 + 5.86}{9.8} \approx \frac{0.86}{9.8} \approx 0.088 \, \text{s}\)
So, the time for which \(P\) is at a height of more than \(3.6 \, \text{m}\) above the ground is approximately \(0.088 \, \text{s}\).
Question
A particle moves in a straight line through the point O. The displacement of the particle from O at time ts is sm, where
\(s=t^2-3t+2\) for \(0 \leq t \leq 6\),
\(s=\frac{24}{t}-\frac{t^2}{4}+25\) for \(t \geq 6\)
(a) Find the value of t when the particle is instantaneously at rest during the first 6 seconds of its motion.
At t = 6, the particle hits a barrier at a point P and rebounds.
(b) Find the velocity with which the particle arrives at P and also the velocity with which the particle leaves P.
(c) Find the total distance travelled by the particle in the first 10 second of its motion.
▶️Answer/Explanation
(a) Given displacement function \(s = t^2 – 3t + 2\) for \(0 \leq t \leq 6\), we can find the velocity by taking the derivative of \(s\) with respect to \(t\):
\(v_1 = \frac{ds}{dt} = 2t – 3\)
To find when the particle is at rest (\(v_1 = 0\)), set \(2t – 3 = 0\) and solve for \(t\):
\(2t – 3 = 0\)
\(2t = 3\)
\(t = \frac{3}{2} = 1.5\)
So, the particle is instantaneously at rest at \(t = 1.5\) during the first 6 seconds.
(b) Given displacement function \(s = \frac{24}{t} – \frac{t^2}{4} + 25\) for \(t \geq 6\), we can find the velocity by taking the derivative of \(s\) with respect to \(t\):
\(v_2 = \frac{ds}{dt} = -\frac{24}{t^2} – \frac{t}{2}\)
At \(t = 6\), evaluate \(v_2\) to find the velocity when the particle arrives at \(P\):
\(v_{\text{arrive}} = -\frac{24}{6^2} – \frac{6}{2} = -5 \, \text{m/s}\)
Similarly, evaluate \(v_2\) just after \(t = 6\) to find the velocity when the particle leaves \(P\):
\(v_{\text{leave}} = -\frac{24}{(6^+)^2} – \frac{6^+}{2}\)
\(v_{\text{leave}} \approx -3.67 \, \text{m/s}\)
(c) Total Distance Travelled in the First 10 Seconds:
Given the displacement functions, let’s find the total distance traveled.
For \(0 \leq t \leq 6\):
\(d_1 = \int_{0}^{6} |2t – 3| \, dt\)
Evaluate this integral to find \(d_1\).
For \(t \geq 6\):
\(d_2 = \int_{6}^{10} \left|-\frac{24}{t^2} – \frac{t}{2}\right| \, dt\)
Evaluate this integral to find \(d_2\).
Finally, sum up \(d_1\) and \(d_2\) to get the total distance:
\(d_{\text{total}} = d_1 + d_2\)
\(d_1 = 2 \, \text{m}, \quad d_2 = 38.1 \, \text{m}\)
\(d_{\text{total}} = 40.1 \, \text{m}\)
Question
On a straight horizontal test track, driverless vehicles (with no passengers) are being tested. A car of mass 1600 kg is towing a trailer of mass 700kg along the track. The brakes are applied, resulting in a deceleration of 12\(ms^{-2}\). The braking force acts on the car only. In addition to the braking force there are constant resistance forces of 600N on the car and of 200N on the trailer.
(a) Find the magnitude of the force in the tow-bar.
(b) Find the braking force.
(c) At the instant when the brakes are applied, the car has speed 22\(ms^{-1}\). At this instant the car is 17.5 m away from a stationary van, which is directly in front of the car.
Show that the car hits the van at a speed of \(8ms^{-1}\).
(d) After the collision, the van starts to move with speed \(5ms^{-1}\) and the car and trailer continue moving in the same direction with speed \(2ms^{-1}\).
Find the mass of the van.
▶️ Answer/Explanation
(a) Magnitude of Force in the Tow-Bar:
The equation for the trailer is:
\(F_{\text{tow-bar}} – 200 = m_{\text{trailer}} \cdot a_{\text{trailer}}\)
Given that \(m_{\text{trailer}} = 700 \, \text{kg}\) and \(a_{\text{trailer}} = -12 \, \text{m/s}^2\) (since it’s decelerating), we can substituting the values:
\(F_{\text{tow-bar}} – 200 = 700 \cdot (-12) + 200\)
\(F_{\text{tow-bar}} = 8200 \, \text{N}\)
So, the magnitude of the force in the tow-bar is \(8200 \, \text{N}\).
(b) Braking Force:
For the car, the equation is:
\(F_{\text{braking}} – 600 = m_{\text{car}} \cdot a_{\text{car}}\)
Substitute \(m_{\text{car}} = 1600 \, \text{kg}\) and \(a_{\text{car}} = -12 \, \text{m/s}^2\):
\(F_{\text{braking}} – 600 = 1600 \cdot (-12) + 600\)
Now, solve for \(F_{\text{braking}}\):
\(F_{\text{braking}} = 26800 \, \text{N}\)
So, the braking force is \(26800 \, \text{N}\).
(c) Car Hits the Van:
Use the kinematic equation:
\(v_{\text{final}}^2 = v_{\text{initial}}^2 + 2a_{\text{car}}(x_{\text{final}} – x_{\text{initial}})\)
Substitute \(v_{\text{initial}} = 22 \, \text{m/s}\), \(a_{\text{car}} = -12 \, \text{m/s}^2\), \(x_{\text{initial}} = 17.5 \, \text{m}\), and \(v_{\text{final}} = 8 \, \text{m/s}\):
\(8^2 = 22^2 + 2 \cdot (-12) \cdot (x_{\text{final}} – 17.5)\)
Solve for \(x_{\text{final}}\):
\(x_{\text{final}} = 8.5 \, \text{m}\)
So, the car hits the van at a distance of \(8.5 \, \text{m}\).
(d)Use the conservation of momentum equation
\(m_{\text{car}} \cdot v_{\text{car, final}} + m_{\text{trailer}} \cdot v_{\text{trailer, final}} = m_{\text{van}} \cdot v_{\text{van, final}}\)
Substitute \(m_{\text{car}} = 1600 \, \text{kg}\), \(v_{\text{car, final}} = 2 \, \text{m/s}\), \(m_{\text{trailer}} = 700 \, \text{kg}\), \(v_{\text{trailer, final}} = 2 \, \text{m/s}\), \(v_{\text{van, final}} = 5 \, \text{m/s}\):
\(1600 \cdot 2 + 700 \cdot 2 = m_{\text{van}} \cdot 5\)
\(m_{\text{van}} = 2760 \, \text{kg}\)
So, the mass of the van is \(2760 \, \text{kg}\).
Question
A cyclist travels along a straight road with constant acceleration. He passes through points A, B and C. The cyclist takes 2 seconds to travel each of the sections AB and BC and passes through B with speed 4.5\(ms^{-1}\). The distance AB is \(\frac{4}{5}\) of the distance BC.
(a) Find the acceleration of the cyclist.
(b) Find AC.
▶️Answer/Explanation
(a)We have the equation:
\(2 \times 4.5 – \frac{1}{2}a(2)^2 = \frac{4}{5}(2 \times 4.5 + \frac{1}{2}a(2)^2)\)
\(9 – 2a = \frac{4}{5}(9 + 2a)\)
\(5(9 – 2a) = 4(9 + 2a)\)
\(45 – 10a = 36 + 8a\)
\(18a = 9\)
\(a = \frac{1}{2} \, \text{m/s}^2\)
So, the acceleration (\(a\)) is \(0.5 \, \text{m/s}^2\).
(b) Now that we have the value for \(a\), we can find the distance \(AC\) using the equation:
\(S_{AC} = S_{AB} + S_{BC}\)
\(S_{AC} = 2 \times 4.5 – \frac{1}{2} \times 0.5 \times 2^2 + 2 \times 4.5 + \frac{1}{2} \times 0.5 \times 2^2\)
\(S_{AC} = 8 \, \text{m}\)
So, the total distance \(AC\) is \(8 \, \text{m}\).
Question
A particle P moves in a straight line from a fixed point O. The velocity v \(ms^{-1}\) of P at time ts is given by \(v=t^{2}-8t+12\) for 0 ≤ t ≤ 8.
(i) Find the minimum velocity of P.
(ii) Find the total distance travelled by P in the interval
▶️Answer/Explanation
(i) The velocity function is given by \(v = t^2 – 8t + 12\). To find the minimum velocity, we need to find the critical points by setting the derivative equal to zero:
\(v’ = 2t – 8 = 0\)
Solving for \(t\):
\(2t = 8 \implies t = 4\)
Now, check the second derivative to confirm that \(t = 4\) corresponds to a minimum:
\(v” = 2\)
Since \(v”\) is positive, \(t = 4\) is a minimum point.
Now, substitute \(t = 4\) back into the original velocity function to find the minimum velocity:
\(v(4) = (4)^2 – 8(4) + 12\)
\(v(4) = 16 – 32 + 12 = -4\)
So, the minimum velocity of \(P\) is \(-4 \, \text{m/s}\).
(ii) To find the total distance traveled, we need to consider the displacement function. The displacement (\(s\)) is given by the antiderivative of the velocity function:
\(s(t) = \int v(t) \, dt\)
\(s(t) = \int (t^2 – 8t + 12) \, dt\)
\(s(t) = \frac{1}{3}t^3 – 4t^2 + 12t + C\)
Now, we need to find the constant of integration (\(C\)).
Since \(P\) starts from a fixed point \(O\), we know that \(s(0) = 0\). Substitute \(t = 0\) into the displacement function:
\(s(0) = \frac{1}{3}(0)^3 – 4(0)^2 + 12(0) + C\)
\(C = 0\)
So, the displacement function is:
\(s(t) = \frac{1}{3}t^3 – 4t^2 + 12t\)
Now, to find the total distance traveled, we need to find the points where the velocity changes direction. These points correspond to the roots of the velocity function:
\(t^2 – 8t + 12 = 0\)
\((t – 2)(t – 6) = 0\)
\(t = 2\) and \(t = 6\).
And we found that \(t = 2\) and \(t = 6\) are the points where the velocity changes direction.
Now, let’s calculate the total distance traveled using the correct intervals:
\(D = |s(2) – s(0)| + |s(6) – s(2)| + |s(8) – s(6)|\)
Substituting the values :
\(D = \left|\frac{1}{3}(2)^3 – 4(2)^2 + 12(2)\right| + \left|\frac{1}{3}(6)^3 – 4(6)^2 + 12(6)\right|\)
\(+ \left|\frac{1}{3}(8)^3 – 4(8)^2 + 12(8)\right|\)
\(D = \left|\frac{8}{3} – 16 + 24\right| + \left|\frac{216}{3} – 144 + 72\right| + \left|\frac{512}{3} – 256 + 96\right|\)
\(D = \left|\frac{32}{3}\right| + \left|\frac{32}{3}\right| + \left|\frac{32}{3}\right|\)
\(D = \frac{32}{3} + \frac{32}{3} + \frac{32}{3}\)
\(D = \frac{96}{3} = 32 \, \text{m}\)
So, the correct total distance traveled by \(P\) in the interval \([0, 8]\) is \(32 \, \text{m}\).
Question
A particle P is projected vertically upwards with speed \(25ms^{-1}\) from a point 3 m above horizontal ground.
(i) Find the time taken for P to reach its greatest height.
(ii) Find the length of time for which P is higher than 23 m above the ground.
(iii) P is higher than h m above the ground for 1 second. Find h.
▶️Answer/Explanation
(i)The vertical motion of the particle is governed by the kinematic equation:
\( v = u – gt \)
where:
– \(v\) is the final velocity,
– \(u\) is the initial velocity,
– \(g\) is the acceleration due to gravity (\(9.8 \, \mathrm{m/s^2}\)),
– \(t\) is the time.
At the greatest height, the final velocity \(v\) is \(0\).
The initial velocity \(u\) is given as \(25 \, \mathrm{m/s}\), and \(g\) is \(9.8 \, \mathrm{m/s^2}\).
\( 0 = 25 – 10t \)
\( t = \frac{25}{10} = 2.5 \, \mathrm{s} \)
(ii)The displacement \(s\) of the particle at any time \(t\) is given by the equation:
\( s = ut – \frac{1}{2}gt^2 \)
At the time \(t\) when the particle is \(23 \, \mathrm{m}\) above the ground, we set \(s\) to be \(23\) and solve for \(t\):
\( 23 = 25t – \frac{1}{2}(9.8)t^2 \)
\(t = 1\) and \(t = 4\).
However, we are interested in the time during the upward motion, so we choose the solution \(t = 4\).
The required time is the difference between the two times:
\( \text{Required time} = 4 – 1 = 3 \, \mathrm{s} \)
(iii)To find \(h\), we consider the time interval when \(P\) is higher than \(h\) for 1 second, which occurs during the upward and downward motions.
At the time \(t = 2.5 \, \mathrm{s}\) (when the particle reaches its greatest height), \(h\) above the ground is given by:
\( h = 25 \times (2.5)^2 = 31.25 \, \mathrm{m} \)
In the next 0.5 seconds, it falls a distance of \(1 / 2 \times 10 \times (0.5)^2 = 1.25 \, \mathrm{m}\). Therefore:
\( h = 31.25 – 1.25 = 30 \, \mathrm{m} \)
Question
A particle moves in a straight line. It starts from rest at a fixed point O on the line. Its acceleration at time ts after leaving O is a \(m s^{-2}\), where \(a = 0.4t^{3}-4.8t^{\frac{1}{2}}\)
(i) Show that, in the subsequent motion, the acceleration of the particle when it comes to instantaneous rest is 16 m s^{-2}
(ii) Find the displacement of the particle from O at t = 5
▶️Answer/Explanation
(i) Given the acceleration function \(a(t) = 0.4t^3 – 4.8t^{1/2}\), we need to find the velocity function \(v(t)\) by integrating the acceleration function with respect to time \(t\):
\( v(t) = \int (0.4t^3 – 4.8t^{1/2}) \, dt \)
\( v(t) = 0.1t^4 – 3.2t^{3/2} + C \)
Now, we set \(v(t) = 0\) to find the time when the particle comes to instantaneous rest:
\( 0.1t^4 – 3.2t^{3/2} = 0 \)
\( t^{3/2}(0.1t^{2} – 3.2) = 0 \)
This equation is satisfied when \( t^{3/2} = 0 \) (which gives \( t = 0 \), the initial time) or \( 0.1t^{2} – 3.2 = 0 \).
\( \( 0.1t^{2} – 3.2 = 0 \):
\( 0.1t^{2} = 3.2 \)
\( t^{2} = \frac{3.2}{0.1} \)
\( t^{2} = 32 \)
\( t = \sqrt{32} = 4\sqrt{2} \)
So, the time when the particle comes to instantaneous rest is \( t = 4\sqrt{2} \) seconds, and at that time, the acceleration is \( 16 \, \mathrm{m/s^{-2}} \).
(ii)The displacement function \(s(t)\) is given by integrating the velocity function:
\( s(t) = \int (0.1t^4 – 3.2t^{3/2}) \, dt \)
Integrating each term separately:
\( s(t) = 0.02t^5 – 1.28t^{5/2} + D \)
Now, to find the constant \(D\), we use the initial condition \(s(0) = 0\):
\( 0 = 0.02(0)^5 – 1.28(0)^{5/2} + D \)
This gives \(D = 0\), which is correct.
So, the displacement function is \(s(t) = 0.02t^5 – 1.28t^{5/2}\).
\( s(t) = 0.02t^5 – 1.28t^{5/2} + D \)
\( s(5) = \left[0.02 t^5 – 1.28 t^{5/2}\right]_0^5 \)
\( s(5) = \left[0.02 \cdot 5^5 – 1.28 \cdot 5^{5/2}\right] – \left[0.02 \cdot 0^5 – 1.28 \cdot 0^{5/2}\right] \)
\(s(5)=62.5-71.554\)
\( s(5) \approx -9.05 \, \text{meters} \)
Question
A particle is projected vertically upwards with speed \(30 ms^{-1}\)from a point on horizontal ground.
(i) Show that the maximum height above the ground reached by the particle is 45 m.
(ii) Find the time that it takes for the particle to reach a height of 33.75 m above the ground for the
first time. Find also the speed of the particle at this time.
▶️Answer/Explanation
(i) The particle is projected vertically upwards, so the only force acting on it is gravity.
The acceleration due to gravity (\(g\)) is directed downward and is approximately \(9.8 \, \mathrm{m/s^2}\).
The kinematic equation relating initial velocity (\(u\)), final velocity (\(v\)), acceleration (\(a\)), and displacement (\(s\)) is given by:
\( v^2 = u^2 + 2as \)
Since the particle is projected upwards, its final velocity at the highest point is \(0 \, \mathrm{m/s}\). The initial velocity (\(u\)) is \(30 \, \mathrm{m/s}\), and the acceleration (\(a\)) is \(-9.8 \, \mathrm{m/s^2}\) (negative because it acts downward).
Let \(s\) be the maximum height. We substitute these values into the equation:
\( 0 = (30)^2 + 2(-9.8)s \)
\( 900 = -19.6s \)
\( s = \frac{900}{19.6} \approx 45.92 \, \mathrm{m} \)
So, the maximum height above the ground reached by the particle is approximately \(45 \, \mathrm{m}\).
(ii) We are given the kinematic equation for vertical motion:
\( s = ut – \frac{1}{2}gt^2 \)
where:
– \(s\) is the displacement (in this case, \(33.75 \, \mathrm{m}\)),
– \(u\) is the initial velocity (\(30 \, \mathrm{m/s}\)),
– \(g\) is the acceleration due to gravity (\(9.8 \, \mathrm{m/s^2}\)),
– \(t\) is the time.
We set up the equation using the given values:
\( 33.75 = 30t – \frac{1}{2} \times 9.8 \times t^2 \)
\( 67.5 = 60t – 9.8t^2 \)
\( 9.8t^2 – 60t + 67.5 = 0 \)
\( t = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \)
For our quadratic equation \(9.8t^2 – 60t + 67.5 = 0\), the coefficients are \(a = 9.8\), \(b = -60\), and \(c = 67.5\).
\( t = \frac{60 \pm \sqrt{(-60)^2 – 4 \times 9.8 \times 67.5}}{2 \times 9.8} \)
\( t \approx \frac{60 \pm \sqrt{3600 – 2670}}{19.6} \)
\( t \approx \frac{60 \pm \sqrt{930}}{19.6} \)
\( t \approx \frac{60 \pm 30 \sqrt{3}}{19.6} \)
Since time cannot be negative in this context, we reject the negative solution:
\( t \approx \frac{60 + 30 \sqrt{3}}{19.6} \)
\( t \approx 1.5 \, \mathrm{s} \)
Now that we have the time, we can find the velocity at this time using the kinematic equation:
\( v = u – gt \)
\( v = 30 – 9.8 \times 1.5 \)
\( v = 30 – 14.7 \)
\( v = 15 \, \mathrm{m/s} \)
So, the time it takes for the particle to reach a height of \(33.75 \, \mathrm{m}\) is approximately \(1.5 \, \mathrm{s}\), and the speed of the particle at this time is \(15 \, \mathrm{m/s}\).
Question
A particle moves in a straight line starting from rest from a point O. The acceleration of the particle
at time ts after leaving O is a \(ms^{-2}\), where
a = 5.4 − 1.62t.
(i) Find the positive value of t at which the velocity of the particle is zero, giving your answer as an exact fraction.
(ii) Find the total distance travelled during the first ten seconds of the motion.
▶️Answer/Explanation
(i) The velocity function \(v(t) = 5.4t – 0.81t^2 + C\). Setting \(v(t) = 0\) gives:
\(5.4t – 0.81t^2 = 0\)
\(t(5.4 – 0.81t) = 0\)
This equation is satisfied when \(t = 0\) (initial time) or \(5.4 – 0.81t = 0\).
\(5.4 – 0.81t = 0\):
\(0.81t = 5.4\)
\(t = \frac{5.4}{0.81} = \frac{54}{81} = \frac{2}{3}\)
So, the positive value of \(t\) at which the velocity is zero is \(\frac{2}{3}\) seconds.
(ii)The displacement function \(s(t) = 2.7t^3 – 0.27t^3 + C\). To find the displacement at \(t = \frac{20}{3}\):
\(s\left(\frac{20}{3}\right) = 2.7\left(\frac{20}{3}\right)^3 – 0.27\left(\frac{20}{3}\right)^3 + C\)
\(s\left(\frac{20}{3}\right) = 40\)
So, the displacement at \(t = \frac{20}{3}\) is \(40\) meters.
The total distance traveled is twice the displacement because the particle moves in a straight line. Therefore:
\( \text{Total distance} = 2 \times 40 = 80 \, \mathrm{m} \)
Question
A particle P moves in a straight line. The velocity v \(m s^{−1}\) at time ts is given by
v = 4 + 0.2t for 0 ≤ t ≤ 10,
(i) Find the acceleration of P during the first 10 s.
(ii) Find the acceleration of P when t = 20.(iii) Sketch the velocity-time graph for 0 ≤ t ≤ 20.
(iv) Find the total distance travelled by P in the interval 0 ≤ t ≤ 20.
▶️Answer/Explanation
(i)The given velocity function is \(v(t) = 4 + 0.2t\). To find the acceleration, take the derivative of the velocity with respect to time (\(t\)):
\[a(t) = \frac{dv}{dt} = \frac{d}{dt}(4 + 0.2t) = 0.2 \, \mathrm{m/s^2}\]
So, the acceleration of \(P\) during the first \(10\) seconds is \(0.2 \, \mathrm{m/s^2}\).
(ii) The acceleration function remains constant throughout the entire interval, so the acceleration at \(t = 20\) is also \(0.2 \, \mathrm{m/s^2}\).
(iii) The velocity-time graph is a straight line with a constant slope equal to the acceleration. In this case, the acceleration is \(0.2 \, \mathrm{m/s^2}\), and the initial velocity is \(4 \, \mathrm{m/s}\). The graph will be a line that starts at \(t = 0\) with a velocity of \(4 \, \mathrm{m/s}\) and increases linearly with a slope of \(0.2\). It continues up to \(t = 20\) seconds.
Correct labelling on axes provided the curves
pass through (0,4), (10,6), (20,0)
(iv) Trapezium area = 50
\(\int (-800t^{-2})dt=-2t-800t^{-1}
\left [ -2t-800t^{-1} \right ]_{10}^{20}\)
=-40-40+20+80
Distance is 50 + 20 = 70 m
Question
A particle is projected from a point on horizontal ground. At the instant 2 s after projection, the particle has travelled a horizontal distance of 30 m and is at its greatest height above the ground. Find the initial speed and the angle of projection of the particle.
▶️Answer/Explanation
Given :
– The particle is projected from a point on horizontal ground.
– At \( t = 2 \) seconds, the particle has traveled a horizontal distance of \( 30 \) meters and is at its greatest height.
Let’s denote:
\( u \) as the initial speed of the particle,
\( \theta \) as the angle of projection.
Vertical motion equation:
\( v_y = u \sin(\theta) – gt \)
Horizontal motion equation:
\( S_x = u \cos(\theta) \times t \)
where:
– \( v_y \) is the vertical component of velocity,
– \( g \) is the acceleration due to gravity (\( 9.8 \, \mathrm{m/s^2} \)),
– \( S_x \) is the horizontal distance traveled,
– \( t \) is the time.
From the vertical motion equation, at \( t = 2 \) seconds, the vertical component of velocity (\( v_y \)) is \( 0 \) at the maximum height:
\( 0 = u \sin(\theta) – 2g \)
\( u \sin(\theta) = 2g \)
Given that \( g = 9.8 \, \mathrm{m/s^2} \):
\( u \sin(\theta) = 2 \times 9.8 \)
\( u \sin(\theta) = 19.6 \)
From the horizontal motion equation, the horizontal distance traveled (\( S_x \)) at \( t = 2 \) seconds is \( 30 \) meters:
\(30 = u \cos(\theta) \times 2 \)
\( u \cos(\theta) = 15 \)
Now, we have two equations:
\( u \sin(\theta) = 19.6 \) (Equation 1)
\( u \cos(\theta) = 15 \) (Equation 2)
From Equation 1 and Equation 2, we can find \( u \) by taking the square root of the sum of their squares:
\( u^2 = (u \sin(\theta))^2 + (u \cos(\theta))^2 \)
\( u^2 = 19.6^2 + 15^2 \)
\( u^2 = 384.16 + 225 \)
\( u^2 = 609.16 \)
\( u \approx \sqrt{609.16} \)
\( u \approx 24.66 \, \mathrm{m/s} \)
Now, we can find \( \theta \) using the tangent:
\( \tan(\theta) = \frac{u \sin(\theta)}{u \cos(\theta)} \)
\( \tan(\theta) = \frac{19.6}{15} \)
\( \theta \approx \tan^{-1}\left(\frac{19.6}{15}\right) \)
\( \theta \approx 53.1^\circ \)
So, the initial speed of the particle is approximately \( 24.66 \, \mathrm{m/s} \) and the angle of projection is approximately \( 53.1^\circ \).
Question
A stone is thrown with speed 9 m s−1 at an angle of 60° above the horizontal from a point on horizontal ground. Find the distance between the two points at which the path of the stone makes an angle of 45° with the horizontal.
▶️Answer/Explanation
Given:
– Initial speed (\(u\)) of the stone is \(9 \, \mathrm{m/s}\).
– Angle of projection (\(\theta\)) is \(60^\circ\).
The horizontal and vertical components of the initial velocity:
\( V_h = u \cos(60^\circ) = \frac{9}{2} \, \mathrm{m/s} \)
\( V_v = u \sin(60^\circ) = \frac{9\sqrt{3}}{2} \, \mathrm{m/s} \)
\( -V_v = V_v – gt \)
\( -\frac{9\sqrt{3}}{2} = \frac{9\sqrt{3}}{2} – 9.8t \)
\( -\frac{9\sqrt{3}}{2} = -9.8t \)
\( t = \frac{\frac{9\sqrt{3}}{2}}{9.8} \)
\( t \approx 0.43 \, \mathrm{s} \)
\( x = V_h t \)
\( x = \frac{9}{2} \times 0.43 \)
\( x \approx 1.935 \, \mathrm{m} \)
Question
A small rocket is fired vertically upwards, starting from rest at ground level, and moves with constant
acceleration. The rocket reaches a height of 200 m after 10 s.
(i) Show that the speed of the rocket after 10 s is 40 m \(s^{−1}\) and find the acceleration of the rocket
during the first 10 s.
(ii) After 10 s, the rocket’s fuel stops burning and there is no upward force acting on the rocket. Find the maximum height above ground level reached by the rocket.
(iii) Find the total time from the instant the rocket is fired until it returns to the ground.
▶️Answer/Explanation
(i) To find the speed (\(v\)) of the rocket after \(10 \, \mathrm{s}\) and the acceleration (\(a\)) during the first \(10 \, \mathrm{s}\), we can use the kinematic equation that relates initial velocity (\(u\)), final velocity (\(v\)), acceleration (\(a\)), and time (\(t\)):
\( v = u + at \)
Since the rocket starts from rest (\(u = 0\)), the equation simplifies to:
\( v = at \)
Given that the rocket reaches a height of \(200 \, \mathrm{m}\) after \(10 \, \mathrm{s}\), and using the kinematic equation for displacement (\(s\)) under constant acceleration:
\( s = ut + \frac{1}{2}at^2 \)
\( 200 = 0 + \frac{1}{2}a(10)^2 \)
\( a = \frac{2 \times 200}{10^2} \)
\( a = 4 \, \mathrm{m/s^2} \)
Now, use the acceleration to find the speed after \(10 \, \mathrm{s}\):
\( v = at \)
\( v = 4 \times 10 \)
\( v = 40 \, \mathrm{m/s} \)
So, after \(10 \, \mathrm{s}\), the speed of the rocket is \(40 \, \mathrm{m/s}\), and the acceleration during the first \(10 \, \mathrm{s}\) is \(4 \, \mathrm{m/s^2}\).
(ii)When the rocket’s fuel stops burning, it experiences free fall under gravity. We can use the kinematic equation for final velocity (\(v^2 = u^2 + 2gh\)), where \(u\) is the initial velocity after burnout, \(v\) is the final velocity (which is \(0\) at the highest point), \(g\) is the acceleration due to gravity, and \(h\) is the maximum height.
\( 0 = v^2 – 2gh \)
\( 0 = (40)^2 – 2 \times 9.8 \times h \)
\( h = \frac{(40)^2}{2 \times 9.8} \)
\( h \approx 81.63 \, \mathrm{m} \)
So, the maximum height above ground level reached by the rocket is approximately \(81.63 \, \mathrm{m}\).
(iii)We can consider two methods to find the total time of flight:
Method 1: Separate Ascent and Descent Times
– The ascent time (\(t_1\)) can be found using the equation \(0 = v – gt_1\).
– The descent time (\(t_2\)) can be found using the equation \(h = \frac{1}{2}gt_2^2\).
\( t_1 = \frac{v}{g} = \frac{40}{9.8} \approx 4.08 \, \mathrm{s} \)
\( t_2 = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 200}{9.8}} \approx 7.48 \, \mathrm{s} \)
Total time \(= t_1 + t_2 \approx 11.56 \, \mathrm{s}\)
Method 2: Quadratic Equation*
– Use the kinematic equation \(s = ut + \frac{1}{2}at^2\) for descent with \(s = -200\) (negative because it’s downward).
\( -200 = 40t_3 – \frac{1}{2}gt_3^2 \)
\( t_3 = \frac{-v \pm \sqrt{v^2 – 2g(-s)}}{g} \)
\( t_3 \approx \frac{-40 \pm \sqrt{40^2 – 2 \times 9.8 \times (-200)}}{9.8} \)
This gives two possible solutions, but we choose the positive root:
\( t_3 \approx 11.48 \, \mathrm{s} \)
The total time of flight, which is approximately \(11.48 \, \mathrm{s}\).
Question
A particle P moves in a straight line starting from a point O and comes to rest 35 s later. At time ts after leaving O, the velocity v \(ms^{-1}\) of P is given by
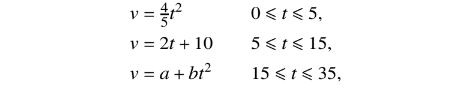
where a and b are constants such that a > 0 and b < 0.
(i) Show that the values of a and b are 49 and −0.04 respectively.
(ii) Sketch the velocity-time graph.
(iii) Find the total distance travelled by P during the 35 s.
Answer/Explanation
Question
A racing car is moving in a straight line. The acceleration\( am s^{-1}\) at time ts after the car starts from rest is given by
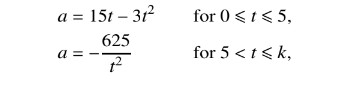
where k is a constant.
(i) Find the maximum acceleration of the car in the first five seconds of its motion.
(ii) Find the distance of the car from its starting point when t = 5.
(iii) The car comes to rest when t = k. Find the value of k.
▶️Answer/Explanation
(i)The given acceleration function is \(a(t) = 15t – 3t^2\) for \(0 \leq t \leq 5\). To find the maximum acceleration, we need to find the critical points by setting the derivative of \(a(t)\) equal to zero:
\(a'(t) = 15 – 6t = 0\)
Solving for \(t\), we get \(t = 2.5\).
To check if this is a maximum, we can look at the second derivative:
\(a”(t) = -6\)
Since the second derivative is negative, \(t = 2.5\) corresponds to a maximum.
Now, we can find the maximum acceleration:
\(a(2.5) = 15 \times 2.5 – 3 \times (2.5)^2 = 18.75 \, \text{m/s}^2\)
(ii) The velocity function is obtained by integrating the acceleration function:
\(v(t) = \int a(t) \, dt = \int (15t – 3t^2) \, dt = \frac{15}{2}t^2 – \frac{1}{4}t^3 + C_1\)
Applying the initial condition \(v(0) = 0\) (as the car starts from rest), we find \(C_1 = 0\).
So, \(v(t) = \frac{15}{2}t^2 – \frac{1}{4}t^3\).
Now, to find the distance traveled, integrate the velocity function:
\(s(t) = \int v(t) \, dt = \int \left(\frac{15}{2}t^2 – \frac{1}{4}t^3\right) \, dt = \frac{5}{2}t^3 – \frac{1}{4}t^4 + C_2\)
Applying the initial condition \(s(0) = 0\), we find \(C_2 = 0\). Therefore, \(s(t) = \frac{5}{2}t^3 – \frac{1}{4}t^4\).
Now, plug in \(t = 5\) to find the distance at \(t = 5\):
\(s(5) = \frac{5}{2}(5)^3 – \frac{1}{4}(5)^4 = \frac{625}{4}\)
So, the distance of the car from its starting point when \(t = 5\) is \(\frac{625}{4} \, \text{meters}\).
(iii) The car comes to rest when the velocity is \(0\).
The velocity function is \(v(t) = \frac{15}{2}t^2 – \frac{1}{4}t^3\).
Set \(v(k) = 0\):
\(v(5) = \frac{15}{2}(5)^2 – \frac{1}{4}(5)^3 = \frac{625}{2} – 125 = -62.5 \, \text{m/s}\)
Now, set \(v(k) = 0\):
\(\frac{625}{k} – 62.5 = 0\)
\(\frac{625}{k} = 62.5\)
\(k = 10\)
So, the correct value of \(k\) is indeed \(10\) seconds.
The car comes to rest at \(t = 10\) seconds.
Question
A particle P is projected vertically upwards from a point O. When the particle is at a height of 0.5 m, its speed is\( 6 ms^{-1}\) . Find
(i) the greatest height reached by the particle above O,
(ii) the time after projection at which the particle returns to O.
▶️Answer/Explanation
(i) The equation of motion for the upward motion of the particle is given by the kinematic equation:
\(v^2 = u^2 – 2gs\)
where:
– \(v\) is the final velocity (\(0 \, \text{m/s}\) at the top),
– \(u\) is the initial velocity (\(6 \, \text{m/s}\)),
– \(g\) is the acceleration due to gravity (\(9.8 \, \text{m/s}^2\)),
– \(s\) is the displacement (which we want to find).
Setting \(v^2\) to \(0\) at the top of the motion, we have:
\(0 = 6^2 – 2 \times 9.8 \times s\)
\(s = \frac{6^2}{2 \times 9.8} = \frac{36}{19.6} = 1.84 \, \text{m}\)
The total height is twice this value since the particle goes up and comes back down:
\( \text{Total Height} = 2 \times 1.84 = 2.3 \, \text{m}\)
(ii) The upward motion of the particle is described by the equation:
\(v^2 = u^2 – 2gs\)
Setting \(v = 0\) (at the top) and rearranging, we get:
\(u^2 = 2gs\)
\(u^2 = 2 \times 9.8 \times 0.5\)
Solving for \(u^2\):
\(u^2 = 46\)
Now, for the downward motion, we use the equation:
\(s = ut + \frac{1}{2}gt^2\)
Since the particle starts from rest at the top, \(u = 0\) and the equation simplifies to:
\(s = \frac{1}{2}gt^2\)
\(2.3 = \frac{1}{2} \times 9.8 \times t^2\)
\(t^2 = \frac{2.3 \times 2}{9.8} \Rightarrow t \approx 0.678 \, \text{s}\)
The total time of flight is then \(2 \times 0.678 = 1.36 \, \text{s}\).
Question
A particle of mass 0.1 kg is released from rest on a rough plane inclined at 20Å to the horizontal. It is given that, 5 seconds after release, the particle has a speed of \(2 ms^{-1}\)
(i) Find the acceleration of the particle and hence show that the magnitude of the frictional force
acting on the particle is 0.302 N, correct to 3 significant figures.
(ii) Find the coefficient of friction between the particle and the plane.
▶️Answer/Explanation
(i) Using kinematic equation
\(2 = 5a \rightarrow a = 0.4 \, \text{m/s}^2\)
Now, to find the frictional force (\(F\)), you applied Newton’s second law along the incline, considering the force components parallel to the incline:
\(0.1 \cdot g \cdot \sin(20^\circ) – F = 0.1 \cdot 0.4\)
Here:
– \(0.1\) is the mass of the particle (\(m\)),
– \(g\) is the acceleration due to gravity (\(9.8 \, \text{m/s}^2\)),
– \(20^\circ\) is the angle of the incline,
– \(F\) is the frictional force,
– \(0.1 \cdot a\) is the component of the gravitational force parallel to the incline.
\(F = 0.1 \cdot g \cdot \sin(20^\circ) – 0.1 \cdot 0.4 = 0.302 \, \text{N}\)
(ii)To find the coefficient of friction (\(\mu\)), you considered the relationship between the frictional force (\(F\)) and the normal force (\(N\)):
\(N = 0.1 \cdot g \cdot \cos(20^\circ)\)
\(\mu = \frac{F}{N} = \frac{0.302}{0.9397} \approx 0.321\)
Question
A particle P moves in a straight line. The velocity v m s−1 at time t s is given by
v = 5t(t − 2) for 0 ≤ t ≤ 4,
v = k for 4 ≤ t ≤ 14,
v = 68 − 2t for 14 ≤ t ≤ 20
where k is a constant.
(i) Find k.
(ii) Sketch the velocity-time graph for 0 ≤ t ≤ 20.
(iii) Find the set of values of t for which the acceleration of P is positive.
(iv) Find the total distance travelled by P in the interval 0 ≤ t ≤ 20.
▶️Answer/Explanation
(i) Finding \( k \)
To find the constant \( k \), we ensure the continuity of the velocity function at \( t = 4 \). Thus, we equate the velocity at \( t = 4 \) for the first equation to \( k \):
\( V = 5 \cdot 4 \cdot (4 – 2) = 40 \)
Therefore, \( k = 40 \, \mathrm{m\,s^{-1}} \).
(ii) Sketching the Velocity-Time Graph
The velocity-time graph for \( 0 \leq t \leq 20 \) can be sketched based on the given equations:
1. For \( 0 \leq t \leq 4 \), \( V = 5t(t – 2) \).
2. For \( 4 \leq t \leq 14 \), \( V = 40 \).
3. For \( 14 \leq t \leq 20 \), \( V = 68 – 2t \).
(iii) Finding Values of \( t \) for Positive Acceleration
The acceleration is the derivative of the velocity function. We need to find the intervals where the derivative is positive.
1. For \( 0 \leq t \leq 4 \), the acceleration is the derivative of \( 5t(t – 2) \).
2. For \( 4 \leq t \leq 14 \), the acceleration is zero since the velocity is constant.
3. For \( 14 \leq t \leq 20 \), the acceleration is the derivative of \( 68 – 2t \).
The acceleration expressions are as follows:
1. For \( 0 \leq t \leq 4 \), the acceleration is \( 10t – 10 \).
2. For \( 14 \leq t \leq 20 \), the acceleration is \( -2 \).
To find when the acceleration is positive, we analyze these expressions:
– For \( 0 \leq t \leq 4 \), \( 10t – 10 > 0 \) implies \( t > 1 \). Therefore, acceleration is positive for \( 1 < t \leq 4 \).
– For \( 14 \leq t \leq 20 \), the acceleration is a constant \( -2 \), which is negative. So, there is no positive acceleration in this interval.
(iv) The total distance travelled by \( P \) in the interval \( 0 \leq t \leq 20 \) is \( 644 \) meters.
– Integral of \( |5t^2 – 10t| \) from \( 0 \) to \( 2 \):
\( A = \left[\frac{5}{3} t^3 – 5 t^2\right]_0^2 = \left(\frac{5}{3} \cdot 2^3 – 5 \cdot 2^2\right) – \left(\frac{5}{3} \cdot 0^3 – 5 \cdot 0^2\right) \)
– Integral of \( 5t^2 – 10t \) from \( 2 \) to \( 4 \):
\( B = \left[\frac{5}{3} t^3 – 5 t^2\right]_2^4 = \left(\frac{5}{3} \cdot 4^3 – 5 \cdot 4^2\right) – \left(\frac{5}{3} \cdot 2^3 – 5 \cdot 2^2\right) \)
– Distance from \( 4 \) to \( 14 \) and \( 14 \) to \( 20 \):
\( C = (40 \times 10) + 0.5 \times (40 + 28) \times 6 \)
Then, combining these parts:
\( -A + B + C = \left[ \frac{20}{3} + \frac{100}{3} + 400 + 204 \right] \)
Hence total distance travelled is 644m.
Question
A uniform lamina is made by joining a rectangle ABCD, in which AB = CD = 0.56 m and BC = AD = 2 m, and a square EFGA of side 1.2 m. The vertex E of the square lies on the edge AD of the rectangle (see diagram). The centre of mass of the lamina is a distance h m from BC and a distance v m from BAG.
(i) Find the value of h and show that v = h.
The lamina is freely suspended at the point B and hangs in equilibrium.
(ii) State the angle which the edge BC makes with the horizontal.
Instead, the lamina is now freely suspended at the point F and hangs in equilibrium.
(iii) Calculate the angle between FG and the vertical.
Answer/Explanation
Ans:

Question
Two particles A and B, of masses 0.8 kg and 0.2 kg respectively, are connected by a light inextensible string. Particle A is placed on a horizontal surface. The string passes over a small smooth pulley P fixed at the edge of the surface, and B hangs freely. The horizontal section of the string, AP, is of length 2.5 m. The particles are released from rest with both sections of the string taut.
(i) Given that the surface is smooth, find the time taken for A to reach the pulley.
(ii) Given instead that the surface is rough and the coefficient of friction between A and the surface is 0.1, find the speed of A immediately before it reaches the pulley.
▶️Answer/Explanation
(i) We are calculating the time taken for particle A to reach the pulley.
Determining the Forces
Forces on Particle B:
– Weight \( W_B = m_B \times g = 0.2 \times 9.81 \) N
Forces on Particle A:
– No frictional force (smooth surface)
Apply Newton’s Second Law
– For Particle B:
\( 0.2 \times g – T = 0.2 \times a \)
\( 0.2 \times 9.81 – T = 0.2 \times a \)
\( 1.962 – T = 0.2 \times a \) (Equation 1)
– For Particle A:
\(T = 0.8 \times a \) (Equation 2)
Solve for Acceleration (a)
– Substituting Equation 2 in Equation 1:
\( 1.962 – 0.8 \times a = 0.2 \times a \)
\( 1.962 = a \times (0.2 + 0.8) \)
\( 1.962 = a \times 1 \)
\( a = 1.962 \, \text{m/s}^2 \)
Calculating Time (t)
– Using the equation of motion \( s = ut + \frac{1}{2}at^2 \)
\( 2.5 = 0 \times t + \frac{1}{2} \times 1.962 \times t^2 \)
\( 2.5 = 0.981 \times t^2 \)
\( t^2 = \frac{2.5}{0.981} \)
\( t^2 \approx 2.5494 \)
\( t \approx \sqrt{2.5494} \)
\(t=1.596\)
The time \( t \) taken for particle A to reach the pulley is approximately \( 1.596 \, \text{s} \).
(ii)Calculating Frictional Force on A:
\( f = \mu \times m \times g \)
\( f = 0.1 \times 0.8 \times 9.81 \)
\( f = 0.7848 \, \text{N} \)
Forces on Particle B:
Weight of B \( = 0.2 \times 9.81 \) N
Forces on Particle A:
Frictional force \( = 0.7848 \, \text{N} \)
Applying Newton’s Second Law:
For B: \( 0.2 \times 9.81 – T = 0.2 \times a \) (Equation 1)
For A: \( T – 0.7848 = 0.8 \times a \) (Equation 2)
Solving for Acceleration \( a \):
\( 0.2 \times 9.81 – T = 0.2 \times a \)
\( T – 0.7848 = 0.8 \times a \)
Solving these gives \( a = 1.177 \, \text{m/s}^2 \)
Calculating Speed of A just before it reaches the pulley:
Using \( v^2 = u^2 + 2as \)
\( v^2 = 0 + 2 \times 1.177 \times 2.5 \)
\( v^2 = 5.885 \)
\( v = \sqrt{5.885} \approx 2.426 \, \text{m/s} \)
Question
A car of mass 1200 kg is pulling a trailer of mass 800 kg up a hill inclined at an angle ! to the horizontal, where sin α = 0.1. The system of the car and the trailer is modelled as two particles connected by a light inextensible cable. The driving force of the car’s engine is 2500 N and the resistances to the car and trailer are 100 N and 150 N respectively.
(i) Find the acceleration of the system and the tension in the cable.
(ii) When the car and trailer are travelling at a speed of 30 m s−1, the driving force becomes zero. The cable remains taut. Find the time, in seconds, before the system comes to rest.
▶️Answer/Explanation
(i) Forces Acting on the System:
The total mass of the system (car + trailer) is \(1200 \, \text{kg} + 800 \, \text{kg} = 2000 \, \text{kg}\).
The driving force is \(2500 \, \text{N}\).
The resistances are \(100 \, \text{N}\) for the car and \(150 \, \text{N}\) for the trailer, totaling \(250 \, \text{N}\).
The component of the gravitational force acting along the incline is \(mg\sin(\alpha)\), where \(m\) is the total mass and \(g\) is the acceleration due to gravity (\(9.8 \, \text{m/s}^2\)).
Calculating Net Force:**
Net force = Driving force – Resistance – Gravitational force component
Gravitational force component
= \(2000 \times 9.8 \times 0.1\) (since \(\sin(\alpha) = 0.1\))
=\( 2000 \times 9.8 \times 0.1 = 1960 \, \text{N} \)
Net force = \(2500 – 250 – 2000 \times 9.8 \times 0.1\)
=\( F_{\text{net}} = 2500 – 250 – 1960 = 290 \, \text{N} \)
Using Newton’s second law, \( F = ma \)
Acceleration \( a = \frac{F}{m} \)
\( a = \frac{F_{\text{net}}}{m} = \frac{290}{2000} = 0.145 \, \text{m/s}^2 \)
Tension in the Cable:
The mass of the trailer is \(800 \, \text{kg}\).
Its gravitational force component is \(800 \times 9.8 \times 0.1\).
Tension = \(800 \times a + 800 \times 9.8 \times 0.1 + 150\)
\( \text{Tension} = 800 \times 0.145 + 800 \times 9.8 \times 0.1 + 150 \)
\( \text{Tension} = 116 + 784 + 150 \)
\( \text{Tension} = 1050 \, \text{N} \)
(ii) Initial Velocity (u)=\(30 \, \text{m/s}\)
Final Velocity (v)=\(0 \, \text{m/s}\) (since it comes to rest)
Acceleration:Now the only forces acting are resistance and gravity. Thus, the acceleration is in the opposite direction.
Net force \(= -250 – 2000 \times 9.8 \times 0.1\) (negative because it’s decelerating)
\( a = \frac{F}{m} \)
Deceleration:
\( a = \frac{-250 – 2000 \times 9.8 \times 0.1}{2000} \)
\( a = \frac{-250 – 1960}{2000} \)
\( a = -1.105 \, \text{m/s}^2 \)
Using the Equation of Motion \( v = u + at \):
\( 0 = 30 – 1.105 \times t \)
\( t = \frac{30}{1.105} \)
\( t \approx 27.15 \, \text{seconds} \)
So, the system will take approximately 27.15 seconds to come to rest.
Question
A cyclist starts from rest at point A and moves in a straight line with acceleration 0.5 m s−2 for a distance of 36 m. The cyclist then travels at constant speed for 25 s before slowing down, with constant deceleration, to come to rest at point B. The distance AB is 210 m.
(i) Find the total time that the cyclist takes to travel from A to B.
24 s after the cyclist leaves point A, a car starts from rest from point A, with constant acceleration 4 m s−2, towards B. It is given that the car overtakes the cyclist while the cyclist is moving with constant speed.
(ii) Find the time that it takes from when the cyclist starts until the car overtakes her.
▶️Answer/Explanation
(i) First Phase (Acceleration):
Acceleration \(a = 0.5 \, \text{m/s}^2\)
Distance \(s = 36 \, \text{m}\)
Using the formula \(s = \frac{1}{2}at^2\) to find the time \(t\) during acceleration.
\( 36 = \frac{1}{2} \times 0.5 \times t^2 \)
\( t^2 = \frac{36 \times 2}{0.5} \)
\( t^2 = 144 \)
\( t = 12 \, \text{s} \)
Second Phase (Constant Speed)
Time \(t = 25 \, \text{s}\) (given)
Third Phase (Deceleration to Stop)
We know the total distance \(AB = 210 \, \text{m}\) and distance covered in phases 1 and 2.
We can find the distance covered during deceleration and then use kinematic equations to find the time for this phase.
Total Distance for Phase 3 (Deceleration):
Total distance = Distance in Phase 1 + Distance in Phase 2 + Distance in Phase 3
Distance in Phase 3 = \(210 \, \text{m} – (36 \, \text{m} + \text{Distance in Phase 2})\)
Phase 2 Distance = Speed (at end of Phase 1) \(\times\) Time
\( \text{Speed at end of Phase 1} = 0.5 \times 12 = 6 \, \text{m/s} \)
\( \text{Distance in Phase 2} = 6 \times 25 = 150 \, \text{m} \)
Distance in Phase 3 = \(210 – (36 + 150) = 24 \, \text{m}\)
Now, we use the equation \( s = ut + \frac{1}{2}at^2 \) for deceleration. Here, \(u = 6 \, \text{m/s}\) (speed at the end of Phase 1), \(s = 24 \, \text{m}\), and \(a\) is the deceleration which we don’t know.
However, we can use the fact that the cyclist comes to rest to find \(a\), and then solve for \(t\).
Let’s calculate the deceleration first and then the time for Phase 3.
Using \( v^2 = u^2 + 2as \), where \(v = 0 \, \text{m/s}\) (final velocity),
\( 0 = 6^2 + 2 \times a \times 24 \)
\( 36 = -48a \)
\( a = -\frac{36}{48} = -0.75 \, \text{m/s}^2 \)
Now, using \( v = u + at \),
\( 0 = 6 – 0.75 \times t \)
\( t = \frac{6}{0.75} \)
\( t = 8 \, \text{s} \)
Total Time:
Total time = Time in Phase 1 + Time in Phase 2 + Time in Phase 3
\( \text{Total time} = 12 \, \text{s} + 25 \, \text{s} + 8 \, \text{s} \)
\( \text{Total time} = 45 \, \text{s} \)
(ii) Cyclist’s Head Start:
The cyclist has a 24-second head start.
Cyclist’s Position at 24 Seconds:
The cyclist has finished Phase 1 (12 seconds) and is 12 seconds into Phase 2.
Distance Covered by Cyclist in 24 Seconds:
Distance in Phase 1 = 36 m
Distance in 12 seconds of Phase 2 = \(6 \times 12 = 72 \, \text{m}\)
Total = \(36 + 72 = 108 \, \text{m}\)
Car’s Journey:**
The car starts from rest and accelerates at \(4 \, \text{m/s}^2\).
We need to find the time it takes for the car to cover the same distance as the cyclist, considering the cyclist’s constant speed phase.
For the car,
\( s = \frac{1}{2}at^2 \)
\( 108 = \frac{1}{2} \times 4 \times t^2 \)
\( t^2 = \frac{108 \times 2}{4} \)
\( t^2 = 54 \)
\( t = \sqrt{54} \approx 7.35 \, \text{s} \)
So, the car takes approximately 7.35 seconds to reach the cyclist’s position after it starts.
Total Time Until Overtaking
Total time = Cyclist’s head start + Time for car to reach cyclist
\( \text{Total time} = 24 \, \text{s} + 7.35 \, \text{s} \)
\( \text{Total time} \approx 31.35 \, \text{s} \)
Thus, it takes approximately 31.35 seconds from the time the cyclist starts until the car overtakes her.
Question
A particle P moves in a straight line, starting from a point O. The velocity of P, measured in m s−1, at time t s after leaving O is given by
v = 0.6t − 0.03t2.
(i) Verify that, when t = 5, the particle is 6.25 m from O. Find the acceleration of the particle at this time.
(ii) Find the values of t at which the particle is travelling at half of its maximum velocity.
▶️Answer/Explanation
(i) Distance from O and Acceleration at \( t = 5 \, \text{s} \)
Velocity Function: \[ v = 0.6t – 0.03t^2 \]
Distance Calculation:
Distance traveled by the particle can be found by integrating the velocity function with respect to time.
\( \text{Distance} = \int v \, dt = \int (0.6t – 0.03t^2) \, dt \)
\( \text{Distance} = \int_0^5 (0.6t – 0.03t^2) \, dt \)
\( \text{Distance} = \left[ 0.3t^2 – 0.01t^3 \right]_0^5 \)
\( \text{Distance} = \left( 0.3 \times 5^2 – 0.01 \times 5^3 \right) – \left( 0.3 \times 0^2 – 0.01 \times 0^3 \right) \]
\( \text{Distance} = (0.3 \times 25 – 0.01 \times 125) \)
\( \text{Distance} = (7.5 – 1.25) \)
\( \text{Distance} = 6.25 \, \text{m} \)
Acceleration is the derivative of the velocity function with respect to time.
\( \text{Acceleration} = \frac{dv}{dt} \)
\( \text{Acceleration} = \frac{d(0.6t – 0.03t^2)}{dt} \)
\( \text{Acceleration} = 0.6 – 0.06t \)
\( \text{Acceleration at } t = 5 \, \text{s} = 0.6 – 0.06 \times 5 \)
\( \text{Acceleration at } t = 5 \, \text{s} = 0.6 – 0.3 \)
\( \text{Acceleration at } t = 5 \, \text{s} = 0.3 \, \text{m/s}^2 \)
(ii)The maximum velocity occurs when the derivative of the velocity function is zero (i.e., acceleration is zero).
Set the acceleration formula equal to zero and solve for \( t \).
Set acceleration to zero:
\( 0.6 – 0.06t = 0 \)
\( 0.06t = 0.6 \)
\( t = \frac{0.6}{0.06} \)
\( t = 10 \, \text{s} \)
Now, we find the maximum velocity at \( t = 10 \, \text{s} \):
\( v_{\text{max}} = 0.6 \times 10 – 0.03 \times 10^2 \)
\( v_{\text{max}} = 6 – 3 \)
\( v_{\text{max}} = 3 \, \text{m/s} \)
Half of the maximum velocity is \( \frac{3}{2} = 1.5 \, \text{m/s} \).
Set the velocity equation to 1.5 and solve for \( t \)
\( 0.6t – 0.03t^2 = 1.5 \)
\( 0.03t^2 – 0.6t + 1.5 = 0 \)
This is a quadratic equation in the form \( at^2 + bt + c = 0 \). We solve for \( t \) using the quadratic formula:
\( t = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \)
Where \( a = 0.03 \), \( b = -0.6 \), and \( c = 1.5 \).
\( t = \frac{-(-0.6) \pm \sqrt{(-0.6)^2 – 4 \times 0.03 \times 1.5}}{2 \times 0.03} \)
\( t = \frac{0.6 \pm \sqrt{0.36 – 0.18}}{0.06} \)
\( t = \frac{0.6 \pm \sqrt{0.18}}{0.06} \)
Calculate the two possible values for \( t \):
\[ t_1 = \frac{0.6 + \sqrt{0.18}}{0.06} \]=17.07s
\[ t_2 = \frac{0.6 – \sqrt{0.18}}{0.06} \]=2.92s
Question
A particle of mass 0.5 kg starts from rest and slides down a line of greatest slope of a smooth plane. The plane is inclined at an angle of 30° to the horizontal.
(i) Find the time taken for the particle to reach a speed of 2.5 m s−1.
When the particle has travelled 3 m down the slope from its starting point, it reaches rough horizontal ground at the bottom of the slope. The frictional force acting on the particle is 1 N.
(ii) Find the distance that the particle travels along the ground before it comes to rest.
▶️Answer/Explanation
(i) Forces Acting on the Particle:
Only gravity is acting along the slope since the plane is smooth.
The component of gravitational force along the slope is \(mg\sin\theta\), where \(m\) is mass, \(g\) is the acceleration due to gravity (\(9.8 \, \text{m/s}^2\)), and \(\theta\) is the angle of incline (\(30^\circ\)).
Since there are no other forces acting along the slope, the acceleration of the particle is \(g\sin\theta\).
\( \text{Acceleration} = g\sin\theta = 9.8 \times \sin(30^\circ) \)
\( \text{Acceleration} = 9.8 \times 0.5 = 4.9 \, \text{m/s}^2 \)
Using the Equation of Motion:
The initial velocity \(u = 0 \, \text{m/s}\) (since it starts from rest), and the final velocity \(v = 2.5 \, \text{m/s}\).
We use \( v = u + at \) to solve for time \(t\).
Now, using \( v = u + at \),
\( 2.5 = 0 + 4.9 \times t \)
\( t = \frac{2.5}{4.9} \)
\( t \approx 0.51 \, \text{s} \)
(ii) Initial Velocity:
The particle’s velocity at the end of the slope can be calculated using the equation \( v^2 = u^2 + 2as \), where \(s\) is the distance traveled down the slope (3 m).
We already calculated the acceleration down the slope as \(4.9 \, \text{m/s}^2\).
\( v^2 = u^2 + 2as \)
\( v^2 = 0 + 2 \times 4.9 \times 3 \)
\( v^2 = 29.4 \)
\( v = \sqrt{29.4} \)
\( v \approx 5.42 \, \text{m/s} \)
Deceleration Due to Friction:
Frictional force \(F = 1 \, \text{N}\).
Deceleration \(a = \frac{F}{m}\).
\( a = \frac{F}{m} = \frac{1}{0.5} = 2 \, \text{m/s}^2 \)
Distance Traveled Along the Ground:
Using the equation \( v^2 = u^2 + 2as \) again, but this time to calculate the distance \(s\) along the ground, with final velocity \(v = 0 \, \text{m/s}\) (comes to rest).
\( 0 = v^2 – 2as \)
\( s = \frac{v^2}{2a} = \frac{5.42^2}{2 \times 2} \)
\( s \approx \frac{29.4}{4} \)
\( s \approx 7.35 \, \text{m} \)
Therefore, the particle travels approximately 7.35 meters along the ground before coming to rest.
Question
Two particles A and B start to move at the same instant from a point O. The particles move in the same direction along the same straight line. The acceleration of A at time t s after starting to move is am s−2 , where a = 0.05 − 0.0002t.
(i) Find A’s velocity when t = 200 and when t = 500.
B moves with constant acceleration for the first 200 s and has the same velocity as A when t = 200. B moves with constant retardation from t = 200 to t = 500 and has the same velocity as A when t = 500.
(ii) Find the distance between A and B when t = 500.
▶️Answer/Explanation
(i)To find the velocity of particle A at specific times, we need to integrate the acceleration function over time.
Acceleration Function for A:\( a = 0.05 – 0.0002t \)
Velocity is the integral of acceleration with respect to time.
The particle starts from rest, so initial velocity \( u = 0 \).
For \( t = 200 \) and \( t = 500 \), the velocity \( v \) is calculated as follows:
\( v = \int_0^t (0.05 – 0.0002t) \, dt \)
Let’s calculate it for \( t = 200 \) and \( t = 500 \) separately.
For \( t = 200 \) seconds:
\( v_{200} = \int_0^{200} (0.05 – 0.0002t) \, dt \)
For \( t = 500 \) seconds:
\( v_{500} = \int_0^{500} (0.05 – 0.0002t) \, dt \)
For \( t = 200 \):
\( v_{200} = \left[ 0.05t – 0.0001t^2 \right]_0^{200} \)
\( v_{200} = \left( 0.05 \times 200 – 0.0001 \times 200^2 \right) – \left( 0.05 \times 0 – 0.0001 \times 0^2 \right) \)
\( v_{200} = 10 – 4 = 6 \, \text{m/s} \)
For \( t = 500 \):
\( v_{500} = \left[ 0.05t – 0.0001t^2 \right]_0^{500} \)
\( v_{500} = \left( 0.05 \times 500 – 0.0001 \times 500^2 \right) – \left( 0.05 \times 0 – 0.0001 \times 0^2 \right) \)
\( v_{500} = 25 – 25 = 0 \, \text{m/s} \)
(ii) Distance Between A and B when \( t = 500 \)
Distance Covered by A:
As calculated, we integrate A’s velocity function from 0 to 500 seconds to find the distance covered by A.
\( \text{Distance}_A = \int_0^{500} (0.05t – 0.0001t^2) \, dt \)
\( \text{Distance}_A = \left[ \frac{0.05t^2}{2} – \frac{0.0001t^3}{3} \right]_0^{500} \)
\( \text{Distance}_A = \left[ \frac{0.05 \times 500^2}{2} – \frac{0.0001 \times 500^3}{3} \right] – \left[ \frac{0.05 \times 0^2}{2} – \frac{0.0001 \times 0^3}{3} \right] \)
\( \text{Distance}_A = \left[ 0.025 \times 250000 – \frac{0.0001 \times 125000000}{3} \right] \)
\( \text{Distance}_A = \left[ 6250 – \frac{12500}{3} \right] \)
\( \text{Distance}_A = 6250 – 4166.67 \)
\( \text{Distance}_A = 2083.33 \, \text{m} \)
Distance Between A and B:
\( \text{Distance between A and B} = \text{Distance}_A – \text{Distance}_B \)
\( = 2083.33 \, \text{m} – 1500 \, \text{m} \)
\( = 583.33 \, \text{m} \)
So, the distance between A and B when \( t = 500 \) is approximately 583.33 meters.
Question
A particle of mass 3 kg falls from rest at a point 5 m above the surface of a liquid which is in a container. There is no instantaneous change in speed of the particle as it enters the liquid. The depth of the liquid in the container is 4 m. The downward acceleration of the particle while it is moving in the liquid is \(5.5 ms^{-2}\)
.(i) Find the resistance to motion of the particle while it is moving in the liquid.
(ii) Sketch the velocity-time graph for the motion of the particle, from the time it starts to move until the time it reaches the bottom of the container. Show on your sketch the velocity and the time when the particle enters the liquid, and when the particle reaches the bottom of the container.
▶️Answer/Explanation
(i) – Finding the Resistance to Motion in the L
To find the resistance to the motion of the particle in the liquid, we need to analyze the forces acting on the particle while it’s in the liquid.
Forces Acting on the Particle in the Liquid:
The downward force is the weight of the particle, \( mg \), where \( m = 3 \, \text{kg} \) and \( g = 9.8 \, \text{m/s}^2 \).
The upward force is the resistance to motion, which we need to calculate.
The net force acting on the particle is \( ma \), where \( a = 5.5 \, \text{m/s}^2 \).
Net Force in the Liquid:
\( F_{\text{net}} = ma = 3 \times 5.5 \, \text{N} \)
\( F_{\text{net}} = ma = 3 \times 5.5 \)
\( F_{\text{net}} = 16.5 \, \text{N} \)
The net force is the difference between the weight and the resistance.
\( F_{\text{net}} = mg – \text{Resistance} \)
Now, using \( F_{\text{net}} = mg – \text{Resistance} \),
\( 16.5 = 3 \times 9.8 – \text{Resistance} \)
\( \text{Resistance} = 3 \times 9.8 – 16.5 \)
\( \text{Resistance} = 29.4 – 16.5 \)
\( \text{Resistance} = 12.9 \, \text{N} \)
(ii) Velocity When Entering the Liquid:
Calculated the velocity upon entering the liquid using \( v^2 = 2gs \), where \( s = 5 \, \text{m} \) and \( g = 9.8 \, \text{m/s}^2 \):
\( v_s^2 = 2 \times 9.8 \times 5 \)
\( v_s^2 = 98 \)
\( v_s = \sqrt{98} \)
\( v_s \approx 9.9 \, \text{m/s} \)
Velocity at the Bottom of the Container:
Calculated the velocity at the bottom using \( v_b^2 = v_s^2 + 2as \), where \( a = 5.5 \, \text{m/s}^2 \) and \( s = 4 \, \text{m} \):
\( v_b^2 = 9.9^2 + 2 \times 5.5 \times 4 \)
\( v_b^2 = 98 + 44 \)
\( v_b^2 = 142 \)
\( v_b = \sqrt{142} \]
\( v_b \approx 11.9 \, \text{m/s} \)
Time to Reach the Surface of the Liquid:
\( v_s = 0 + gt_1 \)
\( 9.9 = 9.8t_1 \)
\( t_1 = \frac{9.9}{9.8} \approx 1 \, \text{s} \)
Time to Reach the Bottom of the Container:
\( v_b = v_s + a(t_2 – t_1) \)
\( 11.9 = 9.9 + 5.5(t_2 – 1) \)
\( 2 = 5.5t_2 – 5.5 \)
\( 7.5 = 5.5t_2 \)
\( t_2 = \frac{7.5}{5.5} \approx 1.36 \, \text{s} \)
Sketch of the Graph:
Phase 1 (Free Fall): A line from \( (0, 0) \) to \( (1 \, \text{s}, 9.9 \, \text{m/s}) \).
Phase 2 (In Liquid): A line starting from \( (1 \, \text{s}, 9.9 \, \text{m/s}) \) and ending at \( (1.36 \, \text{s}, 11.9 \, \text{m/s}) \).
The first segment represents acceleration due to gravity, and the second segment represents the particle’s motion in the liquid with a constant but smaller acceleration. The graph should show a continuous increase in velocity with a change in slope at \( t = 1 \, \text{s} \).
Question
Particles P and Q move on a straight line AOB. The particles leave O simultaneously, with P moving towards A and with Q moving towards B. The initial speed of P is 1.3 \(ms^{-1}\) and its acceleration in the direction OA is 0.1 \(ms^{-2}\) . Q moves with acceleration in the direction OB of 0.016t \(ms^{-2}\) , where t seconds is the time elapsed since the instant that P and Q started to move from O. When t = 20, particle P passes through A and particle Q passes through B.
(i) Given that the speed of Q at B is the same as the speed of P at A, find the speed of Q at time t = 0. [4]
(ii) Find the distance AB.
▶️Answer/Explanation
(i) Given that the speed of Q at B (at \( t = 20 \, \text{s} \)) is the same as the speed of P at A, we can equate their final speeds to find the initial speed of Q.
Final Speed of P at A:
Initial speed of P \( u_P = 1.3 \, \text{m/s} \)
Acceleration of P \( a_P = 0.1 \, \text{m/s}^2 \)
Time \( t = 20 \, \text{s} \)
Final speed \( v_P = u_P + a_P t \)
\( v_P = 1.3 + 0.1 \times 20 \)
\( v_P = 1.3 + 2 \)
\( v_P = 3.3 \, \text{m/s} \)
Final Speed of Q at B:
Let the initial speed of Q be \( u_Q \)
Acceleration of Q \( a_Q = 0.016t \, \text{m/s}^2 \)
Final speed \( v_Q = u_Q + \int_0^{20} a_Q \, dt \)
For Q, \( v_Q \) is calculated by integrating the acceleration over time from 0 to 20 seconds:
\( v_Q = u_Q + \int_0^{20} 0.016t \, dt \)
\( v_Q = u_Q + \left[ 0.008t^2 \right]_0^{20} \)
\( v_Q = u_Q + (0.008 \times 20^2) \)
\( v_Q = u_Q + 3.2 \)
Equating \( v_P \) and \( v_Q \), we can solve for \( u_Q \).
Setting \( v_P \) equal to \( v_Q \):
\( 3.3 = u_Q + 3.2 \)
\( u_Q = 3.3 – 3.2 \)
\( u_Q = 0.1 \, \text{m/s} \)
So, the initial speed of Q at \( t = 0 \) is \( 0.1 \, \text{m/s} \).
(ii) To find the distance AB, we need to calculate the distances AP and OB separately and then add them together. The distances can be found by integrating the velocity functions from \( t = 0 \) to \( t = 20 \) seconds.
Distance AP (for Particle P):**
Distance \( s_P = \int_0^{20} v_P \, dt \)
\( v_P = u_P + a_P t \)
\( s_P = \int_0^{20} (1.3 + 0.1t) \, dt \)
\( s_P = \left[ 1.3t + 0.05t^2 \right]_0^{20} \)
\( s_P = (1.3 \times 20 + 0.05 \times 20^2) \)
\( s_P = 26 + 20 \)
\( s_P = 46 \, \text{m} \)
Distance OB (for Particle Q):
Distance \( s_Q = \int_0^{20} v_Q \, dt \)
\( v_Q = u_Q + \int_0^{t} a_Q \, dt \)
\( s_Q = \int_0^{20} (0.1 + \int_0^{t} 0.016t \, dt) \, dt \)
\( s_Q = \int_0^{20} (0.1 + 0.008t^2) \, dt \)
\( s_Q = \left[ 0.1t + \frac{0.008}{3}t^3 \right]_0^{20} \)
\( s_Q = (0.1 \times 20 + \frac{0.008}{3} \times 20^3) \)
\( s_Q = 2 + \frac{0.008}{3} \times 8000 \)
\( s_Q = 2 + \frac{64}{3} \)
\( s_Q = 2 + 21.33 \)
\( s_Q = 23.33 \, \text{m} \)
Total Distance AB:
\( AB = AP + OB \)
\( AB = 46 \, \text{m} + 23.33 \, \text{m} \)
\( AB = 69.33 \, \text{m} \)
Therefore, the distance AB is approximately \( 69.33 \) meters.
Question
Two cyclists P and Q travel along a straight road ABC, starting simultaneously at A and arriving simultaneously at C. Both cyclists pass through B 400 s after leaving A. Cyclist P starts with speed \(3ms^{-1}\)and increases this speed with constant acceleration 0.005 \(m s^{-2} \)until he reaches B.
(i) Show that the distance AB is 1600 m and find P’s speed at B. Cyclist Q travels from A to B with speed \(v ms^{-1}\) at time t seconds after leaving A, where
v = 0.04t −\( 0.0001t^{2} \)+k, and k is a constant.
(ii) Find the value of k and the maximum speed of Q before he has reached B. Cyclist P travels from B to C, a distance of 1400 m, at the speed he had reached at B. Cyclist Q travels from B to C with constant acceleration a\(m s^{-1}\)
.(iii) Find the time taken for the cyclists to travel from B to C and find the value of a.
▶️Answer/Explanation
(i) Distance AB for Cyclist P:**
Initial speed \( u_P = 3 \, \text{m/s} \)
Acceleration \( a_P = 0.005 \, \text{m/s}^2 \)
Time \( t = 400 \, \text{s} \)
Distance \( s = ut + \frac{1}{2}at^2 \)
\( s_P = 3 \times 400 + \frac{1}{2} \times 0.005 \times 400^2 \)
\( s_P = 1200 + 0.0025 \times 160000 \)
\( s_P = 1200 + 400 \)
\( s_P = 1600 \, \text{m} \]
So, the distance AB is \( 1600 \, \text{m} \).
P’s Speed at B:
\( v_P = u_P + a_Pt \)
\(v_P = 3 + 0.005 \times 400 \)
\( v_P = 3 + 2 \)
\( v_P = 5 \, \text{m/s} \)
(ii)Velocity Function for Q:\( v_Q = 0.04t – 0.0001t^2 + k \)
Velocity of Q at \( t = 400 \, \text{s} \):Equating Q’s velocity at B with P’s velocity at B.
\( v_Q = 0.04 \times 400 – 0.0001 \times 400^2 + k \)
\( 5 = 16 – 16 + k \)
\( k = 5 \, \text{m/s} \)
So, \( k = 5 \, \text{m/s} \).
Maximum Speed of Q:
Maximum speed occurs where the derivative of the velocity function is zero.
\( \frac{dv_Q}{dt} = 0.04 – 0.0002t = 0 \)
\( 0.04 = 0.0002t \)
\( t = \frac{0.04}{0.0002} \)
\( t = 200 \, \text{s} \)
Now calculate the maximum speed:
\( v_{\text{max}} = 0.04 \times 200 – 0.0001 \times 200^2 + 5 \)
\( v_{\text{max}} = 8 – 4 + 5 \)
\( v_{\text{max}} = 9 \, \text{m/s} \)
(iii) Distance BC:
For P, \( s = 1400 \, \text{m} \) and \( v_P = 5 \, \text{m/s} \) (constant).
Time \( t_P = \frac{s}{v} \).
Time for P from B to C:
\( t_P = \frac{1400}{5} \)
\( t_P = 280 \, \text{s} \)
Time for Q from B to C:
Since P and Q arrive at C simultaneously, \( t_Q = t_P = 280 \, \text{s} \).
Using Q’s motion from B to C to find \( a \):
\( 1400 = 9 \times 280 + \frac{1}{2} \times a \times 280^2 \)
\( 1400 = 2520 + 39200a \)
\( 39200a = 1400 – 2520 \)
\( 39200a = -1120 \)
\( a = -\frac{1120}{39200} \)
\( a \approx -0.0286 \, \text{m/s}^2 \)
So, the time taken from B to C is 280 seconds for both cyclists, and the value of \( a \) for Q is approximately \( -0.0286 \, \text{m/s}^2 \).
Question
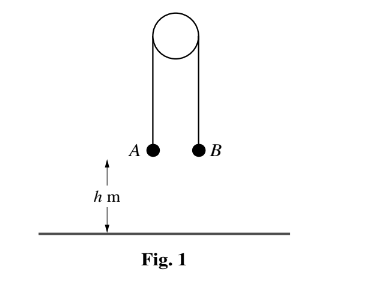
Particles A of mass 0.25 kg and B of mass 0.75 kg are attached to opposite ends of a light inextensible string which passes over a fixed smooth pulley. The system is held at rest with the string taut and its straight parts vertical. Both particles are at a height of h m above the floor (see Fig. 1). The system is released from rest, and 0.6 s later, when both particles are in motion, the string breaks. The particle A does not reach the pulley in the subsequent motion.
(i) Find the acceleration of A and the distance travelled by A before the string breaks.
The velocity-time graph shown in Fig. 2 is for the motion of particle A until it hits the floor. The velocity of A when the string breaks is\( V ms^{-1}\) and T s is the time taken for A to reach its greatest height.
(ii) Find the value of V and the value of T.
(iii) Find the distance travelled by A upwards and the distance travelled by A downwards and hence find h.
▶️Answer/Explanation
(i) System Before the String Breaks:
Mass of A, \( m_A = 0.25 \, \text{kg} \)
Mass of B, \( m_B = 0.75 \, \text{kg} \)
Acceleration due to gravity, \( g = 9.8 \, \text{m/s}^2 \)
\( (0.75 \times 9.8 – 0.25 \times 9.8) = (0.25 + 0.75) \times a \)
\( (7.35 – 2.45) = 1 \times a \)
\( 4.9 = a \)
\( a = 4.9 \, \text{m/s}^2 \)
Forces on A and B:
Force on A = \( m_A g \)
Force on B = \( m_B g \)
Net force = Force on B – Force on A
Acceleration and Tension in the String:
Net force = (Total mass) \(\times\) Acceleration
\( (m_B g – m_A g) = (m_A + m_B) \times a \)
Distance Traveled by A:
\( s = ut + \frac{1}{2}at^2 \)
Given \( u = 0 \, \text{m/s} \) and \( t = 0.6 \, \text{s} \),
\( s = 0 + \frac{1}{2} \times 4.9 \times 0.6^2 \)
\( s = 0.5 \times 4.9 \times 0.36 \)
\( s = 2.45 \times 0.36 \)
\( s = 0.882 \, \text{m} \)
(ii) Velocity V When String Breaks:**
\( v = u + at \)
\( v = 0 + 4.9 \times 0.6 \)
\( V = 4.9 \times 0.6 \)
\( V = 2.94 \, \text{m/s} \)
Time T to Reach Greatest Height
At greatest height, final velocity \( v = 0 \, \text{m/s} \)
Using \( v = u + at \) with \( a = -g \) (deceleration due to gravity)
\( 0 = 2.94 – 9.8T \)
\( 9.8T = 2.94 \)
\( T = \frac{2.94}{9.8} \)
\( T \approx 0.3 \, \text{s} \)
(iii) Distance Upwards:
Use \( s = ut + \frac{1}{2}at^2 \) with \( u = 2.94 \, \text{m/s} \), \( a = -9.8 \, \text{m/s}^2 \), and \( t = T \)
\( s_{\text{up}} = 2.94 \times 0.3 + \frac{1}{2} \times -9.8 \times 0.3^2 \)
\( s_{\text{up}} = 0.882 – 0.441 \)
\( s_{\text{up}} = 0.441 \, \text{m} \)
Total Time in the Air (From Break to Floor):
\( t_{\text{total}} = T + \text{time falling down} \)
Using \( v = u + gt \) for the downward motion from rest, where \( v = 0 \) at the peak
\( v = 0 + 9.8t \)
\( v \) is the velocity when A hits the ground. We use the energy conservation principle: \( \frac{1}{2}mv^2 = mgh \), where \( h = s_{\text{up}} + \text{distance downwards} \).
Total Distance Traveled by A Downwards:
\( v^2 = 2gh \)
\( 2 \times 9.8 \times h = 9.8 \times (0.441 + s_{\text{down}}) \)
\( 2h = 0.441 + s_{\text{down}} \)
Use \( h = s_{\text{up}} + s_{\text{down}} \)
\( s_{\text{down}} = h – s_{\text{up}} \)
From the energy conservation equation, \( \frac{1}{2} \times 0.25 \times v^2 = 0.25 \times 9.8 \times h \)
Given \( h = 0.882 \, \text{m} \) (from the distance A traveled before the string breaks),
\( 2 \times 0.882 = 0.441 + s_{\text{down}} \)
\( 1.764 = 0.441 + s_{\text{down}} \)
\( s_{\text{down}} = 1.764 – 0.441 \)
\( s_{\text{down}} = 1.323 \, \text{m} \)
So, \( h \) is the sum of \( s_{\text{up}} \) and \( s_{\text{down}} \),
\( h = 0.441 + 1.323 \)
\( h = 1.764 \, \text{m} \)
Therefore, the height \( h \) is approximately \( 1.764 \, \text{m} \).
Question
A particle is projected vertically upwards with speed 9 m s−1 from a point 3.15 m above horizontal ground. The particle moves freely under gravity until it hits the ground. For the particle’s motion from the instant of projection until the particle hits the ground, find the total distance travelled and the total time taken.
▶️Answer/Explanation
Upward Motion
Initial Velocity (u): \( 9 \, \text{m/s} \) (upward)
Acceleration (a):\( -9.8 \, \text{m/s}^2 \) (downward, due to gravity)
Final Velocity (v) at Highest Point: \( 0 \, \text{m/s} \)
Using the kinematic equation \( v^2 = u^2 + 2as \) to find the maximum height (s) reached:
\( 0 = 9^2 + 2 \times (-9.8) \times s \)
\( s = \frac{81}{19.6} \)
\( s \approx 4.13 \, \text{m} \)
Total height from the ground at the peak of the trajectory:
\( h_{\text{peak}} = 4.13 \, \text{m} + 3.15 \, \text{m} \)
\( h_{\text{peak}} = 7.28 \, \text{m} \)
Time taken to reach the highest point, using \( v = u + at \):
\( 0 = 9 – 9.8t \)
\( t = \frac{9}{9.8} \)
\( t \approx 0.92 \, \text{s} \)
Downward Motion
Initial Velocity (u):\( 0 \, \text{m/s} \) (from rest at the highest point)
Acceleration (a): \( 9.8 \, \text{m/s}^2 \) (downward)
Distance (s) to Ground:\( 7.28 \, \text{m} \)
Using \( s = ut + \frac{1}{2}at^2 \) to find the time taken to hit the ground:
\( 7.28 = 0 \times t + \frac{1}{2} \times 9.8 \times t^2 \)
\( 7.28 = 4.9t^2 \)
\( t^2 = \frac{7.28}{4.9} \)
\( t \approx \sqrt{1.49} \)
\( t \approx 1.22 \, \text{s} \)
Total Distance and Total Time
Total Distance Traveled:
Upward: \( 4.13 \, \text{m} \)
Downward: \( 7.28 \, \text{m} \)
Total Distance: \( 4.13 \, \text{m} + 7.28 \, \text{m} = 11.41 \, \text{m} \)
Total Time Taken:
Upward: \( 0.92 \, \text{s} \)
Downward: \( 1.22 \, \text{s} \)
Total Time: \( 0.92 \, \text{s} + 1.22 \, \text{s} = 2.14 \, \text{s} \)
Therefore, the total distance traveled by the particle is approximately \( 11.41 \, \text{m} \), and the total time taken is approximately \( 2.14 \, \text{s} \).
Question
A particle P starts from rest at a point O and moves in a straight line. P has acceleration 0.6t m s−2 at time t seconds after leaving O, until t = 10.
(i) Find the velocity and displacement from O of P when t = 10.
After t = 10, P has acceleration −0.4t m s−2 until it comes to rest at a point A.
(ii) Find the distance OA.
▶️Answer/Explanation
(i) Acceleration Function:\( a = 0.6t \, \text{m/s}^2 \)
Finding Velocity at \( t = 10 \):
Velocity is the integral of acceleration with respect to time.
Since P starts from rest, initial velocity \( u = 0 \).
\( v = \int_0^{10} 0.6t \, dt \)
\( v = \left[ 0.3t^2 \right]_0^{10} \)
\(v = 0.3 \times 10^2 = 30 \, \text{m/s} \)
Displacement is the integral of velocity with respect to time.
\( s = \int_0^{10} v \, dt \)
\( s = \int_0^{10} 0.3t^2 \, dt \)
\( s = \left[ \frac{0.3t^3}{3} \right]_0^{10} \)
\( s = \frac{0.3 \times 10^3}{3} = 100 \, \text{m} \)
(ii) For the second part of the motion, after \( t = 10 \, \text{s} \), particle P has a deceleration of \( -0.4t \, \text{m/s}^2 \). We need to find the additional distance traveled by P from \( t = 10 \) to when it comes to rest.
Initial Conditions at \( t = 10 \, \text{s} \):
Initial Velocity \( u = 30 \, \text{m/s} \) (from part i)
Acceleration \( a = -0.4t \, \text{m/s}^2 \)
The time taken for the particle to come to rest can be found by setting the final velocity to zero in the velocity-time equation \( v = u + at \).
\( 0 = 30 – 4(t – 10) \)
\( 4t – 40 = 30 \)
\( 4t = 70 \)
\( t = 17.5 \, \text{s} \)
So, the particle comes to rest at \( t = 17.5 \, \text{s} \).
The additional distance is the distance traveled from \( t = 10 \) to \( t = 17.5 \). The acceleration function is a function of time, so we integrate the velocity function from \( t = 10 \) to \( t = 17.5 \):
\( s = \int_{10}^{17.5} (30 – 0.4 \times 10 \times (t – 10)) \, dt \)
\( s = \int_{10}^{17.5} (30 – 4t + 40) \, dt \)
\( s = \int_{10}^{17.5} (70 – 4t) \, dt \)
\( s = \left[ 70t – 2t^2 \right]_{10}^{17.5} \)
Calculate this definite integral to find the distance.
\( s = (70 \times 17.5 – 2 \times 17.5^2) – (70 \times 10 – 2 \times 10^2) \)
\( s = (1225 – 612.5) – (700 – 200) \)
\( s = 612.5 – 500 \)
\( s = 112.5 \, \text{m} \)
otal Distance OA:
The total distance OA is the sum of the displacement from \( t = 0 \) to \( t = 10 \) (which was 100 m from part i) and the additional distance from \( t = 10 \) to \( t = 17.5 \):
\( OA = 100 \, \text{m} + 112.5 \, \text{m} \)
\( OA = 212.5 \, \text{m} \)
Therefore, the total distance OA is approximately \( 212.5 \, \text{m} \).
Question
Particles A and B, of masses 0.3 kg and 0.7 kg respectively, are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley. A is held at rest and B hangs freely, with both straight parts of the string vertical and both particles at a height of 0.52 m above the floor (see diagram). A is released and both particles start to move.
(i) Find the tension in the string.
When both particles are moving with speed 1.6 m s−1 the string breaks.
(ii) Find the time taken, from the instant that the string breaks, for A to reach the floor.
▶️Answer/Explanation
(i)When particle A is released, both A and B will start to move due to gravity. The system will accelerate under the influence of the net force caused by the difference in the gravitational forces acting on A and B. We can analyze this using Newton’s second law.
For particle A (of mass 0.3 kg), the forces acting on it are tension (T) upwards and its weight (0.3g) downwards.
For particle B (of mass 0.7 kg), the forces are its weight (0.7g) downwards and tension (T) upwards.
For A:
\( T – 0.3g = 0.3a \)
For B:
\( 0.7g – T = 0.7a \)
We can solve these equations simultaneously to find T and a. Adding both equations gives us the net force acting on the system, which leads to the acceleration:
\( T – 0.3g + 0.7g – T = 0.3a + 0.7a \)
\( 0.4g = a \)
\(a = 0.4 \times 9.8 \)
\( a = 3.92 \, \text{m/s}^2 \)
Now substituting the value of a back into equation (1) or (2), we can solve for T:
\( T – 0.3 \times 9.8 = 0.3 \times 3.92 \)
\( T = 0.3 \times 9.8 + 0.3 \times 3.92 \)
\( T = 2.94 + 1.176 \)
\( T = 4.116 \, \text{N} \)
So, the tension in the string is approximately 4.116 N.
(ii)When the string breaks, particle A will fall freely under gravity. We can use the equations of motion to find the time taken for A to reach the floor.
The initial velocity of A when the string breaks is given as 1.6 m/s (downwards), the distance to the floor is 0.52 m, and the acceleration due to gravity is 9.8 m/s².
We can use the equation:
\( s = ut + \frac{1}{2}at^2 \)
where s is the displacement (0.52 m), u is the initial velocity (1.6 m/s), a is the acceleration (9.8 m/s²), and t is the time we want to find.
\( 0.52 = 1.6t + \frac{1}{2} \times 9.8 \times t^2 \)
\( 0.52 = 1.6t + 4.9t^2 \)
This is a quadratic equation in the form of \( at^2 + bt + c = 0 \). We can solve for t using the quadratic formula:
\( t = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \)
Where \( a = 4.9 \), \( b = 1.6 \), and \( c = -0.52 \). Let’s calculate the values of t.
To solve the quadratic equation \( 4.9t^2 + 1.6t – 0.52 = 0 \), we will use the quadratic formula:
\( t = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \)
Here, \( a = 4.9 \), \( b = 1.6 \), and \( c = -0.52 \). Substituting these values into the formula gives:
\( t = \frac{-1.6 \pm \sqrt{1.6^2 – 4 \times 4.9 \times -0.52}}{2 \times 4.9} \)
\( t = \frac{-1.6 \pm \sqrt{2.56 + 10.192}}{9.8} \)
\( t = \frac{-1.6 \pm \sqrt{12.752}}{9.8} \)
\( \sqrt{12.752} \approx 3.57 \)
So, the equation becomes:
\( t = \frac{-1.6 \pm 3.57}{9.8} \)
This yields two solutions, but we will discard the negative time as it is not physically meaningful in this context. Thus:
\( t = \frac{-1.6 + 3.57}{9.8} \)
\( t \approx \frac{1.97}{9.8} \)
\( t \approx 0.201 \text{ seconds} \)
Therefore, the time taken for particle A to reach the floor after the string breaks is approximately 0.201 seconds.
Question
A cyclist exerts a constant driving force of magnitude F N while moving up a straight hill inclined at an angle α to the horizontal, where sin \(\alpha =\frac{36}{325}\) . A constant resistance to motion of 32 N acts on
the cyclist. The total weight of the cyclist and his bicycle is 780 N. The cyclist’s acceleration is −0.2 m s−2.
(i) Find the value of F.
The cyclist’s speed is 7 m s−1 at the bottom of the hill.
(ii) Find how far up the hill the cyclist travels before coming to rest.
▶️Answer/Explanation
(i)First, let’s establish the forces acting on the cyclist. The total weight of the cyclist and his bicycle is \( 780 \, \text{N} \). The component of this weight acting along the slope (parallel to the slope) can be found using the sine of the angle \( \alpha \).
Given \( \sin \alpha = \frac{36}{325} \), the parallel component of the weight is \( 780 \times \frac{36}{325} \).
The net force acting on the cyclist is the sum of the driving force \( F \), the resistance force (32 N acting opposite to the direction of motion), and the component of the weight acting along the slope (also acting opposite to the direction of motion).
According to Newton’s second law, \( F_{\text{net}} = ma \), where \( m \) is the mass, \( a \) is the acceleration, and \( F_{\text{net}} \) is the net force. We can rearrange this to \( F = ma + F_{\text{resistance}} + F_{\text{weight parallel}} \).
The mass \( m \) of the cyclist and bicycle can be found using \( m = \frac{Weight}{g} \), where \( g \) is the acceleration due to gravity (approximately \( 9.8 \, \text{m/s}^2 \)). So, \( m = \frac{780}{9.8} \).
Now, we can calculate \( F \):
\( F = m(-0.2) + 32 + 780 \times \frac{36}{325} \)
\( m = \frac{780}{9.8} \)
\( F = \frac{780}{9.8}(-0.2) + 32 + 780 \times \frac{36}{325} \)
\( F = 780 \times \left( -\frac{0.2}{9.8} + \frac{36}{325} \right) + 32 \)
\( F = 780 \times \left( -0.0204 + 0.1108 \right) + 32 \)
\( F = 780 \times 0.0904 + 32 \)
\( F = 70.512 + 32 \)
\( F \approx 102.512 \, \text{N} \)
So, the driving force \( F \) exerted by the cyclist is approximately \( 102.5 \, \text{N} \).
(ii) We need to find how far up the hill the cyclist travels before coming to rest. We know the initial speed at the bottom of the hill is \( 7 \, \text{m/s} \), and the final speed is \( 0 \, \text{m/s} \) (when the cyclist comes to rest). The acceleration is \( -0.2 \, \text{m/s}^2 \).
We can use the kinematic equation:
\( v^2 = u^2 + 2as \)
where \( v \) is the final velocity, \( u \) is the initial velocity, \( a \) is the acceleration, and \( s \) is the distance.
\( 0^2 = 7^2 + 2 \times (-0.2) \times s \)
\( 0 = 49 – 0.4s \)
\( 0.4s = 49 \)
\( s = \frac{49}{0.4} \)
\( s = 122.5 \, \text{m} \)
Therefore, the cyclist travels 122.5 meters up the hill before coming to rest.
Question
A car driver makes a journey in a straight line from A to B, starting from rest. The speed of the car increases to a maximum, then decreases until the car is at rest at B. The distance travelled by the car t seconds after leaving A is 0.000 011 7(400t3 − 3t4) metres.
(i) Find the distance AB.
(ii) Find the maximum speed of the car.
(iii) Find the acceleration of the car
(a) as it starts from A,
(b) as it arrives at B.
(iv) Sketch the velocity-time graph for the journey.
▶️Answer/Explanation
(i)The distance traveled by the car \( t \) seconds after leaving A is given by the equation \( s(t) = 0.0000117(400t^3 – 3t^4) \) meters. To find the total distance AB, we need to determine when the car comes to rest at B. This happens when the speed of the car is zero, which we can find by setting the derivative of \( s(t) \) equal to zero.
The velocity \( v(t) \) of the car at any time \( t \) is the first derivative of \( s(t) \):
\( v(t) = \frac{ds}{dt} = 0.0000117(1200t^2 – 12t^3) \)
Setting \( v(t) = 0 \) gives:
\( 0.0000117(1200t^2 – 12t^3) = 0 \)
\( 1200t^2 – 12t^3 = 0 \)
\( t^2(100 – t) = 0 \)
This gives us \( t = 0 \) (when the car starts) and \( t = 100 \) seconds (when the car stops at B). Thus, the total time taken for the journey is 100 seconds.
The distance AB can be found by substituting \( t = 100 \) seconds into the original distance equation:
\( AB = 0.0000117(400 \times 100^3 – 3 \times 100^4) \)
\( AB = 0.0000117(4000000 – 3000000) \)
\( AB = 0.0000117 \times 1000000 \)
\( AB = 11.7 \, \text{m} \)
So, the distance AB is 11.7 meters.
(ii)The maximum speed is found when the derivative of the velocity function (i.e., the acceleration) is zero. The acceleration \( a(t) \) is the derivative of the velocity function \( v(t) \):
\( a(t) = \frac{dv}{dt} = 0.0000117(2400t – 36t^2) \)
Setting \( a(t) = 0 \) gives:
\( 0.0000117(2400t – 36t^2) = 0 \)
\( 2400t – 36t^2 = 0 \)
\( t(66.67 – t) = 0 \]
This gives \( t = 0 \) (which we ignore since it’s the start of the journey) and \( t = 66.67 \) seconds. We substitute \( t = 66.67 \) into the velocity equation to find the maximum speed:
\( v_{\text{max}} = 0.0000117(1200 \times 66.67^2 – 12 \times 66.67^3) \)
Calculating \( v_{\text{max}} \):
\( v_{\text{max}} = 0.0000117(8000000 – 355555.56) \)
\( v_{\text{max}} \approx 0.0000117 \times 7644444.44 \)
\( v_{\text{max}} \approx 89.4 \, \text{m/s} \)
(iii)(a) As it starts from A
Since \( t = 0 \) at the start, we substitute \( t = 0 \) into the acceleration equation:
\( a(0) = 0.0000117(2400 \times 0 – 36 \times 0^2) \)
\( a(0) = 0 \, \text{m/s}^2 \)
(b) As it arrives at B:
Since \( t = 100 \) seconds at B, we substitute \( t = 100 \) into the acceleration equation:
\( a(100) = 0.0000117(2400 \times 100 – 36 \times 100^2) \)
\( a(100) = 0.0000117(240000 – 360000) \)
\( a(100) = 0.0000117 \times -120000 \)
\( a(100) = -1.404 \, \text{m/s}^2 \)
(iv): Sketching the Velocity-Time Graph
The velocity-time graph for this journey would start at \( v = 0 \) m/s (as the car starts from rest), increase to a maximum at \( t = 66.67 \) seconds, and then decrease back to \( v = 0 \) m/s at \( t = 100 \) seconds. It will be a parabolic curve that opens downwards, reflecting the increase and then decrease in velocity.
A parabolic curve peaking at around \( t = 66.67 \) seconds and \( v \approx 89.4 \) m/s.
Question
A train of mass 400 000 kg is moving on a straight horizontal track. The power of the engine is constant and equal to 1500 kW and the resistance to the train’s motion is 30 000 N. Find
(i) the acceleration of the train when its speed is 37.5 m s−1,
(ii) the steady speed at which the train can move.
▶️Answer/Explanation
(i)Driving Force (DF)
– Power of the engine, \( P = 1500 \, \text{kW} = 1500 \times 1000 \, \text{W} \)
– Speed, \( v = 37.5 \, \text{m/s} \)
– Driving Force (DF) is calculated as \( \mathrm{DF} = \frac{P}{v} = \frac{1500000}{37.5} = 40000 \, \text{N} \)
Net Force:
– Resistance, \( R = 30000 \, \text{N} \)
– Net Force, \( \mathrm{DF} – R = 40000 – 30000 = 10000 \, \text{N} \)
Acceleration:
– Using \( \mathrm{Net \, Force} = m \times a \)
– Mass of the train, \( m = 400000 \, \text{kg} \)
– Acceleration, \( a = \frac{\mathrm{Net \, Force}}{m} = \frac{10000}{400000} = 0.025 \, \text{m/s}^2 \)
(ii) At steady speed, the net force is zero, so the driving force equals the resistance force.
Steady Speed:
– Using \( P = Fv \), rearrange to find \( v \) when \( F = R \)
– Steady Speed, \( v_{\text{steady}} = \frac{P}{R} = \frac{1500000}{30000} = 50 \, \text{m/s} \)
Question
Particle P travels along a straight line from A to B with constant acceleration 0.05 m\( s^{−2}\) . Its speed at A is 2 m\( s^{−1}\) and its speed at B is 5 m \(s^{−1}\).
(i) Find the time taken for P to travel from A to B, and find also the distance AB.
Particle Q also travels along the same straight line from A to B, starting from rest at A. At time ts after leaving A, the speed of Q is kt3 m\( s^{−1}\) , where k is a constant. Q takes the same time to travel from A to B as P does.
(ii) Find the value of k and find Q’s speed at B.
▶️Answer/Explanation
(i) For Particle P:
We use the kinematic equation:
\( v_B = v_A + at \)
Given that \(v_A = 2 \, \text{m/s}\), \(v_B = 5 \, \text{m/s}\), and \(a = 0.05 \, \text{m/s}^2\), we can rearrange the equation to solve for \(t\):
\( 5 = 2 + 0.05t \)
Solving for \(t\), we get \(t = 60 \, \text{s}\).
Now, to find the distance AB, we can use the kinematic equation for displacement:
\( s = v_A t + \frac{1}{2} a t^2 \)
\( s = 2 \times 60 + \frac{1}{2} \times 0.05 \times 60^2 \)
\( s = 120 + \frac{1}{2} \times 0.05 \times 3600 \)
\( s = 120 + 90 \)
\( s = 210 \, \text{m} \)
So, the time taken for P to travel from A to B is 60 seconds, and the distance AB is 210 meters.
(ii) For Particle Q:
The velocity of Q at time \(t\) is given by \(kt^3\). Since Q takes the same time to travel from A to B as P does, the time \(t\) is the same (60 seconds).
Now, we find the displacement (\(s\)) by integrating the velocity function:
\( s = \int (kt^3) \, dt \)
Integrating, we get:
\( s = \frac{k}{4}t^4 + C \)
Since Q starts from rest at A, the constant of integration (\(C\)) is 0. Therefore, the displacement function is:
\( s = \frac{k}{4}t^4 \)
Now, we set up the equation \( 210 = \frac{k}{4} \times \frac{60^4}{4} \) to solve for \(k\):
\( 210 = \frac{k}{4} \times \frac{60^4}{4} \)
Solving for \(k\), we find \(k = \frac{7}{108000}\).
Finally, we find the speed of Q at B by evaluating \(kt^3\) at \(t = 60\) seconds:
\( \text{Speed at B} = \frac{7}{108000} \times 60^3 \)
\( \text{Speed at B} = 14 \, \text{m/s} \).
The speed of Q at B as \( 14 \, \text{m/s} \).
Question
The top of a cliff is 40 metres above the level of the sea. A man in a boat, close to the bottom of the cliff, is in difficulty and fires a distress signal vertically upwards from sea level. Find
(i) the speed of projection of the signal given that it reaches a height of 5 m above the top of the cliff,
(ii) the length of time for which the signal is above the level of the top of the cliff.
The man fires another distress signal vertically upwards from sea level. This signal is above the level of the top of the cliff for √(17) s.
(iii) Find the speed of projection of the second signal.
▶️Answer/Explanation
(i) Speed of Projection:
We use the kinematic equation for vertical motion:
\( v^2 = u^2 + 2as \)
where:
– \( v \) is the final velocity,
– \( u \) is the initial velocity,
– \( a \) is the acceleration (which is the acceleration due to gravity, \( g = 9.8 \, \text{m/s}^2 \)),
– \( s \) is the displacement.
The displacement (\( s \)) is \( -40 + 5 = -35 \) meters (negative because it is against gravity), and the initial velocity (\( u \)) is \( 0 \, \text{m/s} \) as it starts from rest.
\( v^2 = 0^2 + 2 \times (-9.8) \times (-35) \)
\( v = \sqrt{2 \times 9.8 \times 35} \approx 30 \, \text{m/s} \)
(ii)For the first signal, we use the kinematic equation for vertical motion:
\( s = ut + \frac{1}{2} a t^2 \)
Given \( s = 40 \, \text{m} \), \( u = 0 \, \text{m/s} \), and \( a = -9.8 \, \text{m/s}^2 \) (negative due to gravity), we get:
\( 40 = 0 \times t + \frac{1}{2} \times (-9.8) \times t^2 \)
Solving for \( t \), we find two solutions: \( t = 2 \) and \( t = 4 \).
Since we are interested in the time above the ground, the correct solution is \( t = 2 \) seconds.
For the second signal, the same equation applies:
\( s = ut + \frac{1}{2} a t^2 \)
Given \( s = 5 \, \text{m} \), \( u = 0 \, \text{m/s} \), and \( a = -9.8 \, \text{m/s}^2 \), we get:
\( 5 = 0 \times t + \frac{1}{2} \times (-9.8) \times t^2 \)
Solving for \( t \), we find \( t = 1 \) second.
Therefore, the time above the ground for both signals is \( 2 \) seconds.
(iii)The time of flight (\( T \)) for the second signal is given as \( \sqrt{17} \) seconds. Using the kinematic equation:
\( T = \frac{2u}{g} \)
Given \( T = \sqrt{17} \) and \( g = 9.8 \, \text{m/s}^2 \), we can solve for \( u \):
\( \sqrt{17} = \frac{2u}{9.8} \)
Solving for \( u \), we find \( u \approx 5 \, \text{m/s} \).
The maximum height above the top of the cliff is given by:
\( \text{Max. height} = \frac{1}{2} g T^2 \)
Substituting the values, we get:
\( \text{Max. height} = \frac{1}{2} \times 9.8 \times \left(\sqrt{17}\right)^2 \div 4 \approx 21.25 \)
Finally, the speed of projection for the second signal is given by:
\( V^2 = 2g \times \text{Max. height} \)
Solving for \( V \):
\( V = \sqrt{2 \times 9.8 \times 21.25} \approx 35 \, \text{m/s} \)
Question
Particle P travels along a straight line from A to B with constant acceleration 0.05 m\( s^{−2}\) . Its speed at A is 2 m\( s^{−1}\) and its speed at B is 5 m \(s^{−1}\).
(i) Find the time taken for P to travel from A to B, and find also the distance AB.
Particle Q also travels along the same straight line from A to B, starting from rest at A. At time ts after leaving A, the speed of Q is kt3 m\( s^{−1}\) , where k is a constant. Q takes the same time to travel from A to B as P does.
(ii) Find the value of k and find Q’s speed at B.
▶️Answer/Explanation
(i) For Particle P:
We use the kinematic equation:
\( v_B = v_A + at \)
Given that \(v_A = 2 \, \text{m/s}\), \(v_B = 5 \, \text{m/s}\), and \(a = 0.05 \, \text{m/s}^2\), we can rearrange the equation to solve for \(t\):
\( 5 = 2 + 0.05t \)
Solving for \(t\), we get \(t = 60 \, \text{s}\).
Now, to find the distance AB, we can use the kinematic equation for displacement:
\( s = v_A t + \frac{1}{2} a t^2 \)
\( s = 2 \times 60 + \frac{1}{2} \times 0.05 \times 60^2 \)
\( s = 120 + \frac{1}{2} \times 0.05 \times 3600 \)
\( s = 120 + 90 \)
\( s = 210 \, \text{m} \)
So, the time taken for P to travel from A to B is 60 seconds, and the distance AB is 210 meters.
(ii) For Particle Q:
The velocity of Q at time \(t\) is given by \(kt^3\). Since Q takes the same time to travel from A to B as P does, the time \(t\) is the same (60 seconds).
Now, we find the displacement (\(s\)) by integrating the velocity function:
\( s = \int (kt^3) \, dt \)
Integrating, we get:
\( s = \frac{k}{4}t^4 + C \)
Since Q starts from rest at A, the constant of integration (\(C\)) is 0. Therefore, the displacement function is:
\( s = \frac{k}{4}t^4 \)
Now, we set up the equation \( 210 = \frac{k}{4} \times \frac{60^4}{4} \) to solve for \(k\):
\( 210 = \frac{k}{4} \times \frac{60^4}{4} \)
Solving for \(k\), we find \(k = \frac{7}{108000}\).
Finally, we find the speed of Q at B by evaluating \(kt^3\) at \(t = 60\) seconds:
\( \text{Speed at B} = \frac{7}{108000} \times 60^3 \)
\( \text{Speed at B} = 14 \, \text{m/s} \).
The speed of Q at B as \( 14 \, \text{m/s} \).
Question
A particle P starts at the point O and travels in a straight line. At time t seconds after leaving O the
velocity of P is vm\( s^{−1}\), where v = 0.75t2 − \(0.0625t ^{3}\) . Find
(i) the positive value of t for which the acceleration is zero,
(ii) the distance travelled by P before it changes its direction of motion
▶️Answer/Explanation
(i) The given acceleration function is \( a = 1.5t – 0.1875t^2 \). To find when the acceleration is zero, we set \( a = 0 \):
\( 0.1875t(8 – t) = 0 \)
This equation is equivalent to \( t(8 – t) = 0 \). The solutions to this equation are \( t = 0 \) and \( t = 8 \). However, since the particle starts at \( O \) at \( t = 0 \), the relevant solution is \( t = 8 \), which is the time at which the acceleration is zero.
(ii) The velocity function is \( v = 0.75t^2 – 0.0625t^3 \). To find when the particle changes its direction, we set \( v = 0 \):
\( 0.75t^2 – 0.0625t^3 = 0 \)
Factoring out \( t^2 \) from the terms, we get \( t^2(0.75 – 0.0625t) = 0 \). The solutions to this equation are \( t = 0 \) (which is the initial time) and \( t = \frac{0.75}{0.0625} = 12 \). The relevant solution is \( t = 12 \), indicating the time at which the particle changes its direction.
(iii) The displacement (\( s \)) is given by the integral of the velocity function:\
\( s = \int v \, dt \)
Integrating \( v = 0.75t^2 – 0.0625t^3 \),
\( s = \frac{0.75}{3}t^3 – \frac{0.0625}{4}t^4 + C \)
Now, we find the total distance traveled by evaluating this expression from \( t = 0 \) to \( t = 12 \):
\( s = \left[\frac{0.75}{3} \times 12^3 – \frac{0.0625}{4} \times 12^4\right] \)
After evaluating this expression, you correctly obtained \( s = 108 \, \text{m} \), which is the distance traveled by the particle before changing its direction.