Question
A particle of mass 0.4 kg is released from rest at a height of 1.8 m above the surface of the water in a
tank. There is no instantaneous change of speed when the particle enters the water. The water exerts an upward force of 5.6 N on the particle when it is in the water.
(i) Find the velocity of the particle at the instant when it reaches the surface of the water.
(ii) Find the time that it takes from the instant when the particle enters the water until it comes to instantaneous rest in the water. You may assume that the tank is deep enough so that the particle does not reach the bottom of the tank.
(iii) Sketch a velocity-time graph for the motion of the particle from the instant at which it is released
until it comes to instantaneous rest in the water.
▶️Answer/Explanation
(i) Velocity just before entering the water:
The potential energy lost by the particle is converted into kinetic energy just before entering the water. The potential energy lost is given by \( mgh \), where \( m \) is the mass, \( g \) is the acceleration due to gravity, and \( h \) is the height.
\( \text{Potential energy lost} = mgh \)
This potential energy is converted into kinetic energy just before entering the water:
\( \frac{1}{2}m\nu^2 = mgh \)
Solving for \( \nu \):
\( \nu = \sqrt{2gh} \)
Substitute \( g = 9.8 \, \text{m/s}^2 \) and \( h = 1.8 \, \text{m} \):
\( \nu = \sqrt{2 \times 9.8 \, \text{m/s}^2 \times 1.8 \, \text{m}} \)
\( \nu = 6 \, \text{m/s} \)
(ii) Time taken to come to rest in the water:
Once in the water, the net force acting on the particle is the difference between the buoyant force (\(5.6 \, \text{N}\)) and its weight (\(mg\)). The net force is then used to find the deceleration.
\( F_{\text{net}} = 5.6 \, \text{N} – 0.4 \, \text{kg} \times 9.8 \, \text{m/s}^2 \)
Calculate \( F_{\text{net}} \):
\( F_{\text{net}} = -3.6 \, \text{N} \)
\( a = \frac{F_{\text{net}}}{m} = -4 \, \text{m/s}^2 \)
Now, we’ll use the kinematic equation \( \nu = u + at \), where \( u \) is the initial velocity (velocity just before entering water), \( a \) is the deceleration, and \( t \) is the time.
\( \nu = 0 \) (since the particle comes to rest)
Solve for \( t \):
\( 0 = \sqrt{2gh} + at \)
\( t = 1.5 \, \text{s} \)
(iii) Velocity-time graph:
The graph starts at the origin (0,0) with a positive gradient, indicating a linear increase in velocity during free fall. After entering the water, there’s a second straight line with a negative gradient, indicating a linear decrease in velocity until the particle comes to rest. The graph finishes at (2.1, 0), showing that the velocity becomes zero at \( t = 2.1 \) seconds.
Question
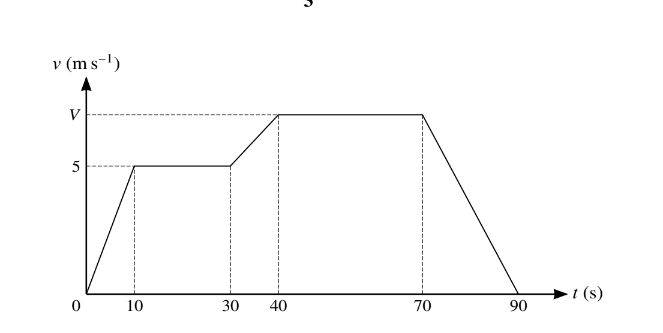
An elevator moves vertically, supported by a cable. The diagram shows a velocity-time graph which models the motion of the elevator. The graph consists of 7 straight line segments.
The elevator accelerates upwards from rest to a speed of \(2ms^{-1}\) over a period of 1.5s and then travels at this speed for before decelerating to rest over a period of 1 s.
The elevator then remains at rest for 6 s. before accelerating to a speed of \( Vms^{-1}\) downwards over a period of 2s. The elevator travels at this speed for a period of 5s, before decelerating to rest over a period of 1.5s.
(a) Find the acceleration of the elevator during the first 1.5s.
(b) Given that the elevator starts and finishes its journey on the ground floor, find V.
(c) The combined weight of the elevator and passengers on its upward journey is 1500kg. Assuming that there is no resistance to motion, find the tension in the elevator cable on its upward journey when the elevator is decelerating.
▶️Answer/Explanation
(a) Acceleration during the first \(1.5 \, \text{s}\):
The formula for acceleration is \(a = \frac{\Delta v}{\Delta t}\), where \(\Delta v\) is the change in velocity and \(\Delta t\) is the change in time.
In the given velocity-time graph, during the first \(1.5 \, \text{s}\), the elevator accelerates from rest to a speed of \(2 \, \text{m/s}\). Therefore, the change in velocity \(\Delta v\) is \(2 \, \text{m/s}\), and the change in time \(\Delta t\) is \(1.5 \, \text{s}\). Plug these values into the formula to find the acceleration \(a\):
\( a = \frac{2 \, \text{m/s}}{1.5 \, \text{s}} = \frac{4}{3} \, \text{m/s}^2 \)
(b) Find \(V\):
For this part, we consider the downward journey. The equation of motion for constant acceleration is given by:
\( s = ut + \frac{1}{2} a t^2 \)
For the first segment (acceleration), \(s_1 = \frac{1}{2} a t_1^2\) where \(a = \frac{4}{3} \, \text{m/s}^2\) and \(t_1 = 1.5 \, \text{s}\).
For the second segment (constant velocity), \(s_2 = V t_2\) where \(V\) is the constant velocity and \(t_2 = 1 \, \text{s}\).
For the third segment (deceleration), \(s_3 = \frac{1}{2} a t_3^2\) where \(a = -2 \, \text{m/s}^2\) and \(t_3 = 1.5 \, \text{s}\)
The total displacement is given by \(s_1 + s_2 + s_3\) and is set equal to zero since the elevator starts and finishes at the same position. Substituting the known values into the equation and solving for \(V\) gives:
\( \frac{1}{2} \left(\frac{4}{3}\right) \times (1.5)^2 + V \times 1 + \frac{1}{2} \times (-2) \times (1.5)^2 = 0 \)
Solving this equation yields \(V = 1.70 \, \text{m/s}\) (rounded to three significant figures).
(c) Tension during upward journey when decelerating:
Use Newton’s second law \(\Sigma F = ma\). The net force is \(T – mg\), where \(T\) is the tension, \(m\) is the mass of the elevator and passengers (\(1500 \, \text{kg}\)), \(g\) is the acceleration due to gravity (\(9.8 \, \text{m/s}^2\)), and \(a\) is the acceleration during deceleration (\(-2 \, \text{m/s}^2\)).
\( T – mg = ma \)
\( T – 1500 \times 9.8 = 1500 \times (-2) \)
Solving this equation gives \(T = 12000 \, \text{N}\).
Question
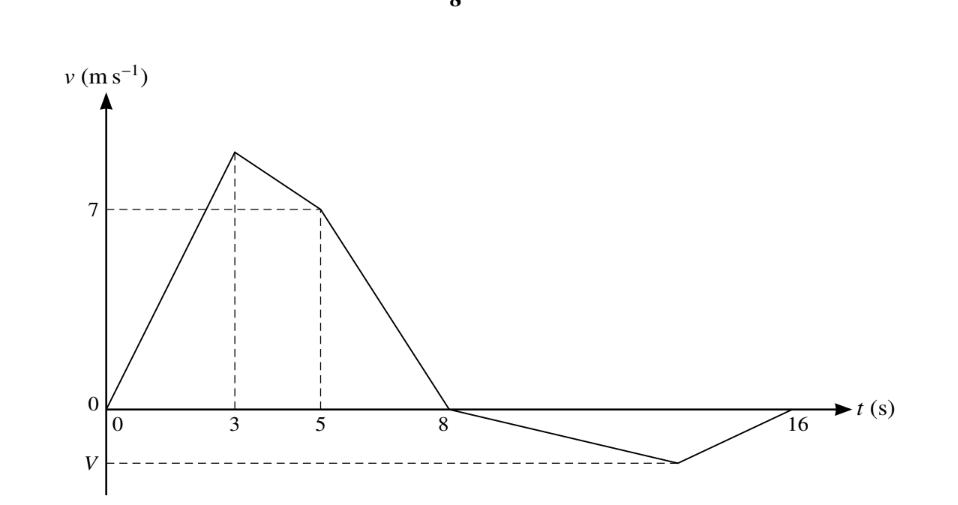
The velocity of a particle moving in a straight line is v \(ms^{-1}\)at time t seconds after leaving a fixed
point O. The diagram shows a velocity-time graph which models the motion of the particle from t = 0to t = 16. The graph consists of five straight line segments. The acceleration of the particle from t = 0 to t = 3 is 3 \(ms^{-2}\)
The velocity of the particle at t = 5 is 7 m s^{-1} and it comes to instantaneous rest at t = 8. The particle then comes to rest again at t = 16. The minimum velocity of the particle is V m s^{-1}.
(i) Find the distance travelled by the particle in the first 8 s of its motion.
(ii) Given that when the particle comes to rest at t = 16 its displacement from O is 32 m, find the value of V.
▶️Answer/Explanation
(i) Distance traveled by the particle in the first 8 seconds:
The velocity-time graph consists of five straight line segments. The first segment is from \(t=0\) to \(t=3\), during which the acceleration is \(3 \, \text{m/s}^2\). This means the velocity is increasing linearly during this interval.
The area under the velocity-time graph represents the distance traveled. For the first segment, this area is the area of a trapezium:
\( \text{Area}_{\text{segment 1}} = \frac{1}{2} \times \text{base}_1 \times (\text{height}_1 + \text{height}_2) \)
\( \text{Area}_{\text{segment 1}} = \frac{1}{2} \times 3 \times (0 + 9) \)
Next, there’s a constant velocity segment from \(t=3\) to \(t=5\) with a velocity of \(9 \, \text{m/s}\). The area of this segment is a rectangle:
\( \text{Area}_{\text{segment 2}} = \text{base}_2 \times \text{height}_2 \)
\( \text{Area}_{\text{segment 2}} = 2 \times 9 \)
Finally, there’s another accelerating segment from \(t=5\) to \(t=8\) with a constant acceleration of \(3 \, \text{m/s}^2\). The area of this trapezium is:
\( \text{Area}_{\text{segment 3}} = \frac{1}{2} \times \text{base}_3 \times (\text{height}_2 + \text{height}_3) \)
\( \text{Area}_{\text{segment 3}} = \frac{1}{2} \times 3 \times (9 + 7) \)
Now, add up these three areas to find the total distance traveled in the first 8 seconds:
\( \text{Total Distance} = \text{Area}_{\text{segment 1}} + \text{Area}_{\text{segment 2}} + \text{Area}_{\text{segment 3}} \)
\( \text{Total Distance} = \frac{1}{2} \times 3 \times 9 + 2 \times 9 + \frac{1}{2} \times 3 \times (9 + 7) \)
\( \text{Total Distance} = 40 \, \text{m} \)
(ii) Finding the value of \(\mathrm{V}\) when the particle comes to rest at \(t=16\):
The displacement during the time interval from \(t=8\) to \(t=16\) is given by the area under the graph during that time. This area is \(-8 \, \text{m}\), and it represents the area of a triangle with base \(8\) and height \(\mathrm{V}\). So,
\( \text{Area}_{\text{triangle}} = \frac{1}{2} \times 8 \times \mathrm{V} \)
\( -8 = 4 \times \mathrm{V} \)
Solving for \(\mathrm{V}\):
\( \mathrm{V} = -2 \, \text{m/s} \)
This means the minimum velocity of the particle is \(-2 \, \text{m/s}\) at the point it comes to rest at \(t=16\).
Question
A particle P moves in a straight line starting from a point O and comes to rest 35 s later. At time ts after leaving O, the velocity v \(ms^{-1}\) of P is given by
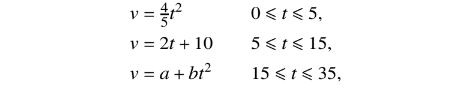
where a and b are constants such that a > 0 and b < 0.
(i) Show that the values of a and b are 49 and −0.04 respectively.
(ii) Sketch the velocity-time graph.
(iii) Find the total distance travelled by P during the 35 s.
Answer/Explanation
Question
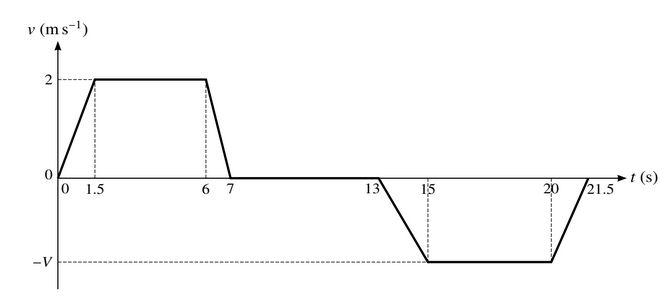
The diagram shows a velocity-time graph which models the motion of a cyclist. The graph consists
of five straight line segments. The cyclist accelerates from rest to a speed of 5\( ms^{-1}\) over a period of 10 s, and then travels at this speed for a further 20 s. The cyclist then descends a hill, accelerating to speed V\( m s^{-1}\)over a period of 10 s. This speed is maintained for a further 30 s. The cyclist thendecelerates to rest over a period of 20 s.
(i) Find the acceleration of the cyclist during the first 10 seconds.
(ii) Show that the total distance travelled by the cyclist in the 90 seconds of motion may be expressed
as(45V + 150) m. Hence find V, given that the total distance travelled by the cyclist is 465 m. (iii) The combined mass of the cyclist and the bicycle is 80 kg. The cyclist experiences a constant resistance to motion of 20 N. Use an energy method to find the vertical distance which the cyclist descends during the downhill section from t = 30 to t = 40, assuming that the cyclist does no work during this time.
▶️Answer/Explanation
(i) Acceleration during the first 10 seconds:
The cyclist accelerates from rest to a speed of \(5 \, \text{m/s}\) over a period of \(10 \, \text{s}\). Acceleration (\(a\)) is given by the formula \(a = \frac{\Delta v}{\Delta t}\), where \(\Delta v\) is the change in velocity and \(\Delta t\) is the time interval.
In this case, the change in velocity (\(\Delta v\)) is \(5 \, \text{m/s}\) (initial velocity is \(0 \, \text{m/s}\) as the cyclist starts from rest), and the time interval (\(\Delta t\)) is \(10 \, \text{s}\).
So, \(a = \frac{5 \, \text{m/s}}{10 \, \text{s}} = 0.5 \, \text{m/s}^2\).
(ii) Total distance travelled by the cyclist:
The total distance (\(S\)) can be found by adding the areas under each segment of the velocity-time graph.
– First segment (10 seconds): Area = \(\frac{1}{2} \times 10 \times 5 = 25 \, \text{m}\)
– Second segment (20 seconds):Area = \(10 \times 5 = 50 \, \text{m}\)
– Third segment (10 seconds):Area = \(\frac{1}{2} \times 10 \times (5 + V)\)
– Fourth segment (30 seconds):Area = \(10 \times V\)
– Fifth segment (20 seconds):Area = \(\frac{1}{2} \times 20 \times V = 10V\)
The total distance is \(S = 25 + 50 + \frac{1}{2} \times 10 \times (5 + V) + 10V = 150 + 45V\).
Given that \(S = 465 \, \text{m}\), we can set up the equation \(150 + 45V = 465\) to solve for \(V\).
\(
\begin{aligned}
150 + 45V &= 465 \\
45V &= 315 \\
V &= 7 \, \text{m/s}
\end{aligned}
\)
(iii) Vertical distance descended during the downhill section:**
The energy method involves equating the potential energy lost to the work done against resistance. The potential energy lost is \(mgh\), where \(m\) is the mass, \(g\) is the acceleration due to gravity, and \(h\) is the vertical distance.
The work done against resistance is the force multiplied by the distance, \(20 \, \text{N} \times h\).
Setting these equal, we get:
\(mgh = 20 \times h\)
Substitute \(m = 80 \, \text{kg}\), \(g = 9.8 \, \text{m/s}^2\), and solve for \(h\):
\(
\begin{aligned}
& 80 \times 9.8 \times h = 20 \times h \\
& 784h = 20h \\
& h = \frac{20}{784} \\
& h \approx 0.0255 \, \text{m} \, (\text{or} \, 2.55 \, \text{cm})
\end{aligned}
\)
This represents the vertical distance descended during the downhill section.