Two small smooth spheres A and B, of equal radii and of masses km kg and m kg respectively, where k > 1, are free to move on a smooth horizontal plane. A is moving towards B with speed 6 m s−1 and B is moving towards A with speed 2 m s−1. After the collision A and B coalesce and move with speed 4 m s−1.
(a) Question
Find k.
▶️Answer/Explanation
(a) Finding \(k\):
Using the conservation of linear momentum:
\( km \times 6 – m \times 2 = (km + m) \times 4 \)
\( k = 3 \)
(b) Question
Find, in terms of m, the loss of kinetic energy due to the collision.
▶️Answer/Explanation
(b) Finding the Loss of Kinetic Energy:
The initial kinetic energy (\(KE_{\text{initial}}\)) is the sum of the kinetic energies of A and B:
\( KE_{\text{initial}} = \frac{1}{2} \times k m \times 6^2 + \frac{1}{2} \times m \times (-2)^2 \)
The final kinetic energy (\(KE_{\text{final}}\)) is the kinetic energy of the coalesced mass:
\( KE_{\text{final}} = \frac{1}{2} \times (k m + m) \times 4^2 \)
The loss of kinetic energy (\(\Delta KE\)) is given by:
\(\Delta KE = KE_{\text{initial}} – KE_{\text{final}} \)
Substitute the values for \(k\) and \(m\):
\( \Delta KE = 24 \, \text{m} \, \text{J} \)
Question
A particle B of mass 5 kg is at rest on a smooth horizontal table. A particle A of mass 2.5 kg moves on the table with a speed of 6 m s−1 and collides directly with B. In the collision the two particles coalesce.
(a) Find the speed of the combined particle after the collision.
(b) Find the loss of kinetic energy of the system due to the collision.
▶️Answer/Explanation
(a) Finding the Speed of the Combined Particle after the Collision:
Using the conservation of linear momentum:
\( m_A \cdot v_A + m_B \cdot v_B = (m_A + m_B) \cdot v_f \)
Substituting the given values:
\( 6 \times 2.5 + 5 \times 0 = (2.5 + 5) \times v_f \)
Solving for \(v_f\):
\( v_f = \frac{15}{7} \, \text{m/s} \)
(b) Finding the Loss of Kinetic Energy:
Using the kinetic energy formula \(KE = \frac{1}{2} m v^2\) either before or after the collision:
Before the collision:
\( KE_{\text{initial}} = 0.5 \times 2.5 \times 6^2 \)
After the collision:
\( KE_{\text{final}} = 0.5 \times (2.5 + 5) \times \left(\frac{15}{7}\right)^2 \)
The loss of kinetic energy (\(\Delta KE\)) is given by:
\( \Delta KE = KE_{\text{initial}} – KE_{\text{final}} \)
Now, substitute the values and calculate \(\Delta KE\):
\( \Delta KE = 30 \, \text{J} \)
Question
Two particles P and Q of masses kg and kg respectively are free to move in a horizontal straight line on a smooth horizontal plane. P is projected towards Q with speed \(0.5ms^{-1}\). At the same instant Q is projected towards P with speed \(1ms^{-1}\). Q comes to rest in the resulting collision.
Find the speed of P after the collision.
▶️Answer/Explanation
The conservation of linear momentum equation is:
\( m_Pv_P + m_Qv_Q = (m_P + m_Q)v_f \)
Substitute the given values:
\( 0.2 \times 0.5 + 0.3 \times (-1) = (0.3-0.2) \times v_f \)
Now, let’s solve for \(v_f\):
\( -0.1 = 0.1 \times v_f \)
Solving for \(v_f\), we get:
\( v_f = -1 \, \text{m/s} \)
So, the correct speed of \(P\) after the collision is \(1 \, \text{m/s}\).
Question
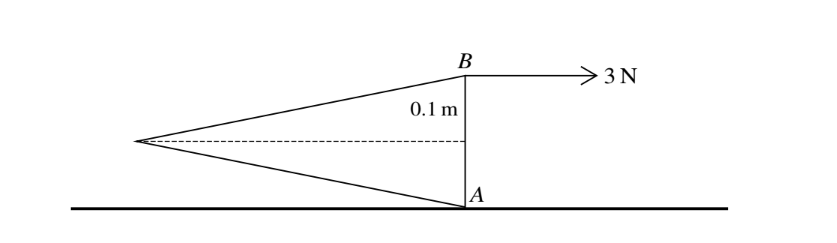
A uniform solid cone has weight 5 N and base radius 0.1 m. AB is a diameter of the base of the cone.
The cone is held in equilibrium, with A in contact with a rough horizontal surface and AB vertical, by a force applied at B. This force has magnitude 3 N and acts parallel to the axis of the cone (see
diagram). Calculate the height of the cone.
▶️Answer/Explanation
Vertical forces:
In the vertical direction, the weight of the cone (\( W \)) and the normal force (\( N \)) must balance each other.
\( N = W \)
\( N = 5 \, \text{N} \)
Torque (Moment) about point A:
The force applied at B creates a torque about point A. The torque (\( \tau \)) is given by the product of the force (\( F \)) and the perpendicular distance (\( r \)) from the line of action of the force to point A. The perpendicular distance is the radius of the base (\( r \)).
\( \tau = F \cdot r \)
\( \tau = 3 \, \text{N} \cdot 0.1 \, \text{m} = 0.3 \, \text{Nm} \)
Torque due to the weight of the cone:
The weight of the cone creates a torque about point A. The weight acts vertically downward at the center of mass, which is located at \( \frac{1}{3} \) of the height of the cone (\( h \)). The perpendicular distance (\( d’ \)) from the line of action of the weight to point A is \( \frac{2}{3} \) of the height.
\( \tau’ = W \cdot d’ \)
\( \tau’ = 5 \, \text{N} \cdot \frac{2}{3}h \)
Since the cone is in equilibrium, the torques about point A must balance:
\( \tau = \tau’ \)
\( 0.3 \, \text{Nm} = 5 \, \text{N} \cdot \frac{2}{3}h \)
\( h = \frac{0.3}{5} \times \frac{3}{2} \, \text{m} \)
\( h = 0.03 \, \text{m} \)
So, the height of the cone is \(0.03 \, \text{m}\) or \(3 \, \text{cm}\).