A bead, A, of mass 0.1 kg is threaded on a long straight rigid wire which is inclined at sin−1 \(\left ( \frac{7}{25} \right )\) to the horizontal. A is released from rest and moves down the wire. The coefficient of friction between A and the wire is μ. When A has travelled 0.45m down the wire, its speed is 0.6 m s−1.
Another bead, B, of mass 0.5 kg is also threaded on the wire. At the point where A has travelled 0.45 m down the wire, it hits B which is instantaneously at rest on the wire. A is brought to instantaneous rest in the collision. The coefficient of friction between B and the wire is 0.275.
(a) Question
Show that – = 0.25.
▶️Answer/Explanation
(a) Using Work-Energy Principle:
The work done by the friction force is equal to the change in kinetic energy:
\( W_{\text{friction}} = \mu mgh \)
The change in kinetic energy is given by:
\( \Delta KE = \frac{1}{2}mv^2 \)
Equating the work done by friction to the change in kinetic energy:
\( \mu mgh = \frac{1}{2}mv^2 \)
Given data:
\( m = 0.1 \, \text{kg}, \quad \sin^{-1}\left(\frac{7}{25}\right) \approx 16.3^\circ, \quad h = 0.45 \, \text{m}, \quad v = 0.6 \, \text{m/s} \)
Acceleration (\(a\)):
\( 0.6^2 = 0 + 2a \times 0.45 \)
Solving for \(a\):
\( a = 0.4 \, \text{m/s}^2 \)
Normal Reaction (\(R\)):
\( R = 0.1g \cos \alpha = 0.1g \times \cos 16.3^\circ \approx 0.96 \, \text{N} \)
Equating Forces along the Inclined Plane:
\( 0.1g \times \frac{7}{25} – F = 0.1g \times 0.4 \)
Solving for \(F\):
\( F = 0.24 \, \text{N} \)
Expressing Friction Force (\(F\)) in terms of \(\mu\):
\( F = \mu \times 0.1g \times \frac{24}{25} \)
Solving for \(\mu\):
\( \mu = \frac{0.24 \times 25}{24} = 0.25 \)
Therefore, \(\mu = 0.25\).
(b) Question
Find the time from when the collision occurs until A collides with B again.
▶️Answer/Explanation
(b)Using Conservation of Energy for Bead A:
\( 0.1 \times 0.6 = 0.5 \times v \)
\( v = 0.12 \, \text{m/s} \)
Equating Forces for Bead B:
\( 0.5g \times \frac{7}{25} – 0.275 \times 0.5g \times \frac{24}{25} = 0.5a \)
\( a = 0.16 \, \text{m/s}^2 \)
Equations of Motion for Beads A and B:
– For Bead A:
\( s_A = \frac{1}{2} \times 0.4t^2 \)
– For Bead B:
\( s_B = 0.12t + \frac{1}{2} \times 0.16t^2 \)
Equating Positions of Beads A and B:
\( \frac{1}{2} \times 0.4t^2 = 0.12t + \frac{1}{2} \times 0.16t^2 \)
Solving for \(t\):
Combine like terms and solve for \(t\):
\( 0.1t^2 – 0.12t – 0.12 = 0 \)
Solve this quadratic equation to find \(t\).
\(t = 1 \, \text{s}\), which is the required time.
A particle of mass 12 kg is stationary on a rough plane inclined at an angle of 250 to the horizontal. A force of magnitude P N acting parallel to a line of greatest slope of the plane is used to prevent the particle sliding down the plane. The coefficient of friction between the particle and the plane is 0.35.
(a) Question
Draw a sketch showing the forces acting on the particle.
▶️Answer/Explanation
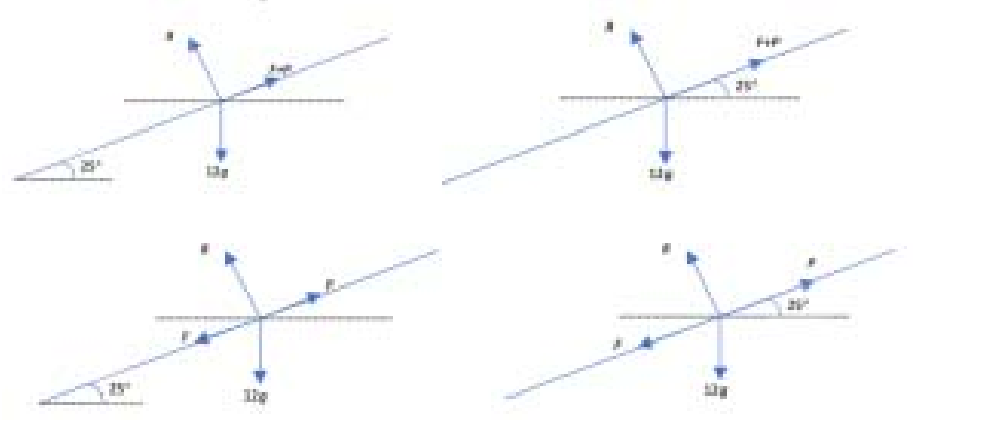
(b) Question
Find the least possible value of P.
▶️Answer/Explanation
P + F = 12g sin 25 =50.7
R =12g cos 25 = 108.8
F = 120 cos 25 × 0.35 = 38.1
P + 38.1 = 120 sin 25
P = 12.6
Question
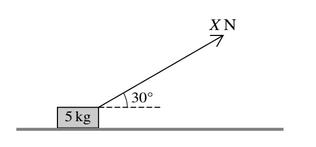
A block of mass 5kg is being pulled along a rough horizontal floor by a force of magnitude X N acting at \(30^o\) above the horizontal (see diagram). The block starts from rest and travels 2m in the first 5s of its motion.
(a) Find the acceleration of the block
(b) Given that the coefficient of friction between the block and the floor is 0.4, find X.
The block is now placed on a part of the floor where the coefficient of friction between the block and the floor has a different value. The value of X is changed to 25, and the block is now in limiting equilibrium.
(c) Find the value of the coefficient of friction between the block and this part of the floor.
▶️Answer/Explanation
(a) Finding the Acceleration (\(a\)):
Use the kinematic equation for uniformly accelerated motion:
\( s = ut + \frac{1}{2}at^2 \)
Given that the block starts from rest (\(u = 0\)), travels \(2 \, \text{m}\), and \(t = 5 \, \text{s}\):
\(2 = \frac{1}{2}a(5^2) \)
Solve for \(a\):
\(a = \frac{2}{\frac{1}{2} \times 5^2} = \frac{2}{\frac{1}{2} \times 25} = \frac{2}{\frac{25}{2}} = \frac{4}{25} \, \text{m/s}^2 \)
\( a = 0.16 \, \text{m/s}^2 \)
(b) Finding \(X\) with Coefficient of Friction \(0.4\):
In the horizontal direction:
\( X \cos(30^\circ) – f = ma \)
The frictional force (\(f\)) is given by \(f = \mu mg\), where \(\mu = 0.4\).
\( X \cos(30^\circ) – 0.4mg = m \cdot \frac{4}{25} \)
Assuming \(g = 9.8 \, \text{m/s}^2\):
\( X \cos(30^\circ) – 0.4 \times 5 \times 9.8 = 5 \cdot \frac{4}{25} \)
Solve for \(X\):
\( X = 19.5 \, \text{N} \)
(c) Finding Coefficient of Friction with \(X = 25\):
In limiting equilibrium, the frictional force is at its maximum, so \(f_{\text{max}} = \mu_{\text{max}} mg\).
In the horizontal direction:
\( X \cos(30^\circ) – f_{\text{max}} = 0 \)
Substituting \(X = 25\) and solve for \(\mu_{\text{max}}\):
\( R = 5g – 25 \sin(30^\circ) = 37.5 \, \text{N} \)
\( F = 25 \cos(30^\circ) = \frac{25 \sqrt{3}}{2} \, \text{N} \)
\( \mu = \frac{F}{R} = \frac{\frac{25 \sqrt{3}}{2}}{37.5} = 0.577 \)
Question
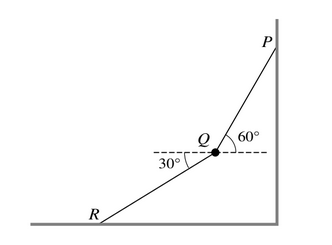
A particle Q of mass 0.2 kg is held in equilibrium by two light inextensible strings PQ and QR. P is a fixed point on a vertical wall and R is a fixed point on a horizontal floor. The angles which strings PQ and QR make with the horizontal are \(60^o\) and \(30^o\) respectively (see diagram)
Find the tensions in the two strings.
▶️Answer/Explanation
Resolving Forces and Setting Up Equations:
Vertical Component Equilibrium:
\( T_P \cos(60^\circ) = T_R \cos(30^\circ) \)
Vertical Component Equilibrium:
\( T_P \sin(60^\circ) = T_R \sin(30^\circ) + 0.2g \)
Solve these two equations simultaneously to find \(T_P\) and \(T_R\):
\( T_P = 3.46 \, \text{N} \)
\( T_R = 2 \, \text{N} \)
Alternative Method:
Using the sine rule:
\( \frac{T_P}{\sin(60^\circ)} = \frac{T_R}{\sin(150^\circ)} = \frac{0.2g}{\sin(150^\circ)} \]
Solving for \(T_P\) or \(T_R\):
\( T_P = 3.46 \, \text{N} \)
\( T_R = 2 \, \text{N} \)
Question
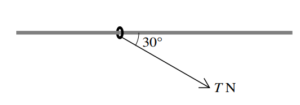
The diagram shows a ring of mass 0.1 kg threaded on a fixed horizontal rod. The rod is rough and the
coefficient of friction between the ring and the rod is 0.8. A force of magnitude T N acts on the ring
in a direction at 30Å to the rod, downwards in the vertical plane containing the rod. Initially the ring
is at rest.
(a) Find the greatest value of T for which the ring remains at rest.
(b) Find the acceleration of the ring when T = 3.
▶️Answer/Explanation
(a) Finding the Greatest Value of \(T\) for Rest:
Resolve forces in the vertical and horizontal directions:
\( R = T \sin(30^\circ) + 0.1g \)
\( F = T \cos(30^\circ) \)
Set up the equation for equilibrium:
\( T \cos(30^\circ) = 0.8(T \sin(30^\circ) + 0.1g) \)
Solve for \(T\):
\( T = 1.72 \)
(b) Finding the Acceleration when \(T = 3\):
Resolve forces in the vertical and horizontal directions:
\( R = 3 \sin(30^\circ) + 0.1g \)
Set up the equation for the horizontal direction using Newton’s second law:
\( 3 \cos(30^\circ) – 0.8(3 \sin(30^\circ) + 0.1g) = 0.1a \)
Solve for \(a\):
\( a = 5.98 \, \text{m/s}^2 \)
Question
Two particles A and B, of masses m kg and 0.3 kg respectively, are attached to the ends of a light
inextensible string. The string passes over a fixed smooth pulley and the particles hang freely below
it. The system is released from rest, with both particles 0.8 m above horizontal ground. Particle A reaches the ground with a speed of\( 0.6 ms^{-1}\)
(i) Find the tension in the string during the motion before A reaches the ground.
(ii) Find the value of m.
▶️Answer/Explanation
(i) Tension in the String:
Using the kinematic equation for Particle A:
\( 0.6^2 = 0 + 2a \times 0.8 \)
\( a = 0.225 \, \text{m/s}^2 \)
For Particle A (\(m\)):
\( T – 0.3g = 0.3a \)
\( T = 0.3g + 0.3a \)
\( T = 3.07 \, \text{N} \)
(ii) Value of \(m\):
Using Newton’s second law for Particle B:
\( mg – T = ma \)
\( m(10 – 0.225) = 3.07 \)
\( m = \frac{3.07}{9.775} \)
\( m = 0.314 \, \text{kg} \)
Question
A car of mass 1800 kg is towing a trailer of mass 400 kg along a straight horizontal road. The car and
trailer are connected by a light rigid tow-bar. The car is accelerating at 1.5 m s−2. There are constant
resistance forces of 250 N on the car and 100 N on the trailer.
(a) Find the tension in the tow-bar.
(b) Find the power of the engine of the car at the instant when the speed is 20 m s−1.
▶️Answer/Explanation
(a)The tension in the tow-bar is the force transmitted through the tow-bar from the car to the trailer. We can use Newton’s second law to find this tension.
For the car:
\( F_{\text{car}} = m_{\text{car}} \cdot a_{\text{car}} + R_{\text{car}} \)
For the trailer:
\( F_{\text{trailer}} = m_{\text{trailer}} \cdot a_{\text{trailer}} + R_{\text{trailer}} \)
The tension in the tow-bar (\(T\)) is the force transmitted from the car to the trailer:
\( T = m_{\text{trailer}} \cdot a_{\text{trailer}} + R_{\text{trailer}} \)
Given data:
\( m_{\text{car}} = 1800 \, \text{kg}, \quad a_{\text{car}} = 1.5 \, \text{m/s}^2, \quad R_{\text{car}} = 250 \, \text{N} \)
\( m_{\text{trailer}} = 400 \, \text{kg}, \quad a_{\text{trailer}} = a_{\text{car}}, \quad R_{\text{trailer}} = 100 \, \text{N} \)
Substituting these values into the equation for \(T\):
\( T = (400 \cdot 1.5) + 100 \)
\( T = 600 + 100 \)
\( T = 700 \, \text{N} \)
So, the tension in the tow-bar is \(700 \, \text{N}\).
(b)Given forces:
\( F_{\text{total}} = F_{\text{car}} + F_{\text{trailer}} + R_{\text{car}} + R_{\text{trailer}} \)
Given:
\( m_{\text{car}} = 1800 \, \text{kg}, \quad a_{\text{car}} = 1.5 \, \text{m/s}^2, \quad R_{\text{car}} = 250 \, \text{N} \)
\( m_{\text{trailer}} = 400 \, \text{kg}, \quad a_{\text{trailer}} = a_{\text{car}}, \quad R_{\text{trailer}} = 100 \, \text{N} \)
Using Newton’s second law for the system:
\( F_{\text{total}} = (m_{\text{car}} + m_{\text{trailer}}) \cdot a_{\text{car}} + R_{\text{car}} + R_{\text{trailer}} \)
Substituting the given values:
\( F_{\text{total}} = (1800 + 400) \cdot 1.5 + 250 + 100 \)
\( F_{\text{total}} = 2200 \cdot 1.5 + 250 + 100 \)
\( F_{\text{total}} = 3650 \, \text{N} \)
Now, for the power (\(P\)):
\( P_{\text{car}} = F_{\text{car}} \cdot v \)
Substituting the calculated \(F_{\text{total}}\) and the given velocity (\(v = 20 \, \text{m/s}\)):
\( P_{\text{car}} = 3650 \cdot 20 \)
\( P_{\text{car}} = 73000 \, \text{W} \)
So, the power of the car’s engine at the instant when the speed is \(20 \, \text{m/s}\) is \(73000 \, \text{W}\) or \(73 \, \text{kW}\).
Question
Two particles A and B, of masses 0.8 kg and 0.2 kg respectively, are connected by a light inextensible string that passes over a fixed smooth pulley. The particles hang vertically. The system is released from rest. Show that the acceleration of A has magnitude\( 6 m s^{−2}\) and find the tension in the string.
▶️Answer/Explanation
Acceleration of Particle A:
For particle A (mass \(m_A = 0.8 \, \text{kg}\)) hanging vertically:
\[ m_Ag – T = m_Aa \]
Here,
– \(m_Ag\) is the weight of A (downward),
– \(T\) is the tension in the string,
– \(m_Aa\) is the net force acting on A (upward).
Acceleration of Particle B:
For particle B (mass \(m_B = 0.2 \, \text{kg}\)) hanging vertically on the other side of the pulley:
\[ T – m_Bg = m_Ba \]
Here,
– \(T\) is the tension in the string,
– \(m_Bg\) is the weight of B (downward),
– \(m_Ba\) is the net force acting on B (upward).
Equations for Both Particles:
Now, let’s combine the two equations and solve for the acceleration \(a\):
\( m_Ag – T = m_Aa \)
\( T – m_Bg = m_Ba \)
Adding the two equations:
\( (m_A – m_B)g = (m_A + m_B)a \)
Substituting the given values:
\( (0.8 – 0.2) \times 9.8 = (0.8 + 0.2)a \)
Solve for \(a\):
\( 0.6 \times 9.8 = 1a \)
\( a = \frac{0.6 \times 9.8}{1} \)
\( a = 5.88 \, \text{m/s}^2 \)
Tension in the String:
Using the equation for particle A:
\( m_Ag – T = m_Aa \)
Substituting the known values:
\( 0.8 \times 9.8 – T = 0.8 \times 5.88 \)
Solve for \(T\):
\( 7.84 – T = 4.704 \)
\( T = 7.84 – 4.704 \)
\( T = 3.136 \, \text{N} \)
Question
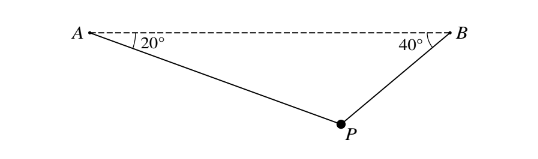
A particle P of mass 1.6 kg is suspended in equilibrium by two light inextensible strings attached to points A and B. The strings make angles of 20Å and 40Å respectively with the horizontal (see diagram).
Find the tensions in the two strings.
▶️Answer/Explanation
\(T_{A} sin 20\) + T_{B} sin 40 = 16
T_{A} cos 20 =\(T_{B}cos40\)
T_{A}=14.2N
T_{B}=17.4N
\(\frac{16}{Sin120}=\frac{T_{B}}{Sin130}\)
\(\frac{16}{Sin120}=\frac{T_{A}}{Sin110}\)
\(T_{A}=14.2N\)
\(T_{B}=17.4N\)