Question
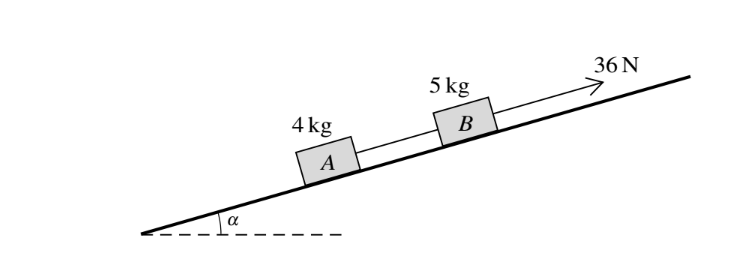
Two blocks A and B of masses 4 kg and 5 kg respectively are joined by a light inextensible string. The
blocks rest on a smooth plane inclined at an angle \(\alpha \)to the horizontal, where\( tan\alpha \frac{7}{24} \).The string is
parallel to a line of greatest slope of the plane with B above A. A force of magnitude 36 N acts on B,
parallel to a line of greatest slope of the plane (see diagram).
(i) Find the acceleration of the blocks and the tension in the string.
(ii) At a particular instant, the speed of the blocks is 1 \(ms^{-1}\). Find the time, after this instant, that it
takes for the blocks to travel 0.65 m.
▶️Answer/Explanation
(i) Acceleration and Tension:
The forces acting on each block are given by Newton’s second law:
For Block A:
\( T – 4 \cdot g \cdot \frac{7}{25} = 4 \cdot a \)
For Block B:
\( 36 – T – 5 \cdot g \cdot \frac{7}{25} = 5 \cdot a \)
Combine the equations for Block A and Block B:
\( 36 – 5 \cdot g \cdot \frac{7}{25} – 4 \cdot g \cdot \frac{7}{25} = 9 \cdot a \)
\( a = 1.2 \ \mathrm{m/s^2} \)
Now, substitute \( a \) back into one of the original equations to find \( T \):
\( T – 4 \cdot g \cdot \frac{7}{25} = 4 \cdot (1.2) \)
\( T = 16 \ \mathrm{N} \)
(ii) Time and Distance:
\( \nu^2 = u^2 + 2 \cdot a \cdot s \)
where:
– \( \nu \) is the final velocity,
– \( u \) is the initial velocity,
– \( a \) is the acceleration,
– \( s \) is the displacement.
In this case, the initial velocity \( u \) is \( 1 \ \mathrm{m/s} \), acceleration \( a \) is \( 1.2 \ \mathrm{m/s^2} \), and displacement \( s \) is \( 0.65 \ \mathrm{m} \).
\( \nu^2 = 1^2 + 2 \cdot 1.2 \cdot 0.65 \)
\( \nu^2 = 1.6 \)
\( \nu = 1.264 \ \mathrm{m/s} \)
Now, to find the time \( t \), use the equation:
\( s = ut + \frac{1}{2} a t^2 \)
Substituting the known values:
\( 0.65 = 1 \cdot t + \frac{1}{2} \cdot 1.2 \cdot t^2 \)
Solve for \( t \):
\( t = 0.5 \ \mathrm{s} \)
So, the time it takes for the blocks to travel \( 0.65 \ \mathrm{m} \) is \( 0.5 \ \mathrm{s} \).
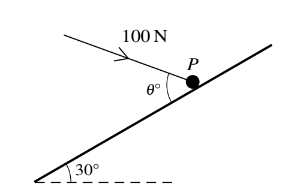
Question
A particle P of mass 8 kg is on a smooth plane inclined at an angle of 30Å to the horizontal. A forceof magnitude 100 N, making an angle of 1Å with a line of greatest slope and lying in the vertical plane containing the line of greatest slope, acts on P (see diagram).
(i) Given that P is in equilibrium, show that 1 = 66.4, correct to 1 decimal place, and find the normal reaction between the plane and P.
(ii) Given instead that 1 = 30, find the acceleration of P.
▶️Answer/Explanation
(i)Calculate \( \theta \)
\( \sin(1) = \frac{8 \cdot 9.8 \cdot \sin(30)}{100} \)
\( \sin(1) = \frac{8 \cdot 9.8 \cdot 0.5}{100} \)
\( \sin(1) = \frac{39.2}{100} \)
\( \theta = \arcsin\left(\frac{39.2}{100}\right) \)
\( \theta \approx 0.651 \ \text{radians} \)
Calculate \( R \):
\( R = 8 \cdot 9.8 \cdot \cos(\theta) \)
\( R = 8 \cdot 9.8 \cdot \cos(0.651) \)
\( R \approx 66.4 \ \text{N} \)
(ii)Calculate \( a \):
\( a = \frac{100 \cdot \sin(30)}{8} \)
\( a = \frac{100 \cdot 0.5}{8} \)
\( a = \frac{50}{8} \)
\( a = 6.25 \ \text{m/s}^2 \)
Question
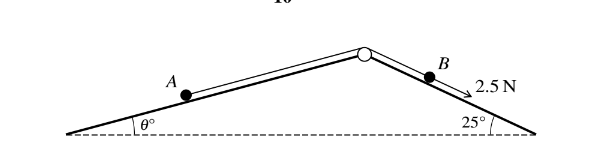
Two particles A and B of masses 0.9 kg and 0.4 kg respectively are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley which is attached to the top of two
inclined planes. The particles are initially at rest with A on a smooth plane inclined at angle \(\Theta ^{\circ}\) to the horizontal and B on a plane inclined at angle \(25 ^{\circ}\) to the horizontal. The string is taut and the particles can move on lines of greatest slope of the two planes. A force of magnitude 2.5 N is applied to B acting down the plane (see diagram).
(i) For the case where 1 = 15 and the plane on which B rests is smooth, find the acceleration of B.
(ii) For a different value of \(\Theta\), the plane on which B rests is rough with coefficient of friction between the plane and B of 0.8. The system is in limiting equilibrium with B on the point of moving in the direction of the 2.5 N force. Find the value of \(\Theta\).
▶️Answer/Explanation
(i)Resolve Forces for Particle \(B\):
– The force \(2.5 \ \mathrm{N}\) applied to \(B\) is resolved into two components:
– \(F_{\parallel} = 2.5 \cdot \sin(25^\circ)\)
– \(F_{\perp} = 2.5 \cdot \cos(25^\circ)\)
Equation of Motion for Particle \(B\):
– Using Newton’s second law to set up the equation of motion for \(B\):
\( F_{\parallel} – T = m \cdot a \)
\( 2.5 \cdot \sin(25^\circ) – T = 0.4 \cdot a \)
Resolve Forces for Particle \(A\):
– The tension \(T\) in the string acts on \(A\) in the opposite direction:
\( T – 0.9 \cdot g \cdot \sin(15^\circ) = 0.9 \cdot a \)
Solve for Acceleration (\(a\)):
– Solve the system of equations to find \(a\):
\( 2.5 \cdot \sin(25^\circ) – T = 0.4 \cdot a \)
\( T – 0.9 \cdot g \cdot \sin(15^\circ) = 0.9 \cdot a \)
\(a \approx 1.43 \ \mathrm{m/s^2}\).
(ii)Frictional Force (\(F_{\text{friction}})\):
– Given that the plane on which \(B\) rests is rough with a coefficient of friction \(\mu = 0.8\):
\( F_{\text{friction}} = \mu \cdot R = 0.8 \cdot 0.4 \cdot g \cdot \cos(25^\circ) \)
Equation of Motion for Particle \(B\) in Limiting Equilibrium:
– Set up the equation of motion for \(B\) in the direction of the force \(2.5 \ \mathrm{N}\):
\( 2.5 + 0.4 \cdot g \cdot \sin(25^\circ) – T – F_{\text{friction}} = 0 \)
Expression for Normal Reaction (\(R\)):
– The normal reaction (\(R\)) is related to the weight component perpendicular to the plane:
\( R = mg \cdot \cos(\Theta) \)
Equation in Limiting Equilibrium:
– Use the equation \(T – 0.9 \cdot g \cdot \sin(\Theta) = 0\) for equilibrium:
\( T – 0.9 \cdot g \cdot \sin(\Theta) = 0 \)
Solve for \(\Theta\):
– Substitute the expressions for \(T\), \(F_{\text{friction}}\), and \(R\) into the equation in limiting equilibrium:
\( 2.5 + 0.4 \cdot g \cdot \sin(25^\circ) – T – F_{\text{friction}} = 0 \)
\(\Theta \approx 8.20^\circ\).
Question
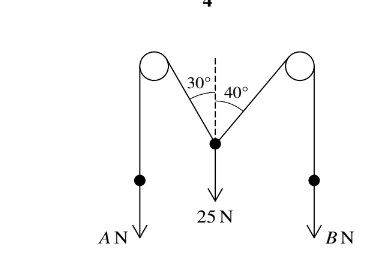
Two light inextensible strings are attached to a particle of weight 25 N. The strings pass over two smooth fixed pulleys and have particles of weights A N and B N hanging vertically at their ends. The
sloping parts of the strings make angles of 30Å and 40Å respectively with the vertical (see diagram). The system is in equilibrium. Find the values of A and B.
▶️Answer/Explanation
Conditions for Equilibrium:
Vertical Forces: The sum of the vertical components of the forces must be zero.
\( A \cos 30^\circ + B \cos 40^\circ = 25 \ \mathrm{N} \)
Horizontal Forces:The sum of the horizontal components of the forces must be zero.
\( A \sin 30^\circ – B \sin 40^\circ = 0 \)
Torque Condition:
The torque due to the forces acting on the particle must be zero. The torque is calculated as the force multiplied by the perpendicular distance from the pivot point.
\( A \sin 30^\circ \cdot d – B \sin 40^\circ \cdot d = 0 \)
Expressions for \(A\) and \(B\):
From the Vertical Forces equation:
\( A = \frac{25}{\cos 30^\circ} \)
Substitute \(A\) into the Horizontal Forces equation:
\( \frac{25}{\cos 30^\circ} \sin 30^\circ – B \sin 40^\circ = 0 \)
Solve for \(B\) in terms of \(A\):
\( B = \frac{25 \cdot \sin 30^\circ}{\sin 40^\circ \cdot \cos 30^\circ} \)
Substituting the values:
\( A = 17.1 \ \mathrm{N} \)
\( B = 13.3 \ \mathrm{N} \)
Alternatively, you can use trigonometric ratios directly:
\( \frac{25}{\sin 70^\circ} = \frac{A}{\sin 140^\circ} = \frac{B}{\sin 150^\circ} \)
Solving for \(B\):
\( B = \frac{25 \cdot \sin 150^\circ}{\sin 70^\circ} = 13.3 \ \mathrm{N} \)
Question
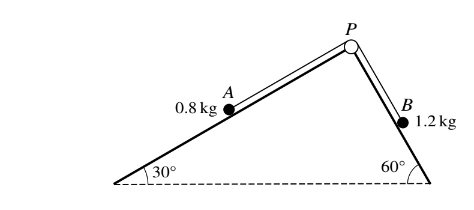
As shown in the diagram, a particle A of mass 0.8 kg lies on a plane inclined at an angle of 30Å to the horizontal and a particle B of mass 1.2 kg lies on a plane inclined at an angle of 60Å to the horizontal. The particles are connected by a light inextensible string which passes over a small smooth pulley P fixed at the top of the planes. The parts AP and BP of the string are parallel to lines of greatest slope of the respective planes. The particles are released from rest with both parts of the string taut.
(i) Given that both planes are smooth, find the acceleration of A and the tension in the string.
(ii) It is given instead that both planes are rough, with the same coefficient of friction, -, for both particles. Find the value of – for which the system is in limiting equilibrium.
▶️Answer/Explanation
(i) Smooth Planes:
For Particle A:
– The forces acting on A are its weight (\(0.8 \, \mathrm{kg} \times 9.8 \, \mathrm{m/s^2}\)) along the slope and tension (\(T\)) in the string opposite to the weight.
– Using Newton’s second law (\(\sum F = m \cdot a\)) along the slope, we get:
\( T – 0.8 \cdot 9.8 \cdot \sin(30^\circ) = 0.8 \cdot a \)
For Particle B:
– The forces acting on B are its weight (\(1.2 \, \mathrm{kg} \times 9.8 \, \mathrm{m/s^2}\)) along the slope and tension (\(T\)) in the string along the slope.
– Using Newton’s second law along the slope, we get:
\( 1.2 \cdot 9.8 \cdot \sin(60^\circ) – T = 1.2 \cdot a \)
System of Equations:
– The equations for A and B form a system:
\( T – 0.8 \cdot 9.8 \cdot \sin(30^\circ) = 0.8 \cdot a \)
\( 1.2 \cdot 9.8 \cdot \sin(60^\circ) – T = 1.2 \cdot a \)
Solve for Acceleration (\(a\)) and Tension (\(T\)):
– Solving these equations gives \(a = 3.20 \, \mathrm{m/s^2}\) and \(T = 6.56 \, \mathrm{N}\).
(ii) Rough Planes:
Forces on Particle A:
– The normal reaction (\(R_A\)) is equal to the component of the weight perpendicular to the slope.
\( R_A = 0.8 \cdot \cos(30^\circ) \)
– The frictional force (\(F_A\)) opposes the motion and is given by \(F_A = \mu \cdot R_A\).
Forces on Particle B:
– Similar to A, the normal reaction (\(R_B\)) is equal to the component of the weight perpendicular to the slope.
\( R_B = 1.2 \cdot \cos(60^\circ) \)
– The frictional force (\(F_B\)) opposes the motion and is given by \(F_B = \mu \cdot R_B\).
Equations for Equilibrium:
– The equilibrium equations for A and B are:
\( 12 \cdot \sin(60^\circ) – F_B – T = 0 \)
\( T – 8 \cdot \sin(30^\circ) – F_A = 0 \)
Solve for Coefficient of Friction (\(\mu\)):
– The coefficient of friction (\(\mu\)) is found by solving these equations.
– Solving gives \(\mu = 0.494\).
Question
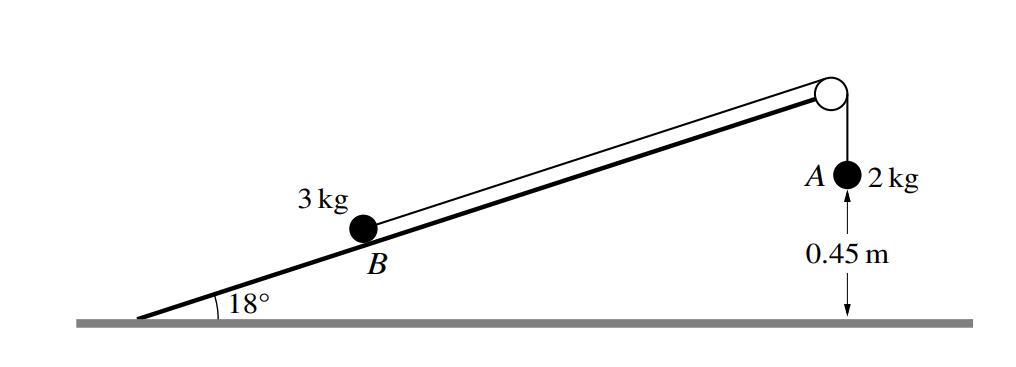
Two particles A and B of masses 2 kg and 3 kg respectively are connected by a light inextensible string. Particle B is on a smooth fixed plane which is at an angle of 180 to horizontal ground. The string passes over a fixed smooth pulley at the top of the plane. Particle A hangs vertically below the pulley and is 0.45 m above the ground (see diagram). The system is released from rest with the string taut. When A reaches the ground, the string breaks.
Find the total distance travelled by B before coming to instantaneous rest. You may assume that B does not reach the pulley.
▶️Answer/Explanation
Given:
– Particle A mass, \(m_A = 2 \, \mathrm{kg}\)
– Particle B mass, \(m_B = 3 \, \mathrm{kg}\)
– Distance between particle A and the ground, \(h = 0.45 \, \mathrm{m}\)
– Angle of the plane, \(\theta = 18^\circ\)
– Particle A is hanging vertically below the pulley, and particle B is on a smooth inclined plane.
– The system is released from rest, and the string is taut.
– For Particle A: Using Newton’s second law, \(m_Ag – T = m_Aa\), where \(a\) is the acceleration.
– For Particle B: Using Newton’s second law along the incline, \(T – m_Bg \sin(\theta) = m_Ba\).
– Considering the system, the net force is \(m_Ag – m_Bg \sin(\theta)\), leading to \(m_Ag – m_Bg \sin(\theta) = (m_A + m_B)a\).
Solving for Acceleration:
– Substituting the known values, you find \(a \approx 2.1459 \, \mathrm{m/s^2}\).
Calculating Final Velocity of Particle A:
– Using the kinematic equation \(v^2 = u^2 + 2as\), where \(u = 0\) (initial velocity), \(a\) is the acceleration, and \(s\) is the distance traveled by particle A.
– \(v^2 = 2 \times a \times h\), resulting in \(v \approx 1.3897 \, \mathrm{m/s}\).
Analyzing Tension in the String:
– The tension in the string when A reaches the ground (\(T\)) can be found by considering the forces on B.
– \(T – m_Bg \sin(\theta) = 0\) at the moment A reaches the ground, leading to \(T = m_Bg \sin(\theta)\).
Determining Acceleration of Particle B after String Breaks:
– After the string breaks, particle B experiences free fall along the inclined plane.
– The acceleration becomes \(g \sin(\theta)\), leading to \(a = 3.09 \, \mathrm{m/s^2}\).
Calculating Time of Flight for Particle B:
– Using the kinematic equation \(v = u + at\) for B, where \(u = 0\) (initial velocity after the string breaks), \(a\) is the acceleration, and \(t\) is the time of flight.
– \(1.93 – 2 \times 3.09 \times t = 0\), resulting in \(t \approx 0.312 \, \mathrm{s}\).
Total Distance Moved by Particle B:
– The total distance is the sum of the initial distance from the top (\(h\)) and the distance traveled after the string breaks (\(0.312 \, \mathrm{m}\)).
– Total distance = \(h + 0.312 \, \mathrm{m} = 0.762 \, \mathrm{m}\).
Question
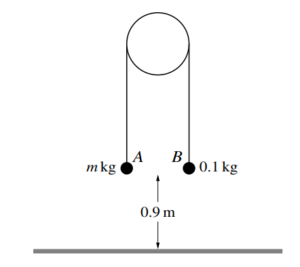
Two particles A and B have masses m kg and 0.1 kg respectively, where m > 0.1. The particles are
attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley and
the particles hang vertically below it. Both particles are at a height of 0.9 m above horizontal ground
(see diagram). The system is released from rest, and while both particles are in motion the tension in
the string is 1.5 N. Particle B does not reach the pulley.
(a) Find m.
(b) Find the speed at which A reaches the ground.
▶️Answer/Explanation
Given
– Mass of particle B, \(m\) kg
– Mass of particle A, \(0.1 \, \mathrm{kg}\)
– Tension in the string, \(T = 1.5 \, \mathrm{N}\)
– Both particles are at a height of \(0.9 \, \mathrm{m}\) above the ground
– Particle B does not reach the pulley
(a) To find \(m\):
Considering the forces on particle B:
\( mg – T = ma \)
\( mg – 0.1g = (m + 0.1) a \)
Since both particles are in motion, we can use the acceleration \(a\) as \(g\), where \(g\) is the acceleration due to gravity (\(9.8 \, \mathrm{m/s^2}\)):
\( mg – 0.1g = (m + 0.1) g \)
\( m – 0.1 = m + 0.1 \)
\( 0.1 = 0.1m \)
\( m = 1 \, \mathrm{kg} \)
(b) To find the speed at which A reaches the ground:
For particle A, using \(a = g\):
\( mg – T = ma \)
\( mg – 1.5 = m \times g \)
Solving for \(g\):
\( 1.5 = g \)
\( g = 1.5 \, \mathrm{m/s^2} \)
Now, using the kinematic equation \(v^2 = u^2 + 2as\), where \(u\) is the initial velocity (which is \(0\) as it is released from rest), \(a\) is acceleration, and \(s\) is the distance:
\( v^2 = 0 + 2 \times 1.5 \times 0.9 \)
\( v = \sqrt{2 \times 1.5 \times 0.9} \)
\( v = 3 \, \mathrm{m/s} \)
Question
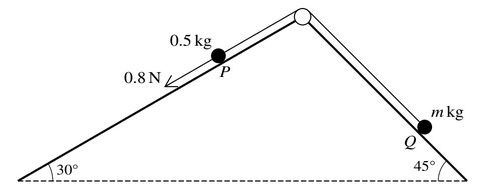
Two particles P and Q of masses 0.5 kg and m kg respectively are attached to the ends of a light
inextensible string. The string passes over a fixed smooth pulley which is attached to the top of two
inclined planes. The particles are initially at rest with P on a smooth plane inclined at 30Å to the
horizontal and Q on a plane inclined at 45Å to the horizontal. The string is taut and the particles can
move on lines of greatest slope of the two planes. A force of magnitude 0.8 N is applied to P acting
down the plane, causing P to move down the plane (see diagram).
(a) It is given that m = 0.3, and that the plane on which Q rests is smooth.
Find the tension in the string.
(b) It is given instead that the plane on which Q rests is rough, and that after each particle has moved a distance of 1m, their speed is 0.6ms^{-1}\). The work done against friction in this part of the motion is 0.5 J.
▶️Answer/Explanation
- Attempt Newton’s 2nd law for either P, Q or the system.
For P: 0.8+0.5g sin 30 – T = 0.5a
For Q: T-0.3g sin 45=0.3a
System: 0.8+0.5g sin 30-0.3g sin 45 = 0.8a
Attempt to solve for T.
T=2.56 N (3sf) - KE and PE for m kg particle:
\(\frac{1}{2}m \times 0.36=0.18m\) and \(mg sin 45=5\sqrt{2}m\)
KE and PE for 0.5 kg particle:
\(\frac{1}{2} \times 0.5 \times 0.36 = 0.09 \) and 0.5g sin 30 = 2.5
Apply the work-energy equation to the system as:
PE loss + WD by 0.8N = KE gain +0.5
\(0.5g\times 1 \times sin 30-mg \times 1 \times sin 45 + 0.8 \times 1\)
m=0.374Alternative method for question 7(b)
KE and PE for m kg particle:
\(\frac{1}{2}m\times 0.36=0.18m\) and \(mg sin 45 = 5\sqrt{2}m\)
a = 0.18 and 3.3 – T =0.5(0.18) leading to T = 3.21
For m kg particle:
WD by T=KE gain + PE gain + 0.5
\(3.21\times1=\frac{1}{2}m \times 0.36 + mg sin 45+ 0.5\)
m=0.374Alternative method for question 7(b)
KE and PE for m kg particle:
\(\frac{1}{2}m \times 0.36=0.18m\) and mg sin 45 =\(5\sqrt{2}m\)
KE and PE for 0.5 kg particle
\(\frac{1}{2}\times 0.5 \times 0.36 = 0.09\) and 0.5g sin 30 = 2.5
Apply the work-energy equation to both particles as;
\(0.8\times 1+0.5gsin30=\frac{1}{2}\times0.5\times 0.36+T \times 1\)
and \(T\times 1=\frac{1}{2}m \times 0.36 + mg sin 45+0.5\)
\(0.8\times 1+0.5gsin30-\frac{1}{2}\times 0.5 \times 0.36=\frac{1}{2}m \times 0.36 + mg sin 45+0.5\)
m = 0.374
Question
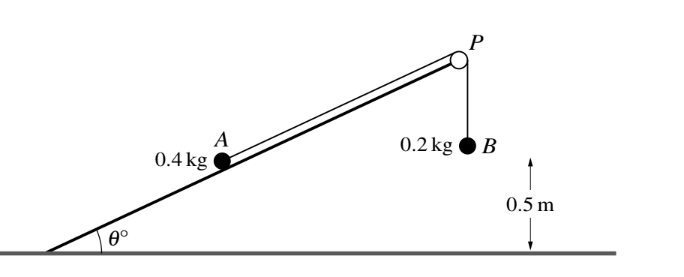
Two particles A and B, of masses 0.4 kg and 0.2 kg respectively, are connected by a light inextensible
string. Particle A is held on a smooth plane inclined at an angle of 1Å to the horizontal. The string passes over a small smooth pulley P fixed at the top of the plane, and B hangs freely 0.5 m above horizontal ground (see diagram). The particles are released from rest with both sections of the string
taut.
(i) Given that the system is in equilibrium, find 1.
(ii) It is given instead that 1 = 20. In the subsequent motion particle A does not reach P and B remains at rest after reaching the ground. Find the tension in the string and the acceleration of the system.
▶️Answer/Explanation
Given:
– Mass of particle A (\(m_A\)) = 0.4 kg
– Mass of particle B (\(m_B\)) = 0.2 kg
– Angle of the incline (\(\theta\)) = 20 degrees
– Particle A is held on a smooth inclined plane.
– Particle B hangs freely.
Equations of Motion:
For particle A (on the inclined plane):
\( T = m_A \cdot g \cdot \sin(\theta) \)
Here, \(T\) is the tension in the string.
For particle B (hanging freely):
\( T = m_B \cdot g \)
\(T\) is also the tension in the string.
Equations for Equilibrium:
1. For particle A:
\( T – m_A \cdot g \cdot \sin(20) = 0 \)
This equation ensures that the forces in the direction perpendicular to the incline are balanced.
2. For particle B:
\( 2 – T – m_B \cdot g = 0 \)
This equation ensures that the forces acting on particle B (weight and tension) are balanced.
System of Equations:
The system of equations to solve simultaneously:
\( T – 4 \sin(20) = 0.4 \cdot a \)
\( 2 – T = 0.2 \cdot a \)
Solving the System:
Substituting the expression for \(T\) from equation (1) into equation (2):
\( 2 – (m_A \cdot g \cdot \sin(\theta)) = 0.2 \cdot a \)
Substituting the values:
\( 2 – (0.4 \cdot 9.8 \cdot \sin(20)) = 0.2 \cdot a \)
Solving for \(a\):
\( a \approx 1.05 \, \text{m/s}^2 \)
Substituting the value of \(a\) into equation (1) to find \(T\):
\( T – 4 \sin(20) = 0.4 \cdot a \)
\( T – 4 \sin(20) = 0.4 \cdot 1.05 \)
Solve for \(T\):
\( T \approx 1.79 \, \text{N} \)
So, the system is in equilibrium with a tension in the string (\(T\)) of approximately 1.79 N and a common acceleration (\(a\)) of approximately 1.05 m/s².
Question
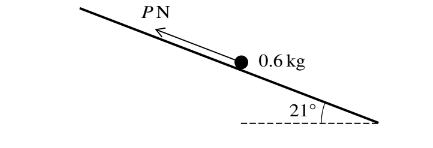
A particle of mass 0.6 kg is placed on a rough plane which is inclined at an angle of 21Å to the
horizontal. The particle is kept in equilibrium by a force of magnitude P N acting parallel to a line of
greatest slope of the plane, as shown in the diagram. The coefficient of friction between the particle
and the plane is 0.3. Show that the least possible value of P is 0.470, correct to 3 significant figures, and find the greatest possible value of P.
▶️Answer/Explanation
The forces acting on the particle are its weight (\(mg\)), the normal reaction (\(R\)), and the frictional force (\(F\)).
Normal Reaction (\(R\)):
The normal reaction is the component of the weight perpendicular to the plane.
\( R = mg \cos(\theta) \) where \( \theta \) is the angle of inclination.
Substituting the given values:
\( R = 0.6 \times 9.8 \times \cos(21^\circ) \approx 5.60 \, \text{N} \)
Frictional Force (\(F\)):
The frictional force is given by \( F = \mu R \), where \( \mu \) is the coefficient of friction.
\( F = 0.3 \times R \)
Substituting the value of \( R \):
\( F = 0.3 \times 5.60 \approx 1.68 \, \text{N} \)
Resultant Force (\(P\)):
The force \( P \) is acting parallel to the line of greatest slope. The equilibrium equation in the direction of \( P \) is:
\( P + F = mg \sin(\theta) \)
\( P + 1.68 = 0.6 \times 9.8 \times \sin(21^\circ) \)
\( P \approx 2.15 – 1.68 \approx 0.470 \, \text{N} \)
Therefore, the least possible value of \( P \) is approximately 0.470 N.
Greatest Possible Value of \( P \):
The greatest possible value of \( P \) occurs when the friction force is in the opposite direction to \( P \), so the equation becomes:
\( P – F = mg \sin(\theta) \)
\( P – 1.68 = 0.6 \times 9.8 \times \sin(21^\circ) \)
\( P \approx 2.15 + 1.68 \approx 3.83 \, \text{N} \)
Therefore, the greatest possible value of \( P \) is approximately 3.83 N.
Question

Two particles P and Q, of masses 0.6 kg and 0.4 kg respectively, are connected by a light inextensible string. The string passes over a small smooth light pulley fixed at the edge of a smooth horizontal table. Initially P is held at rest on the table and Q hangs vertically (see diagram). P is then released. Find the tension in the string and the acceleration of Q
▶️Answer/Explanation
Given:
– Mass of particle P (\(m_P\)) = 0.6 kg
– Mass of particle Q (\(m_Q\)) = 0.4 kg
– Acceleration due to gravity (\(g\)) = 9.8 m/s²
The forces acting on particle P are:
Tension in the string (\(T\)) acting upward.
Weight of P (\(m_P \cdot g\)) acting downward.
Normal force (\(N\)) from the table acting upward.
Friction (\(f\)) acting horizontally and opposite to the direction of motion.
The forces acting on particle Q are:
Weight of Q (\(m_Q \cdot g\)) acting downward.
Tension in the string (\(T\)) acting upward.
Since particle P is on a smooth horizontal table, there is no friction (\(f = 0\)). Therefore, the net force on P is given by:
\( T = m_P \cdot a \)
\( T = 0.6a \)
For particle Q, the net force is given by:
\( m_Q \cdot g – T = m_Q \cdot a \)
\( 0.4 \cdot 9.8 – T = 0.4a \)
\( 3.92 – T = 0.4a \)
Now, we have a system of two equations:
\( T = 0.6a \) (Equation 1)
\( 3.92 – T = 0.4a \) (Equation 2)
We can solve this system to find the values of \(T\) and \(a\).
Substitute Equation 1 into Equation 2:
\( 3.92 – (0.6a) = 0.4a \)
Combine like terms:
\( 3.92 – 0.6a = 0.4a \)
\( 0.4a + 0.6a = 3.92 \)
\( 1a = 3.92 \)
\( a = 3.92 \, \text{m/s}^2 \)
Now, substituting the value of \(a\) back into Equation 1 to find \(T\):
\( T = 0.6 \cdot 3.92 \)
\( T = 2.352 \, \text{N} \)
So, the tension in the string is \(2.352 \, \text{N}\) and the acceleration of particle Q is \(3.92 \, \text{m/s}^2\).
Question
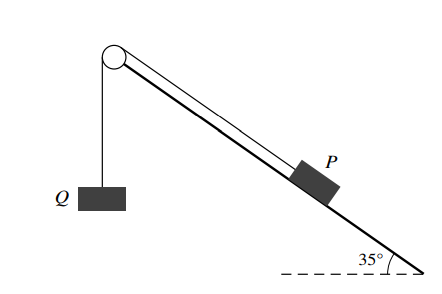
Blocks P and Q, of mass m kg and 5 kg respectively, are attached to the ends of a light inextensible string. The string passes over a small smooth pulley which is fixed at the top of a rough plane inclined at 35° to the horizontal. Block P is at rest on the plane and block Q hangs vertically below the pulley (see diagram). The coefficient of friction between block P and the plane is 0.2. Find the set of values of m for which the two blocks remain at rest.
▶️Answer/Explanation
Given:
– Mass of block \(P\): \(m\) kg
– Mass of block \(Q\): \(5\) kg
– Incline angle: \(\theta = 35^\circ\)
– Coefficient of friction between block \(P\) and the incline: \(\mu = 0.2\)
We want to find the set of values of \(m\) for which the two blocks remain at rest. In this scenario, the system is in equilibrium, so the net force acting on each block is zero.
Let’s analyze the forces acting on block \(P\):
Tension (\(T\)): This force pulls block \(P\) up the incline.
Gravity (\(mg\)):The component along the incline is \(mg \sin \theta\).
Normal force (\(N\)): Acting perpendicular to the incline.
Frictional force (\(\mu N\)): Opposing the motion.
Now, let’s write the equations of motion for block \(P\):
Along the incline (\(x\)-axis):
\(T – \mu N = 0\)
Perpendicular to the incline (\(y\)-axis):
\(N – mg \sin \theta = 0\)
For block \(Q\), the only force acting is its weight (\(5g\)), and the net force along the \(y\)-axis is:
\(T – 5g = 0\)
Now, we can solve these equations. First, solve for \(N\) using the second equation:
\(N = mg \sin \theta\)
Now, substitute \(N\) into the first equation to find \(T\):
\(T – \mu N = T – \mu mg \sin \theta = 0 \implies T = \mu mg \sin \theta\)
Substitute this \(T\) into the equation for block \(Q\):
\(\mu mg \sin \theta – 5g = 0 \implies \mu \sin \theta = \frac{5}{m}\)
Now, substitute the given values for \(\mu\) and \(\theta\), and solve for \(m\):
\(\sin 35^\circ \times 0.2 = \frac{5}{m} \implies m = \frac{5}{\sin 35^\circ \times 0.2} \approx 12.2\)
So, the set of values for \(m\) for which the two blocks remain at rest is \(6.78 \leq m \leq 12.2\).
Question

Particles A and B, of masses 0.3 kg and 0.7 kg respectively, are attached to the ends of a light inextensible string. Particle A is held at rest on a rough horizontal table with the string passing over a smooth pulley fixed at the edge of the table. The coefficient of friction between A and the table is 0.2. Particle B hangs vertically below the pulley at a height of 0.5 m above the floor (see diagram). The system is released from rest and 0.25 s later the string breaks. A does not reach the pulley in the subsequent motion. Find
(i) the speed of B immediately before it hits the floor,
(ii) the total distance travelled by A.
▶️Answer/Explanation
(i)Equations of motion for A and B before the string breaks:
– For A: \(T – 0.2 \times 3 = 0.3a\)
– For B: \(7 – T = 0.7a\)
Solving for acceleration:
– Acceleration \(a = 6.4 \, \mathrm{ms^{-2}}\)
Calculating the speed of B just before it hits the floor:
– Initial velocity \(u = 0\)
– Time \(t = 0.25 \, \mathrm{s}\)
– Using \(v = u + at\),
\(v=0+6.4\times 0.25\)
\(v = 1.6 \, \mathrm{ms^{-1}}\)
Calculating the distance traveled by A before the string breaks:
– Using \(s = ut + \frac{1}{2}at^2\),
\(s=0+\frac{1}{2}\times 6.4\times 0.25^{2}\)
\(s = 0.2 \, \mathrm{m}\)
Calculating the final speed of B:
– Using the work-energy principle, \(v^2 = u^2 + 2as\),
\(v^2=1.6^2+2 g \times(0.5-0.2)\)
v= \(2.93 \, \mathrm{ms^{-1}}\)
Part (ii)Calculating the distance traveled by A after the string breaks:
=\(\frac{0-1.6^{2}}{2\times -2}\)
=0.64
Calculating the total distance traveled by A:
The total distance is the sum of the distance traveled before and after the string breaks=0.2+0.64=0.84
Calculating the work done (WD) during and after the break:
– Tension \(T = 2.52 \, \mathrm{N}\), Frictional force \(F = 0.2 \times 3\)
– Work done by Tension: \(WD_T = 2.52 \times 0.2\)
– Work done by Friction: \(WD_F = 0.2 \times 3 \times d\)
Solving for the distance \(d\):
\(0.6d = 2.52 \times 0.2\),
\(d = 0.84 \, \mathrm{m}\)
Question
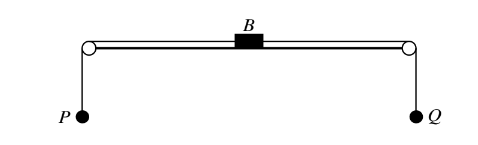
A small block B of mass 0.25 kg is attached to the mid-point of a light inextensible string. Particles P and Q, of masses 0.2 kg and 0.3 kg respectively, are attached to the ends of the string. The string passes over two smooth pulleys fixed at opposite sides of a rough table, with B resting in limiting equilibrium on the table between the pulleys and particles P and Q and block B are in the same vertical plane (see diagram).
(i) Find the coefficient of friction between B and the table. Q is now removed so that P and B begin to move.
(ii) Find the acceleration of P and the tension in the part PB of the string.
▶️Answer/Explanation
(i)Finding the Coefficient of Friction (\(\mu\)):
The frictional force (\(f\)) is given by \(f = \mu \cdot \mathrm{Normal~Force}\). In this case, the normal force is the weight of block B, which is \(0.25 \, \mathrm{kg} \times g\).
So, \( f = \mu \cdot 0.25 \, \mathrm{kg} \times g \)
The system is in equilibrium, which means the sum of forces is zero. The forces acting on block B are its weight and the frictional force.
\( \sum F_y = 0 \implies 0.3 \, \mathrm{kg} \cdot g = 0.2 \, \mathrm{kg} \cdot g + \mu \cdot 0.25 \, \mathrm{kg} \cdot g \)
Now, solve for \(\mu\):
\( 0.3g = 0.2g + \mu \cdot 0.25g \)
\( 0.1g = \mu \cdot 0.25g \)
\( \mu = \frac{0.1}{0.25} = 0.4 \)
So, the coefficient of friction between block B and the table is \(0.4\).
(ii) Acceleration and Tension in Segment \(\overline{PB}\):
For particle \(P\):
\(0.2 \mathrm{~g} – \mathrm{T} = 0.2a\)
For block \(B\):
\(\mathrm{T} – 0.4 \times 0.25 \mathrm{~g} = 0.25a\)
Now, substitute the given values and solve for acceleration and tension:
For the first equation:
\(0.2 \times 9.8 – \mathrm{T} = 0.2a\)
\(1.96 – \mathrm{T} = 0.2a\)
\(0.2a = 1.96 – \mathrm{T}\)
For the second equation:
\(\mathrm{T} – 0.4 \times 0.25 \times 9.8 = 0.25a\)
\(0.4 \times 0.25 \times 9.8 = \mathrm{T} – 0.25a\)
\(0.98 = \mathrm{T} – 0.25a\)
Now, substitute the value of \(0.2a\) from the first equation into the second:
\(0.2a = 1.96 – \mathrm{T}\)
\(0.98 = \mathrm{T} – 0.25a\)
Combine these equations:
\(0.98 = (1.96 – \mathrm{T}) – 0.25a\)
\(0.98 = 1.96 – \mathrm{T} – 0.25a\)
\(0.98 = 1.96 – (0.2a) – 0.25a\)
Combine like terms:
\(0.98 = 1.96 – 0.45a\)
Solve for \(a\):
\(0.45a = 1.96 – 0.98\)
\(0.45a = 0.98\)
\(a = \frac{0.98}{0.45} \approx 2.18 \mathrm{~m/s^2}\)
Now, substitute the value of \(a\) back into any of the original equations to find \(\mathrm{T}\). Let’s use the first equation:
\(0.2a = 1.96 – \mathrm{T}\)
\(0.2 \times 2.18 = 1.96 – \mathrm{T}\)
\(0.436 = 1.96 – \mathrm{T}\)
\(\mathrm{T} = 1.96 – 0.436\)
\(\mathrm{T} \approx 1.52 \mathrm{~N}\)
So, the values are: \(a \approx 2.18 \mathrm{~m/s^2}\) and \(\mathrm{T} \approx 1.52 \mathrm{~N}\).
Question
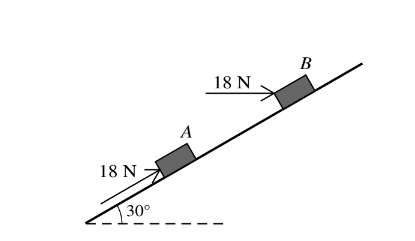
Small blocks A and B are held at rest on a smooth plane inclined at 30Å to the horizontal. Each is held in equilibrium by a force of magnitude 18 N. The force on A acts upwards parallel to a line of greatest slope of the plane, and the force on B acts horizontally in the vertical plane containing a line of greatest slope (see diagram). Find the weight of A and the weight of B.
▶️Answer/Explanation
For Block A:
– The force \(18 \, \text{N}\) is acting upwards at an angle of \(30^{\circ}\) to the horizontal.
– The weight (\(W_A\)) is acting vertically downward.
Equation for Block A:
\( W_A \sin(30^{\circ}) = 18 \, \text{N} \)
\( W_A = \frac{18 \, \text{N}}{\sin(30^{\circ})} \)
\( W_A \approx \frac{18 \, \text{N}}{0.5} \)
\( W_A \approx 36 \, \text{N} \)
So, the weight of Block A is approximately \(36 \, \text{N}\).
For Block B:
– The force \(18 \, \text{N}\) is acting horizontally.
– The weight (\(W_B\)) is acting vertically downward at an angle of \(30^{\circ}\) to the horizontal.
Equation for Block B:
\( W_B \sin(30^{\circ}) = 18 \, \text{N} \cos(30^{\circ}) \)
\( W_B = \frac{18 \, \text{N} \cos(30^{\circ})}{\sin(30^{\circ})} \)
\( W_B \approx \frac{18 \, \text{N} \times \frac{\sqrt{3}}{2}}{0.5} \)
\( W_B \approx 31.2 \, \text{N} \)
So, the weight of Block B is approximately \(31.2 \, \text{N}\).
Question
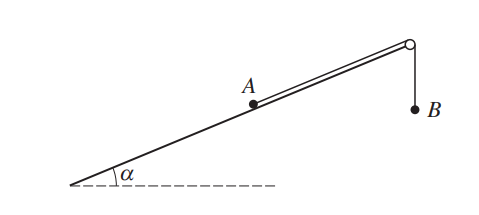
A light inextensible string has a particle A of mass 0.26 kg attached to one end and a particle B of mass 0.54 kg attached to the other end. The particle A is held at rest on a rough plane inclined at angle α to the horizontal, where sin \(\alpha =\frac{5}{13}\). The string is taut and parallel to a line of greatest slope of the plane. The string passes over a small smooth pulley at the top of the plane. Particle B hangs at rest vertically below the pulley (see diagram). The coefficient of friction between A and the plane is 0.2. Particle A is released and the particles start to move.
(i) Find the magnitude of the acceleration of the particles and the tension in the string.
Particle A reaches the pulley 0.4 s after starting to move.
(ii) Find the distance moved by each of the particles.
▶️Answer/Explanation
(i) Magnitude of Acceleration and Tension:
Given that particle A reaches the pulley \(0.4 \, \text{s}\) after starting to move, we can use the equations of motion for the two particles.
For particle A:
\( R = m_A \cdot g \cdot \sin(\alpha) \)
\( R = 0.26 \cdot 9.8 \cdot \frac{5}{13} \)
\( R \approx 2.4 \, \text{N} \)
The frictional force \(F\) is given by \(F = \mu \cdot R\), where \(\mu\) is the coefficient of friction (0.2 in this case).
\( F = 0.2 \cdot 2.4 \)
\( F = 0.48 \, \text{N} \)
Now, applying Newton’s second law to A:
\( T – m_A \cdot g \cdot \sin(\alpha) – F = m_A \cdot a \)
\( T – 0.26 \cdot 9.8 \cdot \frac{5}{13} – 0.48 = 0.26 \cdot a \)
\( T – 5.4 – 0.48 = 0.26 \cdot a \)
\( T = 0.26 \cdot a + 5.88 \)
For particle B:
\( T – m_B \cdot g = m_B \cdot a \)
\( T – 0.54 \cdot 9.8 = 0.54 \cdot a \)
\( T = 0.54 \cdot a + 5.292 \)
Now, we have two equations involving \(T\) and \(a\):
\( 0.26 \cdot a + 5.88 = 2.6 \cdot \left(\frac{5}{13}\right) + 0.2 \cdot 2.4 \)
\( 0.54 \cdot a + 5.292 = 5.4 \)
Solving these equations simultaneously, we get:
\( a \approx 4.9 \, \text{m/s}^2 \)
\( T \approx 2.75 \, \text{N} \)
(ii) Distance Moved by Each Particle:
For particle A:
\( s_A = \frac{1}{2} a t^2 \)
\( s_A = \frac{1}{2} \cdot 4.9 \cdot (0.4)^2 \)
\( s_A = \frac{1}{2} \cdot 4.9 \cdot 0.16 \)
\( s_A = 0.392 \, \text{m} \)
Question
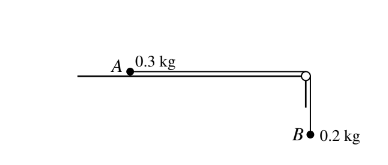
Particles A and B, of masses 0.3 kg and 0.2 kg respectively, are attached to the ends of a light inextensible string. A is held at rest on a rough horizontal table with the string passing over a small smooth pulley at the edge of the table. B hangs vertically below the pulley (see diagram). The system is released and B starts to move downwards with acceleration 1.6 m\( s^{−2}\). Find
(i) the tension in the string after the system is released,
(ii) the frictional force acting on A.
▶️Answer/Explanation
(i) Tension in the String:
\( 0.2 \cdot g – T = 0.2 \cdot a \)
\( 1.96 – T = 0.32 \)
\( T = 1.68 \, \text{N} \)
(ii) Frictional Force on A:
\( T – F = m_A \cdot a \)
\( 1.68 – F = 0.3 \cdot 1.6 \)
\( F = 1.2 \, \text{N} \)
Question
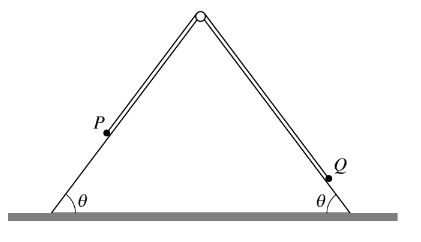
Particles P and Q, of masses 0.6 kg and 0.4 kg respectively, are attached to the ends of a light inextensible string. The string passes over a small smooth pulley which is fixed at the top of a vertical
cross-section of a triangular prism. The base of the prism is fixed on horizontal ground and each of the sloping sides is smooth. Each sloping side makes an angle θ with the ground, where sin θ = 0.8.
Initially the particles are held at rest on the sloping sides, with the string taut (see diagram). The
particles are released and move along lines of greatest slope.
(i) Find the tension in the string and the acceleration of the particles while both are moving.
The speed of P when it reaches the ground is 2 \(ms{−1}\). On reaching the ground P comes to rest and remains at rest. Q continues to move up the slope but does not reach the pulley.
(ii) Find the time taken from the instant that the particles are released until Q reaches its greatest
height above the ground.
▶️Answer/Explanation
(i) Tension in the string and acceleration:
Given equations:
\( 0.6 \, g \times 0.8 – T = 0.6a \)
\( T – 0.4 \, g \times 0.8 = 0.4a \)
1. \( 0.48 – T = 0.6a \)
2. \( T – 0.32 = 0.4a \)
Adding these equations:
\( (0.48 – T) + (T – 0.32) = 0.6a + 0.4a \)
\( 0.16 = a \)
Now, calculate the tension \(T\):
\( 0.48 – T = 0.6 \times 0.16 \)
\( 0.48 – T = 0.096 \)
\( T = 0.48 – 0.096 \)
\( T = 0.384 \, \text{N} \)
So, the correct tension is \(0.384 \, \text{N}\).
(ii)Time taken for Q to reach its greatest height:
Given equations:
\( 2 = 1.6 \, t_1 \)
\( 0 = 2 – 0.8 \, g \, t_2 \)
First Equation:
\( t_1 = \frac{2}{1.6} = 1.25 \, \text{s} \)
Second Equation:
\( t_2 = \frac{2}{0.8 \, g} \)
Substituting \(g = 9.8 \, \text{m/s}^2\):
\( t_2 = \frac{2}{0.8 \times 9.8} = 0.255 \, \text{s} \)
Therefore, the results are:
– Tension (\(T\)): \(0.384 \, \text{N}\)
– Acceleration (\(a\)): \(0.16 \, \text{m/s}^2\)
– Time taken for Q to reach its greatest height (\(t_2\)): \(0.255 \, \text{s}\)