Question
A particle of mass 0.4 kg is projected with a speed of 12 \(ms^{-1} \) up a line of greatest slope of a smooth plane inclined at 30Å to the horizontal.
(i) Find the initial kinetic energy of the particle. up a line of greatest slope of a smooth plane inclined at 30Å to the horizontal.
(ii) Use an energy method to find the distance the particle moves up the plane before coming to instantaneous rest.
▶️Answer/Explanation
(i) To find the initial kinetic energy of the particle,
\(KE = \frac{1}{2}mv^2\)
Where:
– \(KE\) is the kinetic energy.
– \(m\) is the mass of the particle, which is \(0.4 \, \text{kg}\).
– \(v\) is the initial speed, which is \(12 \, \text{m/s}\).
\(KE = \frac{1}{2} \times 0.4 \, \text{kg} \times (12 \, \text{m/s})^2 = 28.8 \, \text{J}\)
So, the initial kinetic energy of the particle is \(28.8 \, \text{J}\).
(ii) To find the distance the particle moves up the inclined plane before coming to instantaneous rest, we can use the principle of conservation of energy. As the particle moves up the slope, its initial kinetic energy decreases, and this loss of kinetic energy is converted into gravitational potential energy.
The change in potential energy (\(\Delta PE\)) is calculated as:
\(\Delta PE = mgh\)
Where:
– \(m\) is the mass of the particle, which is \(0.4 \, \text{kg}\).
– \(g\) is the acceleration due to gravity, which is approximately \(9.8 \, \text{m/s}^2\).
– \(h\) is the vertical height the particle reaches before coming to rest.
The work done in lifting the particle to height \(h\) is equal to this change in potential energy.
Now, the change in potential energy is equal to the initial kinetic energy (\(KE\)) that the particle had when it was projected up the slope.Initial kinetic energy \(28.8 \, \text{J}\). Therefore:
\(\Delta PE = KE = 28.8 \, \text{J}\)
\(0.4 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 \cdot h = 28.8 \, \text{J}\)
\(h = \frac{28.8 \, \text{J}}{0.4 \, \text{kg} \cdot 9.8 \, \text{m/s}^2} = 7.2 \, \text{m}\)
So, the height the particle reaches is \(7.2 \, \text{m}\).
\(\sin \theta = \frac{h}{d}\)
In this case, \(\theta = 30^\circ\) (the angle of the incline) and \(h = 7.2 \, \text{m}\). We can solve for \(d\):
\(d = \frac{h}{\sin \theta} = \frac{7.2 \, \text{m}}{\sin(30^\circ)}\)
\(d = \frac{7.2 \, \text{m}}{0.5} = 14.4 \, \text{m}\)
So, the distance the particle moves up the inclined plane before coming to instantaneous rest is approximately \(14.4 \, \text{m}\).
Question
A lorry of mass 14 000 kg moves along a road starting from rest at a point O. It reaches a point A, and then continues to a point B which it reaches with a speed of 24 m s−1. The part OA of the road is straight and horizontal and has length 400 m. The part AB of the road is straight and is inclined downwards at an angle of θ° to the horizontal and has length 300 m.
(i) For the motion from O to B, find the gain in kinetic energy of the lorry and express its loss in potential energy in terms of θ.
The resistance to the motion of the lorry is 4800 N and the work done by the driving force of the lorry from O to B is 5000 kJ.
(ii) Find the value of Θ.
▶️Answer/Explanation
Given:
– Mass of the lorry, \(m = 14000 \, \text{kg}\)
– Speed at point \(A\), \(v_{\text{A}} = 0 \, \text{m/s}\) (starting from rest)
– Speed at point \(B\), \(v_{\text{B}} = 24 \, \text{m/s}\)
– Resistance to motion, \(R = 4800 \, \text{N}\)
– Work done by the driving force, \(W_{\text{drive}} = 5000 \, \text{kJ} = 5000 \times 10^3 \, \text{J}\)
– Length of OA, \(OA = 400 \, \text{m}\)
– Length of AB, \(AB = 300 \, \text{m}\)
(i) First, let’s find the gain in kinetic energy (\(KE\)) of the lorry and the loss in potential energy (\(PE\)) in terms of \(\theta\).
The gain in kinetic energy can be calculated as the difference between the kinetic energy at point B and the kinetic energy at point A:
\(\Delta KE = \frac{1}{2} m v_{\text{B}}^2 – \frac{1}{2} m v_{\text{A}}^2\)
\(\Delta KE = \frac{1}{2} m (v_{\text{B}}^2 – v_{\text{A}}^2)\)
\(\Delta KE = \frac{1}{2} \times 14000 \times (24^2 – 0^2) \, \text{J}\)
\(\Delta KE = 4032 \times 10^3 \, \text{J}\)
The loss in potential energy is due to the change in height from point A to point B. Using the vertical height change (\(h\)) and gravity:
\(PE \text{ loss} = mgh\)
The vertical height change is \(AB \times \sin(\theta)\):
\(h = AB \times \sin(\theta) = 300 \times \sin(\theta)\)
\(PE \text{ loss} = m \cdot g \cdot h = 14000 \times 9.81 \times 300 \times \sin(\theta)\)
So, the expressions for the gain in kinetic energy and the loss in potential energy in terms of \(\theta\) are:
\(KE \text{ gain} = 4032 \times 10^3\)
\(PE \text{ loss} = 42 \times 10^6 \sin(\theta)\)
(ii) Calculating the value of \(\theta\):
The work done by the driving force equals the sum of the kinetic energy gain, potential energy loss, and the work done against resistance:
\(W_{\text{drive}} = \Delta KE + \Delta PE + W_{\text{resistance}}\)
\(5000 \times 10^3 = 4032 \times 10^3 + 42 \times 10^6 \sin(\theta) + W_{\text{resistance}}\)
Given the resistance force \(R\) is \(4800 \, \text{N}\) over a distance of \(700 \, \text{m}\) (\(OA + AB\)):
\(W_{\text{resistance}} = R \times d = 4800 \times 700 = 3360 \times 10^3 \, \text{J}\)
Substituting \(W_{\text{resistance}}\) back into the equation:
\(5000 \times 10^3 = 4032 \times 10^3 + 42 \times 10^6 \sin(\theta) + 3360 \times 10^3\)
\(5000 \times 10^3 = 4032 \times 10^3 + 42 \times 10^6 \sin(\theta) + 3360 \times 10^3\)
\(1640 \times 10^3 = 42 \times 10^6 \sin(\theta)\)
\(\sin(\theta) = \frac{1640 \times 10^3}{42 \times 10^6}\)
\(\sin(\theta) \approx 0.0390476\)
To find \(\theta\):
\(\theta \approx \sin^{-1}(0.0390476) \approx 2.25^\circ\)
Question
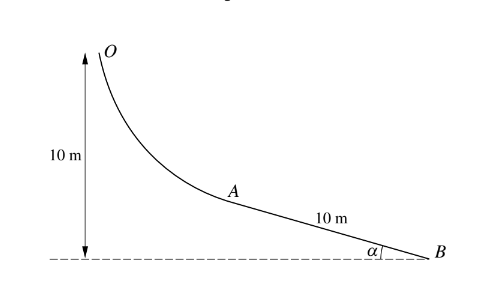
The diagram shows the vertical cross-section OAB of a slide. The straight line AB is tangential to the curve OA at A. The line AB is inclined at α to the horizontal, where sin α = 0.28. The point O is 10 m higher than B, and AB has length 10 m (see diagram). The part of the slide containing the curveOA is smooth and the part containing AB is rough. A particle P of mass 2 kg is released from rest at O and moves down the slide.
(i) Find the speed of P when it passes through A. The coefficient of friction between P and the part of the slide containing AB is \(\frac{1}{12}\). Find
(ii) the acceleration of P when it is moving from A to B,
(iii) the speed of P when it reaches B.
▶️Answer/Explanation
(i) Finding the speed of \(P\) when passing through \(A\):
The potential energy loss can be determined by considering the change in height from \(O\) to \(B\) and the change in potential energy into kinetic energy at \(A\).
Given that the height difference is \(10 \, \text{m}\) and \(\sin \alpha = 0.28\):
\(PE_{\text{loss}} = m \cdot g \cdot (h_{\text{O}} – h_{\text{B}}) = m \cdot g \cdot (10 – 10 \times \sin \alpha)\]
\(PE_{\text{loss}} = 2 \times 9.81 \times (10 – 10 \times 0.28) = 2 \times 9.81 \times 7.2 = 144.144 \, \text{J}\)
The speed at \(A\) is found using the equation for conservation of energy:
\(\text{Initial potential energy at O} = \text{Final kinetic energy at A}\)
\(mgh_{\text{O}} = \frac{1}{2}mv_{\text{A}}^2\)
\(2 \times 9.81 \times 10 = \frac{1}{2} \times 2 \times v_{\text{A}}^2\)
\(v_{\text{A}} = \sqrt{2 \times 9.81 \times 10} = 12 \, \text{m/s}\)
(ii) The acceleration of \(P\) when moving from \(A\) to \(B\):
The net force acting on \(P\) from \(A\) to \(B\) is the difference between the component of the gravitational force parallel to the incline and the frictional force.
The component of the gravitational force acting parallel to the incline:
\(m \cdot g \cdot \sin \alpha = 2 \times 9.81 \times 0.28 = 5.5032 \, \text{N}\)
The frictional force:
\(f = \mu \cdot N = \frac{1}{12} \times m \cdot g = \frac{1}{12} \times 2 \times 19.81 \approx 1.635 \, \text{N}\)
Therefore, the net force acting on the particle:
\(F_{\text{net}} = m \cdot a = m \cdot g \cdot \sin \alpha – f\)
\(2 \cdot a = 5.5032 – 1.635\)
\(a = \frac{3.8682}{2} = 1.9341 \, \text{m/s}^2\)
(iii) The speed of \(P\) when it reaches \(B\):
The final speed of \(P\) at \(B\) can be calculated using the kinematic equation:
\(v_{\text{B}}^2 = v_{\text{A}}^2 + 2as\)
\(v_{\text{B}}^2 = 12^2 + 2 \times 1.9341 \times 10\)
\(v_{\text{B}}^2 = 144 + 38.682 = 182.682\)
\(v_{\text{B}} \approx \sqrt{182.682} \approx 13.51 \, \text{m/s}\)