Question
The total mass of a cyclist and her bicycle is 75 kg. The cyclist ascends a straight hill of length 0.7 km inclined at 1.5Å to the horizontal. Her speed at the bottom of the hill is 10 \(ms^{-1}\) and at the top it is 5\( ms^{-1}\)
. There is a resistance to motion, and the work done against this resistance as the cyclist ascends the hill is 2000 J. The cyclist exerts a constant force of magnitude F N in the direction of motion. Find F.
▶️Answer/Explanation
The work-energy principle states that the net work done on an object is equal to the change in its kinetic energy. We need to find the force exerted by the cyclist (F) to overcome resistance and ascend the hill.
– Initial velocity (v_initial) = 10 m/s
– Final velocity (v_final) = 5 m/s
– Mass (m) = 75 kg
– Distance (d) = 0.7 km = 700 m
– Angle of incline (θ) = 1.5 degrees
– Work done against resistance (W_resistance) = 2000 J
The initial kinetic energy (KE_initial) and final kinetic energy (KE_final) of the cyclist and her bicycle:
\(KE_initial = \frac{1}{2} \times m\times v_initial^2 = \frac{1}{2}\times 75 kg\times 10 m/s^2 = 3750 J\)
\(KE_final = \frac{1}{2}\times m \times \times v_final^2 = \frac{1}{2}\times 75 kg\times (5 m/s)^2 = 937.5 J\)
ΔKE = KE_final – KE_initial = 937.5 J – 3750 J = -2812.5 J
The negative sign indicates a decrease in kinetic energy.
\(W_resistance = 2000 J \)(given)
Net Work \((W_net) = ΔKE + W_resistance\)
\(W_net = -2812.5 J + 2000 J = -812.5 J\)
\(W_cyclist = F \times distance \times cos(θ)\)
\(W_cyclist =F \times 700 m \times cos(1.5^{\circ})\)
\(W_cyclist – W_resistance = W_net\)
\(F \times 700 m \times cos(1.5^{\circ})- 2000 J = -812.5 J\)
\(F \times 700 m \times cos(1.5^{\circ}) = -812.5 J + 2000 J\)
\(F \times 700 m \times cos(1.5^{\circ}) = 1187.5 J\)
\(F =\frac{118.75}{700\times \cos (1.5^{\circ})}\)
F ≈ 18.5 N
So, the force exerted by the cyclist is approximately 18.5 N.
Question
A tractor of mass 3700 kg is travelling along a straight horizontal road at a constant speed of 12 \(m s^{−1}\). The total resistance to motion is 1150 N.
(i) Find the power output of the tractor’s engine. The tractor comes to a hill inclined at 4Å above the horizontal. The power output is increased to 25 kW and the resistance to motion is unchanged.
(ii) Find the deceleration of the tractor at the instant it begins to climb the hill.
(iii) Find the constant speed that the tractor could maintain on the hill when working at this power.
▶️Answer/Explanation
(i) The power output of the tractor’s engine on the horizontal road is correctly calculated as:
\(P = \text{Resistance} \times \text{Velocity} = 1150 \, \text{N} \times 12 \, \text{m/s} = 13,800 \, \text{W}\)
So, the power output on the horizontal road is 13,800 W, which is equivalent to 13.8 kW.
(ii) The deceleration (negative acceleration) is correctly calculated using the work-energy principle:
\(F_{\text{driving}} = \frac{25000 \, \text{W}}{12 \, \text{m/s}}\)
\(a = \frac{F_{\text{driving}} – \text{Resistance} – \text{Weight component parallel to the hill}}{m} = \frac{25000/12 – 1150 – 3700g \sin(4^\circ)}{3700}\)
Calculating this gives \(a \approx -0.445 \, \text{m/s}^2\), indicating deceleration.
(iii) The constant speed on the hill is correctly calculated using the power formula:
\(\frac{25000 \, \text{W}}{v} = 1150 + 3700g \sin(4^\circ)\)
\(v = \frac{25000 \, \text{W}}{1150 + 3700g \sin(4^\circ)} \approx 6.70 \, \text{m/s}\)
So, the constant speed that the tractor can maintain on the hill when working at 25 kW is approximately 6.70 m/s.
Question
A car of mass 800 kg is moving up a hill inclined at 1Å to the horizontal, where sin 1 = 0.15. The initial speed of the car is 8\( m s^{−1}\). Twelve seconds later the car has travelled 120 m up the hill and hasspeed 14\( m s^{−1}\).
(i) Find the change in the kinetic energy and the change in gravitational potential energy of the car.
(ii) The engine of the car is working at a constant rate of 32 kW. Find the total work done against the resistive forces during the twelve seconds.5(ii)
▶️Answer/Explanation
(i) The change in kinetic energy (\(ΔKE\)) and the change in gravitational potential energy (\(ΔPE\))
\(ΔKE = \frac{1}{2} \times 800 \times (14^2 – 8^2) = 52,800 \, \text{J}\)
\(ΔPE = 800 \times 10 \times 120 \times 0.15 = 144,000 \, \text{J}\)
So, \(ΔKE\) is 52,800 J, and \(ΔPE\) is 144,000 J. Your calculations for these values are correct.
(ii) The work done by the engine is correctly calculated as:
\(WD \, \text{by} \, \text{engine} = 32,000 \times 12 = 384,000 \, \text{J}\)
Now, to find the total work done against the resistive forces (\(WD \, \text{against} \, F\)),
\(WD \, \text{by} \, \text{engine} = 144,000 + 52,800 + WD \, \text{against} \, F\)
Now, solving for \(WD \, \text{against} \, F\):
\(WD \, \text{against} \, F = 384,000 – 144,000 – 52,800 = 187,200 \, \text{J}\)
So, the total work done against the resistive forces during the twelve seconds is indeed 187,200 J.
The total mass of a cyclist and her bicycle is 70 kg. The cyclist is riding with constant power of 180W up a straight hill inclined at an angle α to the horizontal, where sin α = 0.05. At an instant when the cyclist’s speed is 6 m s−1 , her acceleration is −0.2m s−2. There is a constant resistance to motion of magnitude F N.
(a) Question
Find the value of F.
▶️Answer/Explanation
Forward force exerted by cyclist driving force = \(\frac{180}{6}=30N \)
DF – F – 70g sin α = 70 × ‒ 0.2
30 – F – 70g × 0.05 = 70 × ‒ 0.2
F = 9
(b) Question
Find the steady speed that the cyclist could maintain up the hill when working at this power.
▶️Answer/Explanation
Ans:
\(\frac{180}{v}\) – F – 70g × sin α = 0
v = 4.09 m s−1
A car of mass mkg is towing a trailer of mass 300 kg down a straight hill inclined at \(3^{\circ} \)to the horizontal at a constant speed. There are resistance forces on the car and on the trailer, and the total work done against the resistance forces in a distance of 50 m is 40 000 J. The engine of the car is doing no work and the tow-bar is light and rigid.
(a) Question
Find the value of m.
The resistance force on the trailer is 200 N.
▶️Answer/Explanation
The potential energy (PE) lost as the car and trailer move downhill is calculated using the following formula:
\(PE = mgh\)
Where:
– \(m\) is the mass of the object (in this case, the car and trailer combined),
– \(g\) is the acceleration due to gravity (approximately \(9.81 \, \text{m/s}^2\)),
– \(h\) is the vertical height descended.
\(PE – \text{Work Done Against Resistance} = 0\)
The work done against resistance forces is \(40,000 \, \text{J}\).
\((m + 300)gh – 40,000 = 0\)
We know that the angle of the hill is \(3^\circ\), and we convert this angle to radians:
\(3^\circ = \frac{\pi}{180} \, \text{radians}\)
The solution shows that the mass of the car (\(m\)) is approximately \(1230 \, \text{kg}\) to three significant figures.
This value of \(m = 1230 \, \text{kg}\) ensures that the total potential energy lost is balanced by the work done against resistance, resulting in a constant speed.
Alternative method
Resistance force R = \(\frac{40000}{50}\left [ =800N \right ]\)
(m + 300)g sin 3 – R = 0
m = 1230 to 3 sf
(b) Question
Find the tension in the tow-bar between the car and the trailer.
▶️Answer/Explanation
The force equations for the car and the trailer should be as follows:
For the trailer:
\(T + 300g\sin(3^\circ) – 200 = 0\)
\(T=200-300\times 10\times \sin 3^{\circ}\)
T=43N
Question
A crane is used to raise a block of mass 600 kg vertically upwards at a constant speed through a height of 15 m. There is a resistance to the motion of the block, which the crane does 10 000 J of work to overcome.
(a) Question
Find the total work done by the crane.
▶️Answer/Explanation
(a) To find the total work done by the crane, we need to consider the work done against gravity and the work done to overcome the resistance to motion. The work done against gravity can be calculated using the formula:
\(W_{\text{gravity}} = mgh\)
Where:
\(m\) = mass of the block = 600 kg
\(g\) = acceleration due to gravity = 9.81 m/s² (approximately)
\(h\) = height through which the block is raised = 15 m
Now, calculate \(W_{\text{gravity}}\):
\(W_{\text{gravity}} = 600 \, \text{kg} \times 9.81 \, \text{m/s}^2 \times 15 \)
\( text{m} = 90,000 \, \text{J}\)
The work done to overcome resistance is given as \(10,000 \, \text{J}\).
To find the total work done by the crane, sum these two values:
\(W_{\text{total}} = W_{\text{gravity}} + W_{\text{resistance}} = 90,000 \, \text{J} + 10,000 \, \text{J} = 1,00,000 \, \text{J}\)
So, the total work done by the crane is \(1,00,000 \, \text{J}\).
(b) Question
Given that the average power exerted by the crane is 12.5 kW, find the total time for which the block is in motion.
▶️Answer/Explanation
(b) The average power exerted by the crane can be calculated using the formula:
\(P = \frac{W}{t}\)
Where:
\(P\) = power (12.5 kW)
\(W\) = work done (1,00,000 J)
\(t\) = time (in seconds)
First, convert the power from kilowatts to watts (1 kW = 1000 W):
\(12.5 \, \text{kW} = 12.5 \times 1000 \, \text{W} = 12,500 \, \text{W}\)
\(t = \frac{W}{P} = \frac{1,00,000 \, \text{J}}{12,500 \, \text{W}}\)
\(t =8 \, \text{s}\)
So, the total time for which the block is in motion is approximately \(8 \, \text{s}\).
Question
A car of mass 1600 kg travels at constant speed 20 ms up a straight road inclined at an angle of sin−1 0.12 to the horizontal.
(a) Question
Find the change in potential energy of the car in 30 s.
▶️Answer/Explanation
The speed of the car is 20 m/s, and it travels for 30 seconds, so the distance it covers (s) is given by:
s = speed × time = 20 m/s × 30 s = 600 meters
The angle of inclination is given by \(\sin^{-1} 0.12\), which is the same as finding the angle whose sine is 0.12. This angle represents the angle between the inclined road and the horizontal.
The change in potential energy (PE) is calculated using the formula for gravitational potential energy:
\[PE = m × g × h\]
Where:
– \(m\) is the mass of the car (1600 kg).
– \(g\) is the acceleration due to gravity (approximately 9.81 m/s²).
– \(h\) is the vertical height through which the car moves.
\(h = s × \sin(\sin^{-1} 0.12)\)
\(h = 600 m × 0.12\)
\(h = 72 m\)
\(PE = 1600 kg × 9.81 m/s² × 72 m\)
\(PE = 1,152,000 J\)
So, the change in potential energy of the car in 30 seconds is 1,152,000 joules. This represents the energy gain due to the car’s ascent along the inclined road.
(b) Question
Given that the total work done by the engine of the car in this time is 1960 kJ, find the constant force resisting the motion.
▶️Answer/Explanation
Total work done by the engine (W) = 1960 kJ = 1960 × 1000 J
Change in potential energy (PE) = 1152000 J (as calculated earlier)
\(WD_{res} = W – \text{PE}\)
\(WD_{res} = 1960 \times 1000 \, \text{J} – 1152000 \, \text{J} = 808000 \, \text{J}\)
\(R=\frac{WD_{res} }{600}\)
\(R=\frac{808000}{600}\)
R=1346.6N
(c) Question
Calculate, in kW, the power developed by the engine of the car.
▶️Answer/Explanation
To calculate the power developed by the engine of the car,
\( \text{Power} = \frac{\text{Work Done}}{\text{Time}} \)
The work done by the engine (W) as 1960 kJ, which is 1960 × 1000 J.
\( \text{Power} = \frac{1960 \times 1000 \, \text{J}}{30 \, \text{s}} \)
1960 kJ to joules: 1960 kJ = 1960 × 1000 J
\( \text{Power} = \frac{1960 \times 1000 \, \text{J}}{30 \, \text{s}} \)
\( \text{Power} \approx 65333.33 \, \text{W} \)
To express this power in kilowatts (kW), divide by 1000:
\( \text{Power} \approx \frac{65333.33 \, \text{W}}{1000} \approx 65.33 \, \text{kW} \)
So, the power developed by the engine of the car is approximately 65.33 kW.
(d) Question
Given that this power is suddenly decreased by 15%, find the instantaneous deceleration of the car.
▶️Answer/Explanation
\(0.85 \times \frac{196000}{3}= DF\times 20\)
\(DF – R – 1600g \times 0.12 = 1600a\)
\(\left [ \frac{8330}{3} – \frac{4040}{3} – 1920 = 1600a \right ]\)
\(a = – 0.306ms^{-2}\)
The deceleration is \(- 0.306ms^{-2}\).
Question
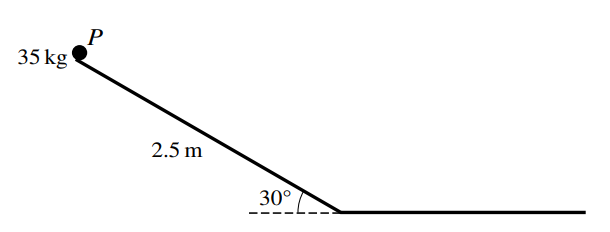
A slide in a playground descends at a constant angle of 30o for 2.5 m. It then has a horizontal section in the same vertical plane as the sloping section. A child of mass 35 kg, modelled as a particle P, starts from rest at the top of the slide and slides straight down the sloping section. She then continues along the horizontal section until she comes to rest (see diagram). There is no instantaneous change in speed when the child goes from the sloping section to the horizontal section.
The child experiences a resistance force on the horizontal section of the slide, and the work done against the resistance force on the horizontal section of the slide is 250 J per metre.
(a) It is given that the sloping section of the slide is smooth.
(i) Find the speed of the child when she reaches the bottom of the sloping section.
(ii) Find the distance that the child travels along the horizontal section of the slide before she
comes to rest.
(b) It is given instead that the sloping section of the slide is rough and that the child comes to rest on
the slide 1.05 m after she reaches the horizontal section.
Find the coefficient of friction between the child and the sloping section of the slide.
▶️Answer/Explanation
(a) (i) PE = 35 × 2.5sin30
\(\frac{1}{2}\times 35v^{2}=35g\times 2.5\sin 30\)
v= 5 m s–1
Alternative method for Question (a)(i)
mg sin30= ma leading to a= 5
v = 0 + 2 × 5 × 2.5
v= 5 m s–1
(a) (ii) \(\frac{1}{2}\times 35\times 5^{2}=250d\)
d =1.75 m
Alternative method for Question (a)(ii)
\(-250=35a\ leading \ to \ a=-\frac{50}{7}=-7.14\)
0 = 52 + 2 (a) (d)
d =1.75 m
(b) \(\frac{1}{2}\times 35v^{2}=250\times 1.05[v^{2}=15]\)
or
\(-250=35a\ leading\ to\ a=-\frac{50}{7}\)
\(O=v^{2}+2\times -\frac{50}{7}\times 1.05 \ [v^{2}=15]\)
R = 35g cos30 [303.11]
v2 = 0 + 2 × a × 2.5 = 15 leading to a = 3
or
PE change = = 35g × 2.5sin 30 [437.5]
35 sin 30 − F = 35a = or [175 − F = 35a]
or
35 × 2.5sin 30 F × 2.5 + \(\frac{1}{2}\times 35\times 15 [437.5=F\times 2.5+262.5]\)
F = μ × R
μ = 0.231
(b) Alternative method for Question (b)
R = 35g cos 30
PE change = = 35g × 2.5sin 30 [437.5 ]
WD against friction on the flat = 250 × 1.5
35g × 2.5sin 30 F × 2.5 + 250 × 1.05 = [437.5 × F 2.5 + 262.5 ]
F = μ × R
μ = 0.231
Question
A car of mass 1400 kg is travelling at constant speed up a straight hill inclined at \(\alpha\) to the horizontal, where \(sin\alpha=0.1\). There is a constant resistance force of magnitude 600 N. The power of the car’s engine is 22500 W.
(a) Show that the speed of the car is \(11.25 ms^{-1}\).
The car, moving with speed \(11.25ms^{-1}\), comes to a section of the hill which is inclined at \(2^o\) to the horizontal.
(b) Given that the power and resistance force do not change, find the initial acceleration of the car up this section of the hill.
▶️Answer/Explanation
(a) – Finding the speed of the car:
The driving force (\(DF\)) is given by the power divided by the velocity:
\( DF = \frac{22500}{v} \)
The equation representing the equilibrium of forces along the incline is:
\( DF – 1400 \cdot g \cdot \sin(\alpha) – 600 = 0 \)
Solving for \(v\):
\( \frac{22500}{v} – 1400 \cdot 9.8 \cdot 0.1 – 600 = 0 \)
\( v = 11.25 \, \text{m/s}^{-1} \)
(b) – Finding the initial acceleration of the car on the new incline
The equation representing the equilibrium of forces along the new incline is:
\( DF – 1400 \cdot g \cdot \sin(2^\circ) – 600 = 1400 \cdot a \)
\( \frac{22500}{11.25} – 1400 \cdot 9.8 \cdot \sin(2^\circ) – 600 = 1400 \cdot a \)
\( a \approx 0.651 \, \text{m/s}^2 \)
Question
A car of mass 1500 kg is pulling a trailer of mass 750 kg up a straight hill of length 800 m inclined at
an angle of sin−1 0.08 to the horizontal. The resistances to the motion of the car and trailer are 400 N
and 200 N respectively. The car and trailer are connected by a light rigid tow-bar. The car and trailer
have speed 30 m s−1 at the bottom of the hill and 20 m s−1 at the top of the hill.
(a) Use an energy method to find the constant driving force as the car and trailer travel up the hill.
After reaching the top of the hill the system consisting of the car and trailer travels along a straight
level road. The driving force of the car’s engine is 2400 N and the resistances to motion are unchanged.
(b) Find the acceleration of the system and the tension in the tow-bar.
▶️Answer/Explanation
(a) KE (final) = ½ × 1500 × 202 + ½ × 750 × 202
KE (initial) = ½ × 1500 × 302 + ½ × 750 × 302
PE gain = 2250 × 10 × 800 × 0.08
WD against friction = 600 × 800
½ × 2250 × 302 + DF × 800 = 600 × 800
+ ½ × 2250 × 202 + 2250 × 10 × 800 × 0.08
DF = 1700 N
(b) 2400 – 600 = 2250a
or
T – 200 = 750a and 2400 – 400 – T = 1500a
Attempting to solve for a or for T
T = 800 N and a = 0.8 ms–2
Question
A car of mass 1400 kg is moving along a straight horizontal road against a resistance of magnitude
350 N.
(a) Find, in kW, the rate at which the engine of the car is working when it is travelling at a constant
speed of 20 m s−1.
(b) Find the acceleration of the car when its speed is 20 m s−1 and the engine is working at 15 kW.
▶️Answer/Explanation
(a)The rate at which the engine is doing work is equal to the power (\(P\)), and power is given by the product of force and velocity:
\( P = F \cdot v, \)
where \( F \) is the force applied by the engine and \( v \) is the velocity of the car.
In this case, the force applied by the engine is the sum of the resistive force (\( F_{\text{res}} \)) and the force required to maintain a constant speed (\( F_{\text{applied}} \)).
The resistive force is given as \( F_{\text{res}} = 350 \, \text{N} \), and the velocity is \( v = 20 \, \text{m/s} \).
Thus, the force applied by the engine is:
\( F_{\text{applied}} = F_{\text{res}} = 350 \, \text{N}. \)
\( P = F_{\text{applied}} \cdot v. \)
\( P = 350 \, \text{N} \times 20 \, \text{m/s} = 7000 \, \text{W} = 7 \, \text{kW}. \)
So, the rate at which the engine is working is \( 7 \, \text{kW} \).
(b)\(15000 = \text{DF} \times 20\) where \(\text{DF} = 750\)
The power equation \(P = \text{DF} \times v\).
\(\text{DF} – 350 = 1400a\)
This equation represents the net force (\(\text{DF} – 350\)) acting on the car, and it is equated to \(1400a\) according to Newton’s second law (\(F = ma\)), where \(a\) is the acceleration.
\(a = \frac{2}{7} \, \text{m/s}^2\)
The acceleration of the car is \(\frac{2}{7} \, \text{m/s}^2\), which is approximately \(0.286 \, \text{m/s}^2\) (since \(\frac{2}{7} \approx 0.286\)).
Question
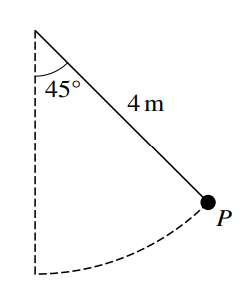
A child of mass 35 kg is swinging on a rope. The child is modelled as a particle P and the rope
is modelled as a light inextensible string of length 4 m. Initially P is held at an angle of 45o to the
vertical (see diagram).
(a) Given that there is no resistance force, find the speed of P when it has travelled half way along
the circular arc from its initial position to its lowest point.
(b) It is given instead that there is a resistance force. The work done against the resistance force
as P travels from its initial position to its lowest point is X J. The speed of P at its lowest point
is 4 m s−1.
Find X.
▶️Answer/Explanation
(a) Attempt at finding PE lost
PE lost = 35 g (4cos22.5 – 4cos45)
\(\frac{1}{2}\times 35v^{2}=35g(4\cos 22.5-4\cos 45)\)
Speed = 4.16 ms–1 (4.1643…)
(b) Use of the work-energy equation in the form: PE lost = KE gain + WD against resistance
\(\frac{1}{2}\times 35\times 4^{2}=35g(4-4\cos 45)=X\)
X = 130 (130.05…)
Question
A car of mass 1800 kg is towing a trailer of mass 400 kg along a straight horizontal road. The car and
trailer are connected by a light rigid tow-bar. The car is accelerating at 1.5 m s−2. There are constant
resistance forces of 250 N on the car and 100 N on the trailer.
(a) Find the tension in the tow-bar.
(b) Find the power of the engine of the car at the instant when the speed is 20 m s−1.
▶️Answer/Explanation
(a)For the car:
\( F_{\text{car, net}} = m_{\text{car}} \cdot a_{\text{car}} + F_{\text{res, car}} \)
\( F_{\text{car, net}} = 1800 \, \text{kg} \times 1.5 \, \text{m/s}^2 + 250 \, \text{N} = 2775 \, \text{N} \)
For the trailer:
\( F_{\text{trailer, net}} = m_{\text{trailer}} \cdot a_{\text{trailer}} + F_{\text{res, trailer}} \)
\( F_{\text{trailer, net}} = 400 \, \text{kg} \times 1.5 \, \text{m/s}^2 + 100 \, \text{N} = 700 \, \text{N} \)
Since the tension in the tow-bar (\(T\)) is equal to the net force on the trailer, you correctly found:
\( T = F_{\text{trailer, net}} = 700 \, \text{N} \)
(b)\( F – 250 – 100 = 2200 \times 1.5 \)
F-350=3300
F=3300+350
F=3650
\( P = F \cdot v \),
where \( F \) is the net force on the system and \( v \) is the velocity.
\(P=3650\times 20\)
P=73000 W
OR
P=73KW
Question

The diagram shows the vertical cross-section of a surface. A, B and C are three points on the cross-section. The level of B is h m above the level of A. The level of C is 0.5m below the level of A. A particle of mass 0.2 kg is projected up the slope from A with initial speed \(5ms^{-1}\). The particle remains in contact with the surface as it travels form A to C.
(a) Given that the particle reaches B with a speed of \(3ms^{-1}\) and that there is no resistance force.
find h.
(b) It is given instead that there is a resistance force and that the particle does 3.1J of work against the resistance force as it travels from A to C.
▶️Answer/Explanation
(a)Initial kinetic energy (\(KE_i\)): \(\frac{1}{2} \times 0.2 \times 5^2\)
Final kinetic energy (\(KE_f\)): \(\frac{1}{2} \times 0.2 \times 3^2\)
Change in Potential Energy:
The change in potential energy is due to the change in height (\(h\)).
Conservation of energy equation: \(KE_i = KE_f + mgh\)
Substitute the expressions for \(KE_i\) and \(KE_f\):
\( \frac{1}{2} \times 0.2 \times 5^2 = 0.2gh + \frac{1}{2} \times 0.2 \times 3^2 \)
\( h = \frac{\frac{1}{2} \times 0.2 \times 5^2 – \frac{1}{2} \times 0.2 \times 3^2}{0.2g} \)
\( h = \frac{0.5 \times 5^2 – 0.5 \times 3^2}{g} \)
\( h = \frac{12.5 – 4.5}{g} = \frac{8}{g} = 0.8 \, \text{m} \)
(b)Work-Energy Equation:
Work done against resistance (\(W_{\text{res}}\)) is given as 3.1 J.
Apply the work-energy equation: \(KE_i – KE_f + \text{Work} = 0.5mv^2\)
Substitute known values:
\( \frac{1}{2} \times 0.2 \times 5^2 – 3.1 + 0.2gh = \frac{1}{2} \times 0.2 \times v^2 \)
\( \frac{1}{2} \times 0.2 \times 5^2 – 3.1 + 0.2gh = \frac{1}{2} \times 0.2 \times v^2 \)
\( \frac{25}{2} – 3.1 + 0.2 \times g \times 0.5 = 0.1v^2 \)
\( 12.5 – 3.1 + 0.1 \times 9.8 \times 0.5 = 0.1v^2 \)
\( 0.2 = 0.1v^2 \)
\( v^2 = 2 \)
\( v = \sqrt{2} = 2 \, \text{m/s} \)
Question
A lorry mass 16 000 kg is travelling along a straight horizontal road. The engine of the lorry is working at constant power. The work done by the driving force in 10s is 750 000 J.
(a) Find the power of the lorry’s engine.
(b) There is a constant resistance force acting on the lorry of magnitude 2400 N.
Find the acceleration of the lorry at an instant when its speed is 25ms^{-1}.
▶️Answer/Explanation
(a)\( P = \frac{W}{\Delta t} = \frac{750000 \, \text{J}}{10 \, \text{s}} = 75000 \, \text{W} \)
or in kilowatts:
\( 75000 \, \text{W} = 75 \, \text{kW} \)
(b)The driving force (\(DF\)) is related to power and velocity (\(v\)):
\( DF = \frac{P}{v} = \frac{75000 \, \text{W}}{25 \, \text{m/s}} \)
The net force (\(F_{\text{net}}\)) is the driving force minus the resistance force:
\( F_{\text{net}} = DF – F_{\text{resistance}} = \frac{75000 \, \text{W}}{25 \, \text{m/s}} – 2400 \, \text{N} \)
Use Newton’s second law \(F_{\text{net}} = ma\) to find acceleration:
\( DF – 2400 = 16000 \, \text{kg} \cdot a \)
\( a = \frac{DF – 2400}{16000} = \frac{75000 \, \text{W}/25 – 2400}{16000} = 0.0375 \, \text{m/s}^2 \)
Question
A lorry has mass 12 000 kg.
(i) The lorry moves at a constant speed of \(5m^{-1}\) up a hill inclined at an angle of 1 to the horizontal,
where sin 1 = 0.08. At this speed, the magnitude of the resistance to motion on the lorry is 1500 N. Show that the power of the lorry’s engine is 55.5 kW. When the speed of the lorry is \(ms^{-1}\) the magnitude of the resistance to motion is \(kv^{2}\) where k is aconstant.
(ii) Show that k = 60.
(iii) The lorry now moves at a constant speed on a straight level road. Given that its engine is still
working at 55.5 kW, find the lorry’s speed.
▶️Answer/Explanation
(i)Driving Force (\(DF\)):
The component of the weight parallel to the incline is \(mg \sin(\theta)\), where \(m\) is the mass, \(g\) is the acceleration due to gravity, and \(\theta\) is the angle of the incline.
\(DF = 12000 \times 9.8 \times 0.08 = 11100 \, \text{N}\)
Power is given by the formula \(P = \text{Force} \times \text{Velocity}\).
\(P = DF \times \text{Velocity} = 11100 \times 5 = 55,500 \, \text{W}\) or \(55.5 \, \text{kW}\).
(ii) \(kv^2 = 1500\) at \(v = 5
\(k(5)^{2}=1500\)
\(k=\frac{1500}{25}\)
k=60
(iii) The air resistance is given by \(DF = kv^2\), where \(k\) is the constant.
\(DF = 60 \times 5^2 = 1500 \, \text{N}\)
On a straight level road, the power (\(P\)) is given by \(P = DF \times \text{Velocity}\).
\(55,500 = 1500 \times \nu^2 \times \nu = 60 \nu^3\).
Solving for \(\nu\): \(\nu = \sqrt[3]{\frac{55,500}{60}} \approx 9.74 \, \text{m/s}\).
Question
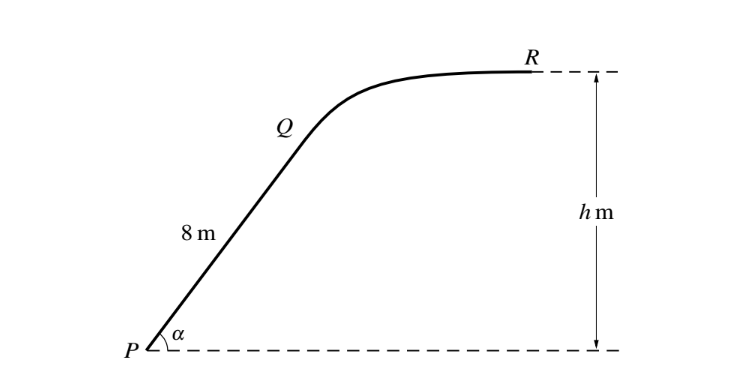
The diagram shows the vertical cross-section PQR of a slide. The part PQ is a straight line of length 8 m inclined at angle ! to the horizontal, where sin ! = 0.8. The straight part PQ is tangential to the curved part QR, and R is h m above the level of P. The straight part PQ of the slide is rough and the curved part QR is smooth. A particle of mass 0.25 kg is projected with speed 15 m \(s^{-1}\) from P towards Q and comes to rest at R. The coefficient of friction between the particle and PQ is 0.5.
(i) Find the work done by the friction force during the motion of the particle from P to Q.
(ii) Hence find the speed of the particle at Q.
(iii )Find the value of h.
▶️Answer/Explanation
(i) Work done against friction:
\( R = 0.25 \ \mathrm{g} \times 0.6 = 1.5 \ \mathrm{J} \)
The force \( F \) is given by:
\( F = 0.5 \times 0.25 \ \mathrm{g} \times 0.6 = 0.75 \ \mathrm{N} \)
The work done against friction (\( W_d \)) is given by:
\( W_d = F \times 8 = 0.75 \ \mathrm{N} \times 8 \ \mathrm{m} = 6 \ \mathrm{J} \)
(ii) Find the final speed \( v \):
\( \frac{1}{2} \times 0.25 \times 15^2 = \frac{1}{2} \times 0.25 \times v^{-2} + 6 + 0.25 \ \mathrm{g} \times 8 \times 0.8 \)
Solving for \( v \):
\( v = 7 \ \mathrm{m/s} \)
Acceleration (\( a \)) is given by:
\( -F – 0.25 \ \mathrm{g} \sin \alpha = 0.25 \ a \)
Solving for \( a \):
\( a = -11 \ \mathrm{m/s^2} \)
(iii) Find the total height \( H \):
\( \frac{1}{2} \times 0.25 \times 7^2 = 0.25 \ \mathrm{g} \times H \)
Solving for \( H \):
\( H = \frac{7^2}{2 \times 9.8} = 2.45 \ \mathrm{m} \)
The total height \( h \) is given by:
\( h = 6.4 + H = 8.85 \ \mathrm{m} \)
Alternatively, using the work-energy principle:
\( \frac{1}{2} \times 0.25 \times 15^2 = 6 + 0.25 \ \mathrm{g} \times h \)
Solving for \( h \):
\( h = 8.85 \ \mathrm{m} \)
Question
A car of mass 1500 kg is pulling a trailer of mass 300 kg along a straight horizontal road at a constant
speed of 20 m\( s^{-1}\). The system of the car and trailer is modelled as two particles, connected by a light rigid horizontal rod. The power of the car’s engine is 6000 W. There are constant resistances to motion of R N on the car and 80 N on the trailer.
(i) Find the value of R.
The power of the car’s engine is increased to 12 500 W. The resistance forces do not change.
(ii) Find the acceleration of the car and trailer and the tension in the rod at an instant when the speed of the car is 25 \(ms^{-1}\)
▶️Answer/Explanation
(i) \( \text{Driving force} = \frac{6000}{20} = 300 \, \mathrm{N} \)
\( R = 300 – 80 = 220 \, \mathrm{N} \)
(ii) Find the acceleration of the car and trailer and the tension in the rod at an instant when the speed of the car is \(25 \, \mathrm{m/s}\):
\( \text{New driving force (DF)} = \frac{12500}{25} = 500 \, \mathrm{N} \)
For the car:
\( DF – T – R = 1500 \)
For the trailer:
\( T – 80 = 300 \)
For the system (car + trailer):
\( DF – 80 – R = 1800 \, \mathrm{N} \, a \)
Solving these equations,
\( a = 0.111 \, \mathrm{m/s^2} \)
\( T = 113 \, \mathrm{N} \)
Question
A van of mass 2500 kg descends a hill of length 0.4 km inclined at 4Å to the horizontal. There is a
constant resistance to motion of 600 N and the speed of the van increases from \( 20ms^{-1}\)to \(30 ms^{-1}\)as it descends the hill. Find the work done by the van’s engine as it descends the hill.
▶️Answer/Explanation
\( KE_{\text{gain}} = \frac{1}{2} \times 2500 \times (30^2 – 20^2) = 625,000 \ \mathrm{J} \)
\( PE_{\text{lost}} = mgh \sin \theta \)
Given
– \( m = 2500 \ \mathrm{kg} \),
– \( g = 9.8 \ \mathrm{m/s^2} \),
– \( h = 400 \ \mathrm{m} \),
– \(\theta = 4^\circ\),
\( PE_{\text{lost}} = 2500 \times 9.8 \times 400 \times \sin(4^\circ) \)
\( PE_{\text{lost}} \approx 2500 \times 9.8 \times 400 \times 0.06976 \)
\( PE_{\text{lost}} \approx 697,564.7 \ \mathrm{J} \)
Now, the total work done is the sum of the work done by the engine and the potential energy lost:
\( \text{Work done} = \text{Work done by engine} + \text{PE lost} \)
\( \text{Work done} = 600 \times 400 + 625,000 + 697,564.7 \)
Now, calculate the total work done:
\( \text{Work done} \approx 167,435.2 \ \mathrm{J} \)
So, the value for the work done by the van’s engine as it descends the hill is approximately \(167,435.2 \ \mathrm{J}\).
Question
A high-speed train of mass 490 000 kg is moving along a straight horizontal track at a constant speed of\( 85 ms^{-1}\). The engines are supplying 4080 kW of power.
(i) Show that the resistance force is 48 000 N.
(ii) The train comes to a hill inclined at an angle \(\Theta \) above the horizontal, where \(sin \Theta =\frac{1}{200}\) . Given that the resistance force iunchanged, find the power required for the train to keep moving at the same constant speed of\( 85 ms^{-1}\).
▶️Answer/Explanation
(i) Show that the resistance force is \(48000 \ \mathrm{N}\):
The power (\(P\)) is given by the equation \(P = Fv\), where \(F\) is the force and \(v\) is the speed.
Given that the power is \(4080 \ \mathrm{kW} = 4080 \times 10^3 \ \mathrm{W}\) and the speed is \(85 \ \mathrm{m/s}\), we can rearrange the formula to find the force (\(F\)):
\( F = \frac{P}{v} \)
\( F = \frac{4080 \times 10^3}{85} \)
\( F \approx 48000 \ \mathrm{N} \)
So, the resistance force is indeed \(48000 \ \mathrm{N}\).
(ii)\(
\begin{aligned}
& \text{(ii) } DF = \frac{P}{v} \\
& DF – 48000 – 490000 \times g \times \frac{1}{200} = 0 \\
& P = DF \times v = 72500 \times 85 = 6.16 \ \mathrm{MW}
\end{aligned}
\)
So, the power required for the train to keep moving at the same constant speed of \(85 \ \mathrm{m/s}\) on the inclined hill is approximately \(6.16 \ \mathrm{MW}\).
Question
A car of mass 1200 kg has a greatest possible constant speed of 60 m s^{−1} along a straight level road. When the car is travelling at a speed of v \(m s^{−1}\) there is a resistive force of magnitude 35v N.
(i) Find the greatest possible power of the car.
(ii) The car travels along a straight level road. Show that, at an instant when its speed is 30\( m s^{−1}\),the greatest possible acceleration of the car is \(2.625 m s^{−2}\).
(iii) The car travels at a constant speed up a hill inclined at an angle of \(sin^{-1}\frac{7}{48}\) to the horizontal.
Find the greatest possible speed of the car.
▶️Answer/Explanation
(i) Find the greatest possible power of the car:
The power (\(P\)) is given by the formula \(P = Fv\), where \(F\) is the force and \(v\) is the speed.
Given that the resistive force (\(F\)) is \(35v\), the power is:
\( P = Fv = (35v)v = 35v^2 \)
Now, we know that the car has the greatest possible constant speed of \(60 \ \mathrm{m/s}\). Substitute this value:
\( P = 35 \times (60)^2 \)
Calculate \(P\):
\( P = 126000 \ \mathrm{W} \)
So, the greatest possible power of the car is \(126000 \ \mathrm{W}\) or \(126 \ \mathrm{kW}\).
(iii) The greatest possible speed of the car up a hill inclined at an angle of \(\sin^{-1}\frac{7}{48}\) to the horizontal:
We are given that the resistive force (\(F_{\text{resistive}}\)) acting against the car’s motion on the hill is \(35v\). The component of the weight of the car along the incline (\(F_{\text{gravity}}\)) is \(mg\sin(\theta)\), where \(\theta\) is the angle of the incline.
The net force (\(F_{\text{net}}\)) acting on the car is given by:
\( F_{\text{net}} = F_{\text{gravity}} – F_{\text{resistive}} \)
For the car to move at a constant speed up the hill, the net force must be equal to \(ma\), where \(a\) is the acceleration and \(m\) is the mass of the car.
\( ma = F_{\text{gravity}} – F_{\text{resistive}} \)
\( ma = mg\sin(\theta) – 35v \)
Given that \(m = 1200 \ \mathrm{kg}\), \(g = 9.8 \ \mathrm{m/s^2}\), and \(\sin^{-1}\frac{7}{48}\) is the angle \(\theta\), substitute these values:
\( ma = 1200 \times 9.8 \times \frac{7}{48} – 35v \)
\( ma = \frac{1200 \times 9.8 \times 7}{48} – 35v \)
\( 35v^2 + 1750v – 126000 = 0 \)
This is a quadratic equation in the form \(av^2 + bv + c = 0\), where \(a = 35\), \(b = 1750\), and \(c = -126000\). You can solve it using the quadratic formula:
\( v = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \)
\( v = \frac{-1750 \pm \sqrt{1750^2 – 4 \times 35 \times (-126000)}}{2 \times 35} \)
\( v = \frac{-1750 \pm \sqrt{3062500 + 17640000}}{70} \)
\( v = \frac{-1750 \pm \sqrt{20602500}}{70} \)
\( v = \frac{-1750 \pm 2860.443}{70} \)
There are two possible solutions:
\( v_1 = \frac{-1750 + 2860.443}{70} \approx 40 \ \mathrm{m/s} \) (positive solution)
\( v_2 = \frac{-1750 – 2860.443}{70} \approx -22 \ \mathrm{m/s} \) (discard since speed cannot be negative in this context)
So, the valid solution is \( v = 40 \ \mathrm{m/s} \). Therefore, the greatest possible speed of the car up the hill inclined at an angle of \(\sin^{-1}\frac{7}{48}\) to the horizontal is \(40 \ \mathrm{m/s}\).
Question
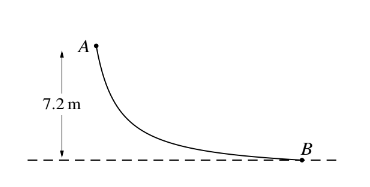
A girl, of mass 40 kg, slides down a slide in a water park. The girl starts at the point A and slides to the point B which is 7.2 metres vertically below the level of A, as shown in the diagram.
(i) Given that the slide is smooth and that the girl starts from rest at A, find the speed of the girl at B.
(ii) It is given instead that the slide is rough. On one occasion the girl starts from rest at A and reaches B with a speed of 10 \(m s^{−1}\). On another occasion the girl is pushed from A with an initial speed V \(m s^{−1}\) and reaches B with speed 11 \(m s^{−1}\). Given that the work done against friction is the same on both occasions, find V.
▶️Answer/Explanation
(i) Smooth Slide:
Given \(h = 7.2 \ \mathrm{m}\) and \(g = 9.8 \ \mathrm{m/s^2}\), we can find the speed (\(v\)) of the girl at point B using the conservation of energy:
\( v = \sqrt{2gh} \)
\( v = \sqrt{2 \times 9.8 \times 7.2} \)
\( v \approx \sqrt{141.12} \approx 11.89 \ \mathrm{m/s} \)
So, the speed of the girl at point B is approximately \(11.89 \ \mathrm{m/s}\).
(ii) Rough Slide:
The work done against friction is the same on both occasions, and it is equal to the change in kinetic energy. We can set up an equation using the principle of conservation of energy:
\( \frac{1}{2}m(v_f^2 – v_i^2) = \frac{1}{2}m(10^2 – 0^2) \)
For the second occasion when the girl is pushed from A with an initial speed \(V\) and reaches B with speed \(11 \ \mathrm{m/s}\):
\( \frac{1}{2}m(11^2 – V^2) = \frac{1}{2}m(10^2 – 0^2) \)
\( \frac{1}{2} \times 40 \times (121 – V^2) = \frac{1}{2} \times 40 \times 100 \)
\( 121 – V^2 = 100 \)
\( V^2 = 21 \)
\( V = \sqrt{21} \)
So, the initial speed \(V\) is \(\sqrt{21} \ \mathrm{m/s}\).
Question
A car of mass 900 kg is moving on a straight horizontal road ABCD. There is a constant resistance of magnitude 800 N in the sections AB and BC, and a constant resistance of magnitude R N in the
section CD. The power of the car’s engine is a constant 36 kW.
(i) The car moves from A to B at a constant speed in 120 s. Find the speed of the car and the distance AB.
The car’s engine is switched off at B.
(ii) The distance BC is 450 m. Find the speed of the car at C.
(iii) The car comes to rest at D. The distance AD is 6637.5 m. Find the deceleration of the car and the value of R.
▶️Answer/Explanation
(i) Given that the car moves from A to B at a constant speed in 120 seconds, and the power of the engine is \(36 \, \text{kW}\), we can use the formula \(P = Fv\) to find the force applied by the engine. Here, \(P\) is the power, \(F\) is the force, and \(v\) is the velocity.
\( F \times v = Pt \)
\( F \times v = 36 \times 10^3 \times 120 \)
\( F \times v = 4.32 \times 10^5 \)
Since the resistance during this period is \(800 \, \text{N}\), we can find the velocity (\(v\)) using \(F \times v = 4.32 \times 10^5\).
\( 800 \times v = 4.32 \times 10^5 \)
\( v = \frac{4.32 \times 10^5}{800} = 540 \, \text{m/s} \)
Now, use the velocity and time to find the distance (\(AB = vt\)).
\( AB = 540 \times 120 = 5400 \, \text{m} \)
(ii) Speed at C:
Since the engine is switched off at B, the car moves due to inertia and resistance forces. The net force is given by \(F_{\text{net}} = F_{\text{resistance}} – F_{\text{engine}}\). The acceleration \(a\) is found using Newton’s second law (\(a = \frac{F_{\text{net}}}{m}\)).
\( a = \frac{F_{\text{resistance}} – F_{\text{engine}}}{m} \)
Substitute the known values:
\( a = \frac{-800 – (-36000/450)}{900} = -\frac{8}{9} \, \text{m/s}^2 \)
Now, use the kinematic equation \(v^2 = u^2 + 2as\) to find the final velocity (\(v\)) at C, where \(u\) is the initial velocity (the velocity at B) and \(s\) is the distance BC.
\( v^2 = 35^2 + 2 \times \left(-\frac{8}{9}\right) \times 450 \)
\( v^2 = 35^2 – 800 \)
\( v = \sqrt{35^2 – 800} = 35 \, \text{m/s} \)
(iii) Since the car comes to rest at D, the final velocity \(v\) is zero. Use the kinematic equation \(v^2 = u^2 + 2as\) to find the deceleration \(a\) during the distance AD.
\( 0^2 = 35^2 + 2a \times 787.5 \)
\( a = -\frac{35^2}{2 \times 787.5} = -0.77 \, \text{m/s}^2 \)
Now, find the resistive force \(R\) using \(R = ma\):
\( R = 900 \times (-0.77) = -700 \, \text{N} \)
Question
A constant resistance of magnitude 1350 N acts on a car of mass 1200 kg.
(i) The car is moving along a straight level road at a constant speed of 32 m s−1. Find, in kW, the rate at which the engine of the car is working.
(ii) The car travels at a constant speed up a hill inclined at an angle of ∅ to the horizontal, where sin ∅ = 0.1, with the engine working at 76.5 kW. Find this speed.
▶️Answer/Explanation
(i) Constant speed on a straight level road:
\( F_{\text{net}} = -1350 \, \text{N} \)
\( P = F_{\text{net}} \cdot v = -1350 \cdot 32 \)
\( P = -43200 \, \text{W} = -43.2 \, \text{kW} \)
The negative sign indicates that the power is being provided by the car’s engine to overcome the resistance.
(ii) Constant speed up a hill:
\( F_{\text{net}} = 1350 + 1200 \cdot 9.8 \cdot \sin(\varphi) \)
\( F_{\text{net}} = 1350 + 1200 \cdot 9.8 \cdot 0.1 \)
\( F_{\text{net}} = 1350 + 1176 \)
\( F_{\text{net}} = 2526 \, \text{N} \)
Now, using \(P = F_{\text{net}} \cdot v\):
\( 76.5 \times 10^3 = 2526 \cdot v \)
\( v \approx \frac{76.5 \times 10^3}{2526} \)
\( v \approx 30.29 \, \text{m/s} \)
Therefore, the car’s speed up the hill is approximately \(30.29 \, \text{m/s}\) when the engine is working at \(76.5 \, \text{kW}\).
Question
A lorry of mass 24 000 kg is travelling up a hill which is inclined at 3° to the horizontal. The power developed by the lorry’s engine is constant, and there is a constant resistance to motion of 3200 N.
(i) When the speed of the lorry is 25 m s−1, its acceleration is 0.2 m s−2. Find the power developed by the lorry’s engine.
(ii) Find the steady speed at which the lorry moves up the hill if the power is 500 kW and the resistance remains 3200 N.
▶️Answer/Explanation
(i) Power when the speed is \(25 \, \text{m/s}\) and acceleration is \(0.2 \, \text{m/s}^2\):
\( F – 24000g \sin 3 – 3200 = 24000 \times (0.2) \)
\( F = 24000g \sin 3 + 3200 + 24000 \times (0.2) \)
Now,
\( \text{Power} = F \times v = 20561 \times 25 \)
\(\text{Power} = 514 \, \text{kW} \)
(ii) Steady speed with constant power of \(500 \, \text{kW}\):
\( \text{Net Force} = 3200 + 24000g \sin 3 \)
\( \text{Net Force} = 3200 + 12560.6295 \)
\( \text{Net Force} = 15760.6295 \, \text{N} \)
\( v = \frac{500000}{15760.6295} \approx 31.7 \, \text{m/s} \)
Question
A weightlifter performs an exercise in which he raises a mass of 200 kg from rest vertically through a distance of 0.7 m and holds it at that height.
(i) Find the work done by the weightlifter.
(ii) Given that the time taken to raise the mass is 1.2 s, find the average power developed by the weightlifter.
▶️Answer/Explanation
(i) The work done by the weightlifter is given by the change in potential energy:
\(W = \Delta PE = m \cdot g \cdot h\)
Where:
– \(W\) is the work done (in joules),
– \(m\) is the mass (in kilograms),
– \(g\) is the acceleration due to gravity (approximately 9.81 m/s²), and
– \(h\) is the height (in meters).
\(W = 200 \, \text{kg} \times 10 \, \text{m/s²} \times 0.7 \, \text{m} = 1400 \, \text{Joules}\)
So, the work done by the weightlifter is 1400 J.
(ii) The average power developed by the weightlifter is given by:
\(P = \frac{W}{t}\)
Where:
– \(P\) is the power (in watts),
– \(W\) is the work done (in joules), and
– \(t\) is the time taken (in seconds).
\(P = \frac{1400 \, \text{J}}{1.2 \, \text{s}} = 1170 \, \text{W}\)
So, the average power developed by the weightlifter is 1170 watts.
Question
A cyclist and her bicycle have a total mass of 84 kg. She works at a constant rate of P W while moving on a straight road which is inclined to the horizontal at an angle θ, where sin θ = 0.1. When moving uphill, the cyclist’s acceleration is 1.25 m s−2 at an instant when her speed is 3 m s−1. When moving downhill, the cyclist’s acceleration is 1.25 m s−2 at an instant when her speed is 10 m s−1. The resistance to the cyclist’s motion, whether the cyclist is moving uphill or downhill, is R N. Find the values of P and R.
▶️Answer/Explanation
When the cyclist is moving uphill:
– The net force required to move uphill at the given acceleration is given by \(F_{\text{up}} = m \cdot a + R\).
– Using Newton’s second law, we can calculate the driving force:
\(F_{\text{up}} = \frac{P}{v} = \frac{P}{3}\) (where \(v\) is the speed of 3 m/s).
– The component of gravity acting along the incline is \(m \cdot g \cdot \sin \theta = 84 \cdot 9.81 \cdot 0.1\).
When the cyclist is moving downhill:
– The net force required to move downhill at the given acceleration is given by \(F_{\text{down}} = R – m \cdot a\).
– Using Newton’s second law, we can calculate the driving force:
\(F_{\text{down}} = \frac{P}{v} = \frac{P}{10}\) (where \(v\) is the speed of 10 m/s).
Now, we have two equations:
– For uphill: \(R + 84 \cdot 9.81 \cdot 0.1 + 84 \cdot 1.25 = \frac{P}{3}\)
– For downhill: \(R – 84 \cdot 1.25 = \frac{P}{10}\)
\(P\left ( \frac{1}{3}-\frac{1}{10} \right )-168=0\)
P=720 W
Now putting value of P in euqation 1
\(R=\frac{720}{3}-84-105\)
R = 51 N
Question
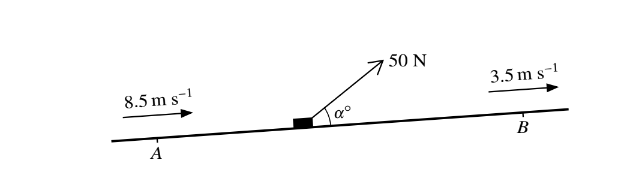
A block of mass 60 kg is pulled up a hill in the line of greatest slope by a force of magnitude 50 N acting at an angle !Å above the hill. The block passes through points A and B with speeds 8.5\( ms^{-1}\) and \(3.5 ms^{-2}\) respectively (see diagram). The distance AB is 250 m and B is 17.5 m above the level of A. The resistance to motion of the block is 6 N. Find the value of \(\alpha \)
▶️Answer/Explanation
PE change = 60 g × 17.5 or
KE change = 1⁄2 60(8.52– 3.52)
[PE = 10500]
KE change = 1⁄2 60(8.52– 3.52) or
PE change = 60 g × 17.5
[KE = 1800]
WD against resistance = 6 × 250 [= 1500]
WD by pulling force =50 cosα × 250
WD = 10500 – 1800 + 1500
10200 J or 10.2 kJ
For using WD = Fdcosα
10200 = 50 × 250 cosα
α = 35.3
Question
A car of mass 800 kg is moving on a straight horizontal road with its engine working at a rate of
22.5 kW. Find the resistance to the car’s motion at an instant when the car’s speed is \(18 ms^{-1}\) and its acceleration is\( 1.2 ms^{-2}\)
▶️Answer/Explanation
To find the resistance to the car’s motion, you can use the following equation that relates power, force, and velocity:
\(P = F \cdot v\)
Where:
– \(P\) is power (in watts, W)
– \(F\) is force (in newtons, N)
– \(v\) is velocity (in meters per second, \(m/s\))
In this case, you are given the power (\(P\)) of the engine as \(22.5 \, kW\),
\(P = 22.5 \, kW = 22,500 \, W\)
Now, since the car’s engine is working against resistance, the power output by the engine should overcome the resistance, and you can use the following equation:
\(P = F \cdot v\)
\(F = \frac{P}{v}\)
Substitute the given values:
\(F = \frac{22,500 \, W}{18 \, m/s} = 1250 \, N\)
Now ,for resistance
\(F – R = 800 \times 1.2 \)
\(1250-R=800\times 1.2\)
R=290N
So, the resistance to the car’s motion at that instant is 290 N
.
Question

A car of mass 1100 kg starts from rest at O and travels along a road OAB. The section OA is straight, of length 1760 m, and inclined to the horizontal with A at a height of 160 m above the level of O. The section AB is straight and horizontal (see diagram). While the car is moving the driving force of the car is 1800 N and the resistance to the car’s motion is 700 N. The speed of the car is \(v m s^{-1}\)when the car has travelled a distance of x m from O.
(i) For the car’s motion from O to A, write down its increase in kinetic energy in terms of v and its increase in potential energy in terms of x. Hence find the value of k for which \(kv^{2}\) = x for 0 ≤ x ≤ 1760.
(ii) Show that\( v^{2}\)= 2x − 3200 for x ≥ 1760.
▶️Answer/Explanation
(i) KE gain = \(550v^{2}\)
PE gain = 1000x
\([1800x=550v^{2}+1000x+700x]\)
(ii) At A \(5.5v^{2}=1760\rightarrow v^{2}=320\)
\(550(v^{2}-320)\)=1800(x-1760)-700(x-1760)
\(v^{2}=2x-3200 \)(cw0)
Alternative for part (ii)
[1800 – 700 = 1100a and \(5.5v^{2}=1760]\)
a = 1 and\( v^{2}=320
[v^{2}=320+2\times 1\times (x-1760)]
v^{2}=2x-3200\)
Question
A train is moving at constant speed\( V ms^{-1}\) along a horizontal straight track. Given that the power of the train’s engine is 1330 kW and the total resistance to the train’s motion is 28 kN, find the value of V.
▶️Answer/Explanation
To find the speed (\(V\)) of the train, we can use the formula for power:
\(\text{Power} = \text{Force} \times \text{Velocity}\)
The total resistance to the train’s motion is given as 28 kN (kilonewtons), which is equivalent to 28,000 N (since 1 kN = 1000 N). So, the force due to resistance (\(F\)) is 28,000 N.
The power of the train’s engine is 1330 kW, which is equivalent to 1,330,000 W (since 1 kW = 1000 W).
Now, we can rearrange the power formula to solve for velocity (\(V\)):
\(\text{Power} = \text{Force} \times \text{Velocity}\)
\(1,330,000 \, \text{W} = 28,000 \, \text{N} \times V\)
\(V = \frac{1,330,000 \, \text{W}}{28,000 \, \text{N}}\)
\(V = 47.5 \, \text{m/s}\)
So, the speed of the train is \(47.5 \, \text{m/s}\).
Question
A lorry of mass 15 000 kg climbs from the bottom to the top of a straight hill, of length 1440 m, at a constant speed of 15 m s−1. The top of the hill is 16 m above the level of the bottom of the hill. The resistance to motion is constant and equal to 1800 N.
(i) Find the work done by the driving force.
On reaching the top of the hill the lorry continues on a straight horizontal road and passes through a point P with speed 24 m s−1. The resistance to motion is constant and is now equal to 1600 N. The work done by the lorry’s engine from the top of the hill to the point P is 5030 kJ.
(ii) Find the distance from the top of the hill to the point P.
▶️Answer/Explanation
(i)
– Gain in potential energy (\(PE\)) as the lorry climbs the hill: \(PE = 15000 \times 10 \times 16 = 2,400,000 \, \text{J}\)
– Work done against resistance during the climb: \(WD = 1800 \times 1440 = 2,592,000 \, \text{J}\)
– Work done by the driving force (engine): \(Work = \Delta PE – WD = 2,400,000 – 2,592,000 = -192,000 \, \text{J}\)
(ii)
– Change in kinetic energy (\(\Delta KE\)) from the top of the hill to point P: \(\Delta KE = \text{Work} = 5030 \times 10^3 \, \text{J}\)
– Initial kinetic energy (\(KE_1\)) at the top of the hill is zero since the lorry’s speed is zero.
– Final kinetic energy (\(KE_2\)) at point P: \(\frac{1}{2}mv^2 = \frac{1}{2} \times 15,000 \times (24^2) = 4,320,000 \, \text{J}\)
\(\Delta KE = \text{Work}\)
\(4,320,000 – 0 = 5030 \times 10^3\)
\(5030 \times 10^3 = 4,320,000\)
The distance traveled from the top of the hill to point P:
\(5030 \times 10^3 = \frac{1}{2} \times 15,000 \times (24^2) + 1600d\)
\(5030 \times 10^3 = 4,320,000 + 1600d\)
\(1600d = 5030 \times 10^3 – 4,320,000\)
\(1600d = 610,000\)
\(d = \frac{610,000}{1600} = 1500 \, \text{m}\)
So, the distance from the top of the hill to point P is indeed 1500 meters.
Question
A car of mass 1250 kg travels from the bottom to the top of a straight hill of length 600 m, which is inclined at an angle of 2.5° to the horizontal. The resistance to motion of the car is constant and equal to 400 N. The work done by the driving force is 450 kJ. The speed of the car at the bottom of the hill is 30 m s−1. Find the speed of the car at the top of the hill.
▶️Answer/Explanation
The increase in potential energy (\(PE\)) as the car climbs the hill:
\(PE = mgh = 1250 \times 10 \times 600 \times \sin(2.5^\circ)\)
\(KE = \frac{1}{2}m(v_{\text{bottom}}^2 – \text{v}_{\text{top}}^2)\)
The work done against resistance (\(WD\)) during the climb:
\(WD = \text{Resistance} \times \text{Distance} = 400 \times 600\)
Apply the conservation of energy, where the increase in potential energy equals the sum of the decrease in kinetic energy and the work done against resistance:
\(PE = KE + WD\)
\(562500 – 625v_{\text{top}}^2 = 327145 + 240000\)
\(v_{\text{top}} = 26.7 \, \text{m/s}\)
The speed of the car at the top of the hill is indeed \(26.7 \, \text{m/s}\).
Question
A car of mass 1200 kg moves in a straight line along horizontal ground. The resistance to motion of the car is constant and has magnitude 960 N. The car’s engine works at a rate of 17 280 W.
(i) Calculate the acceleration of the car at an instant when its speed is 12 m\( s^{−1}\) The car passes through the points A and B. While the car is moving between A and B it has constant
speed V m\( s^{−1}\)
(ii) Show that V = 18.
At the instant that the car reaches B the engine is switched off and subsequently provides no energy. The car continues along the straight line until it comes to rest at the point C. The time taken for the
car to travel from A to C is 52.5 s.
(iii) Find the distance AC.
▶️Answer/Explanation
(i) Finding the acceleration (\(a\)) when the car’s speed is \(12 \, \text{m/s}\):
We use the equation of motion that relates force, mass, and acceleration:
\(F – R = ma\)
Where:
– \(F\) is the driving force (in this case, the engine’s power output).
– \(R\) is the resistance force (constant at \(960 \, \text{N}\)).
– \(m\) is the mass of the car (\(1200 \, \text{kg}\)).
– \(a\) is the acceleration.
Given that the engine’s power output is \(17280 \, \text{W}\), we can find the driving force using the equation for power:
\(P = F \cdot v\)
Where:
– \(P\) is power (\(17280 \, \text{W}\)).
– \(F\) is the driving force.
– \(v\) is the speed (\(12 \, \text{m/s}\)).
\(F = \frac{P}{v} = \frac{17280 \, \text{W}}{12 \, \text{m/s}} = 1440 \, \text{N}\)
Now, we can use this driving force in the equation of motion:
\(1440 \, \text{N} – 960 \, \text{N} = 1200 \, \text{kg} \cdot a\)
\(a = \frac{1440 \, \text{N} – 960 \, \text{N}}{1200 \, \text{kg}} = 0.4 \, \text{m/s}^2\)
(ii) Showing that \(V_m = 18 \, \text{m/s}\):
When the car is moving at constant speed (\(V_m\)), its acceleration (\(a\)) is zero. In this situation, the driving force is equal to the resistance force. So, we can write:
\(F – R = 0\)
\(F – 960 \, \text{N} = 0\)
\(P = F \cdot V_m\)
Given that \(P = 17280 \, \text{W}\), we can solve for \(V_m\):
\(17280 \, \text{W} = (960 \, \text{N}) \cdot V_m\)
\(V_m = \frac{17280 \, \text{W}}{960 \, \text{N}} = 18 \, \text{m/s}\)
(iii) Finding the distance \(AC\):
Since the car comes to rest at point C, it means that the work done by the engine (\(W_{\text{engine}}\)) is equal to the work done against resistance. We can use the work-energy principle:
\(W_{\text{engine}} = F_{\text{resistance}} \cdot d\)
Where:
– \(W_{\text{engine}}\) is the work done by the engine, equal to the engine’s power output multiplied by the time taken (\(P \cdot t\)).
– \(F_{\text{resistance}}\) is the resistance force (\(960 \, \text{N}\)).
– \(d\) is the distance from A to C.
\(P \cdot t = F_{\text{resistance}} \cdot d\)
\(17280 \, \text{W} \cdot 52.5 \, \text{s} = 960 \, \text{N} \cdot d\)
\(d = \frac{17280 \, \text{W} \cdot 52.5 \, \text{s}}{960 \, \text{N}} = 945 \, \text{m}\)
Therefore, the distance \(AC\) is \(945 \, \text{meters}\).
(iii) Using the kinematic equations for motion with constant acceleration:
For the segment BC, where the car decelerates from 18 m/s to 0 m/s:
\(a = -0.8 \, \text{m/s}^2\)
\(t_{BC} = \frac{0 \, \text{m/s} – 18 \, \text{m/s}}{-0.8 \, \text{m/s}^2} = 22.5 \, \text{s}\)
\(s_{BC} = \frac{0 \, \text{m/s} – (18 \, \text{m/s})^2}{-1.6 \, \text{m/s}^2} = 202.5 \, \text{m}\)
\(AB = 18 \, \text{m/s} \cdot (52.5 \, \text{s} – 22.5 \, \text{s}) = 540 \, \text{m}\)
\(AC = AB + BC = 540 \, \text{m} + 202.5 \, \text{m} = 742.5 \, \text{m}\)
Question
A car of mass 880 kg travels along a straight horizontal road with its engine working at a constant rate of P W. The resistance to motion is 700 N. At an instant when the car’s speed is 16 m \(s^{−1} \)its acceleration is 0.625 m\( s^{−2}\). Find the value of P.
▶️Answer/Explanation
To find the value of \(P\), we’ll use the equation for the net force acting on the car:
\(\text{Net Force} = \text{Driving Force} – \text{Resistance Force}\)
We know that the resistance to motion is \(700 \, \text{N}\), and we’ll denote the driving force as \(F_d\).
The driving force is related to power (\(P\)) and speed (\(v\)) by the formula:
\(P = F_d \cdot v\)
Since we have the speed (\(v = 16 \, \text{m/s}\)), we can calculate the driving force:
\(F_d = \frac{P}{v}\)
\(a = \frac{\text{Net Force}}{\text{Mass}}\)
\(0.625 \, \text{m/s}^2 = \frac{F_d – 700 \, \text{N}}{880 \, \text{kg}}\)
\(F_d = (0.625 \, \text{m/s}^2) \cdot (880 \, \text{kg}) + 700 \, \text{N}\)
\(F_d = 550 \, \text{N} + 700 \, \text{N} = 1250 \, \text{N}\]
Now that we have the driving force, we can calculate the power \(P\):
\(P = F_d \cdot v = 1250 \, \text{N} \cdot 16 \, \text{m/s} = 20,000 \, \text{Watts} = 20 \, \text{kW}\)
So, the power output of the car’s engine is \(20 \, \text{kW}\).
Question

A load of mass 160 kg is pulled vertically upwards, from rest at a fixed point O on the ground, using a winding drum. The load passes through a point A, 20 m above O, with a speed of \(1.25 m s^{−1}\)(see diagram). Find, for the motion from O to A,
(i) the gain in the potential energy of the load,
(ii) the gain in the kinetic energy of the load. The power output of the winding drum is constant while the load is in motion.
(iii) Given that the work done against the resistance to motion from O to A is 20 kJ and that the time taken for the load to travel from O to A is 41.7 s, find the power output of the winding drum.
▶️Answer/Explanation
(i) The Gain in Potential Energy (\(PE\)):
– Potential energy is the energy an object possesses due to its position relative to a reference point. In this case, the reference point is at the ground level, so when the load is lifted from the ground to point A, it gains potential energy.
– The formula for potential energy is \(PE = mgh\), where:
– \(PE\) is the potential energy gained.
– \(m\) is the mass of the load (160 kg).
– \(g\) is the acceleration due to gravity (approximately 9.81 m/s²).
– \(h\) is the change in height, which is the vertical distance the load is lifted. In this case, it’s 20 meters.
– Plugging in these values, we get \(PE = 160 \, \text{kg} \times 9.81 \, \text{m/s²} \times 20 \, \text{m} = 32,000 \, \text{Joules}\).
(ii) The Gain in Kinetic Energy (\(KE\)):
– Kinetic energy is the energy an object possesses due to its motion. As the load is lifted from the ground to point A, it gains kinetic energy because it is moving.
– The formula for kinetic energy is \(KE = \frac{1}{2}mv^2\), where:
– \(KE\) is the kinetic energy gained.
– \(m\) is the mass of the load (160 kg).
– \(v\) is the speed of the load. At point A, the speed is given as 1.25 m/s.
– Plugging in these values, we get
\(KE = \frac{1}{2} \times 160 \, \text{kg} \times (1.25 \, \text{m/s})^2 = 125 \, \text{Joules}\).
(iii) The work done (\(WD\)) by the drum is calculated as:
\(WD = PE_{\text{gain}} + KE_{\text{gain}} + \text{Work done against resistance}\)
\(WD = 32,000 \, \text{J} + 125 \, \text{J} + 20,000 \, \text{J} = 52,125 \, \text{J}\)
\(P = \frac{WD}{\text{time}}\)
Where \(WD\) is the work done (52,125 J) and the time is 41.7 s:
\(P = \frac{52,125 \, \text{J}}{41.7 \, \text{s}} \approx 1250 \, \text{W}\)
So, the power output of the winding drum is indeed \(1250 \, \text{W}\).