Question
A block B of mass 2.7 kg is pulled at constant speed along a straight line on a rough horizontal floor. The pulling force has magnitude 25 N and acts at an angle of θ above the horizontal. The normal component of the contact force acting on B has magnitude 20 N.
(i) Show that sin θ = 0.28.
(ii) Find the work done by the pulling force in moving the block a distance of 5 m.
▶️Answer/Explanation
(i) To show that \(\sin \theta = 0.28\)
The normal component of the contact force is 20N acting vertically upward. Therefore, the vertical component of the applied force \( F_{\text{vertical, applied}} \) must be equal to the gravitational force acting on the block 2.7g, where g is the acceleration due to gravity, approximately \(9.8m/s^2\):
\(F_{\text{vertical, applied}} = 2.7g.\)
The vertical component of the applied force can be expressed as:
\(F_{\text{vertical, applied}} = F_{\text{applied}} \sin \theta.\)
\(2.7g = 25 \sin \theta.\)
\(25 \sin \theta = 2.7g.\)
\(\sin \theta = \frac{2.7g}{25} \approx 0.28.\)
Therefore, \(\sin \theta = 0.28.\)
(ii) To find the work done by the pulling force in moving the block a distance of $5 \, \mathrm{m}$, we use the formula for work:
\( \text{Work} = \text{Force} \times \text{Distance} \times \cos \theta. \)
The force is $25 \, \mathrm{N}$, the distance is $5 \, \mathrm{m}$, and we have already calculated $\sin \theta = 0.28$, so $\cos \theta = \sqrt{1 – \sin^2 \theta} = \sqrt{1 – 0.28^2} = \sqrt{0.92}$.
\( \text{Work} = 25 \, \mathrm{N} \times 5 \, \mathrm{m} \times \sqrt{0.92} \approx 120 \, \mathrm{J}. \)
The correct work done by the pulling force in moving the block a distance of $5 \, \mathrm{m}$ is approximately 120J.
Question
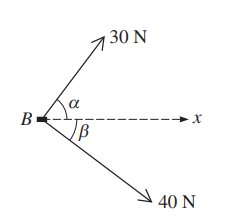
A block B lies on a rough horizontal plane. Horizontal forces of magnitudes 30 N and 40 N, making angles of α and β respectively with the x-direction, act on B as shown in the diagram, and B is moving in the x-direction with constant speed. It is given that cos α = 0.6 and cos β = 0.8.
(i) Find the total work done by the forces shown in the diagram when B has moved a distance of 20 m.
(ii) Given that the coefficient of friction between the block and the plane is \(\frac{5}{8}\) , find the weight of the block.
▶️Answer/Explanation
(i) To find the total work done by the forces shown in the diagram when the block B has moved a distance of 20 m, we need to consider the work done by each force separately and then sum them up.
The work done by a force is given by the formula:
\( \text{Work} = \text{Force} \times \text{Distance} \times \cos \theta \)
where
– Force is the magnitude of the force,
– Distance is the distance over which the force is applied, and
– θ is the angle between the force vector and the direction of motion.
Now, the work done by each force:
For the 30 N force (making an angle α with the x-direction, where $\cos \alpha = 0.6$):
\( \text{Work}_1 = 30 \, \mathrm{N} \times 20 \, \mathrm{m} \times \cos \alpha = 30 \, \mathrm{N} \times 20 \, \mathrm{m} \times 0.6 = 360 \, \mathrm{J} \)
For the 40 N force (making an angle β with the x-direction, where $\cos \beta = 0.8$):
\( \text{Work}_2 = 40 \, \mathrm{N} \times 20 \, \mathrm{m} \times \cos \beta = 40 \, \mathrm{N} \times 20 \, \mathrm{m} \times 0.8 = 640 \, \mathrm{J} \)
\( \text{Total Work} = \text{Work}_1 + \text{Work}_2 = 360 \, \mathrm{J} + 640 \, \mathrm{J} = 1000 \, \mathrm{J} \)
So, the total work done by the forces is 1000 J.
(ii) To find the weight of the block, we can use the information that the coefficient of friction between the block and the plane is $\frac{5}{8}$.
The frictional force ($F_{\text{friction}}$) can be calculated as:
\( F_{\text{friction}} = \text{Friction coefficient} \times \text{Normal force} \)
In this case, the normal force ($F_{\text{normal}}$) is equal to the weight of the block,
\( F_{\text{friction}} = \left(\frac{5}{8}\right) \times \text{Weight of the block} \)
We also know that the block is moving at a constant speed, which means there is no net force acting in the horizontal direction. The net force in the horizontal direction is zero.
The net force in the x-direction is the vector sum of the 30 N and 40 N forces. Since the block is moving at constant speed, the frictional force must be equal in magnitude and opposite in direction to the net force applied by the two forces.
\( F_{\text{friction}} = 30 \, \mathrm{N} \cos \alpha + 40 \, \mathrm{N} \cos \beta \)
\( \left(\frac{5}{8}\right) \times \text{Weight of the block} = 30 \, \mathrm{N} \cdot 0.6 + 40 \, \mathrm{N} \cdot 0.8 \)
\( \frac{5}{8} \times \text{Weight of the block} = 18 \, \mathrm{N} + 32 \, \mathrm{N} \)
\( \frac{5}{8} \times \text{Weight of the block} = 50 \, \mathrm{N} \)
\( \text{Weight of the block} = \frac{8}{5} \times 50 \, \mathrm{N} = 80 \, \mathrm{N} \)
So, the weight of the block is 80 N.
Question
The diagram shows the vertical cross-section ABCD of a surface. BC is a circular arc, and AB and CD are tangents to BC at B and C respectively. A and D are at the same horizontal level, and B and C are at heights 2.7 m and 3.0 m respectively above the level of A and D. A particle P of mass 0.2 kg is given a velocity of 8 m\( s^{−1}\) at A, in the direction of AB (see diagram). The parts of the surface containing AB and BC are smooth.
(i) Find the decrease in the speed of P as P moves along the surface from B to C.
The part of the surface containing CD exerts a constant frictional force on P, as it moves from C to
D, and P comes to rest as it reaches D.
(ii) Find the speed of P when it is at the mid-point of CD.
▶️Answer/Explanation
(i) Loss of Speed from B to C:
The calculation of the loss of speed from point B to C is based on the conservation of energy. The total mechanical energy of the particle is conserved as it moves along the path.
At point A, the particle has kinetic energy given by \(KE_A = \frac{1}{2}mv_A^2\) due to its initial velocity of \(8 \, \text{m/s}\).
As the particle moves from A to B, it gains gravitational potential energy, which is \(mg \cdot 2.7 \, \text{m}\). This energy comes at the expense of its kinetic energy. So, at point B, the kinetic energy is reduced, and we can write it as \(KE_B = KE_A – mg \cdot 2.7\).
At point C, the particle has lost further kinetic energy due to the gravitational potential energy it gained when moving from B to C, so \(KE_C = KE_B – mg \cdot 0.3\).
Now, we have two equations:
\(KE_B = \frac{1}{2}mv_B^2 = KE_A – mg \cdot 2.7\)
\(KE_C = \frac{1}{2}mv_C^2 = KE_B – mg \cdot 0.3\)
\(v_B^2 = 8^2 – 20 \cdot 2.7\)
\(v_C^2 = 8^2 – 20 \cdot 3\)
These equations give the squares of the speeds at B and C. To find the actual speeds, take the square root. The loss of speed is the difference between the speed at B and C, which is \(10^{1/2} – 2 = 1.16 \, \text{m/s}\).
(ii) To find the speed at the midpoint of CD, we again use the work-energy principle. The work done by the frictional force brings the particle to rest at point D. The work done is equal to the initial kinetic energy at point C:
\(W_{\text{friction}} = \frac{1}{2}mv_M^2\)
Where:
– \(v_M\) is the speed at the midpoint of CD.
– \(W_{\text{friction}}\) is the work done by the frictional force.
\(W_{\text{friction}} = \frac{1}{2}(0.4 + 6) \, \text{J} = 3.2 \, \text{J}\)
\(3.2 \, \text{J} = \frac{1}{2}(0.2)v_M^2\)
\(v_M^2 = \frac{3.2 \, \text{J}}{0.1 \, \text{kg}} = 32 \, \text{m}^2/\text{s}^2\)
\(v_M = \sqrt{32} \, \text{m/s} \approx 1.41 \, \text{m/s}\)
So, the speed at the midpoint of CD is approximately \(1.41 \, \text{m/s}\).