Question
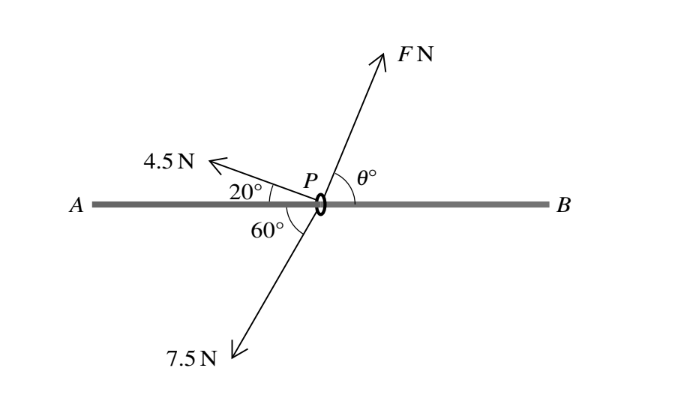
A small ring P is threaded on a fixed smooth horizontal rod AB. Three horizontal forces of magnitudes
4.5 N, 7.5 N and F N act on P (see diagram).
(i) Given that these three forces are in equilibrium, find the values of F and 1.
(ii) It is given instead that the values of F and 1 are 9.5 and 30 respectively, and the acceleration of
the ring is 1.5\( ms^{-2}\). Find the mass of the ring.
▶️Answer/Explanation
(i) Resolve forces either horizontally or vertically
7.5cos60+ 4.5cos20=Fcosθ [= 7.97861]
7.5sin60– 4.5sin20=Fsinθ [= 4.95609] \(f=\sqrt{(7.98^{2}+4.96^{2})}\) \(\Theta =tan^{-1}(\frac{4.96}{7.98})\)
F= 9.39 and θ = 31.8
Alternative method for question (i)
\(\frac{F}{sin80}=\frac{4.5}{sin(120+\Theta )}=\frac{7.5}{sin(160-\Theta )}\)
[4.5sin(160–θ) = 7.5sin(120+θ)]
Use the
θ value found by valid trigonometry to find F
= 9.39 and θ = 31.8
(i) Alternative method for question (i)
Forces 4.5, 7.5, F opposite angles 60 –θ, θ + 20, 100
\([f^{2}=4.5^{2}+7.5^{2}-2\times 4.5\times 7.5\times cos100]\)
\(\left [ \frac{9.39}{sin100} =\frac{4.5}{sin(60-\Theta)}=\frac{7.5}{sin(\Theta +20)}\right ]\)
F= 9.39 and θ = 31.8
(ii)\( 9.5\cos 30^{\circ}-7.5\cos 60^{\circ}-4.5\cos 20^{\circ}=m\times 1.51 \)
\(8.227-3.75-4.23=m\times 1.51\)
m=0.166kg
Question
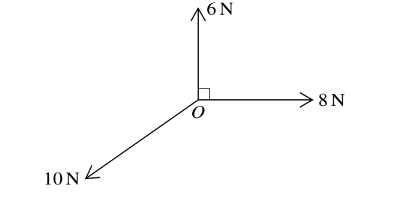
The diagram shows three coplanar forces acting at the point O. The magnitudes of the forces are 6 N, 8 N and 10 N. The angle between the 6 N force and the 8 N force is 90Å. The forces are in equilibrium. Find the other angles between the forces.
▶️Answer/Explanation
Using Lami’s Theorem
\(\Rightarrow \frac{10}{\sin 90^{\circ}}=\frac{6}{\sin (90^{\circ}+\alpha )}=\frac{8}{\sin(90+\beta ) }\)
\(\Rightarrow \frac{10}{\sin 90^{\circ}}=\frac{6}{\cos\alpha }=\frac{8}{\cos \beta }\)
\(\Rightarrow 10=\frac{6}{\cos\alpha }\) and \(10=\frac{8}{\cos \beta }\)
\(\Rightarrow \cos \alpha =\frac{6}{10}\) and \(\cos \beta =\frac{8}{10}\)
\(\Rightarrow \alpha =53.13^{\circ}\) and \(\Rightarrow \beta =36.86^{\circ}\)
Angle between 8N and 10N is \(\alpha =143.1\)
Angle between 6N and 10N is \(\beta =126.9\)
Question
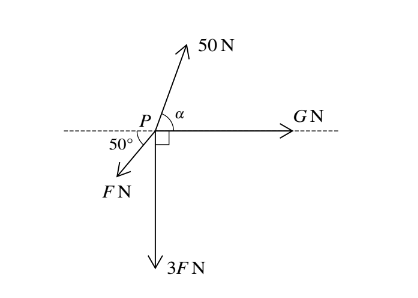
Coplanar forces, of magnitudes F N, 3F N, G N and 50 N, act at a point P, as shown in the diagram.
(i) Given that F = 0, G = 75 and\( \alpha= 60^{\circ}\), find the magnitude and direction of the resultant force.
(ii) Given instead that G = 0 and the forces are in equilibrium, find the values of F and\( \alpha\).
▶️Answer/Explanation
(i)\(\Rightarrow \sum F_{x}=75+50 \cos 60^{\circ} \)
\(=75+50\times \frac{1}{2} \)
=100N
\(\Rightarrow \sum F_{x}=50\sin 60^{\circ}\)
=43.30N
\(\Rightarrow F_{R}=\sqrt{F_{x}^{2}+F_{y}^{2}}\)
\(\Rightarrow F_{R}=\sqrt{100^{2}+43.30^{2}}\)
\(\Rightarrow F_{R}=109^{\circ}\)
Angle of Resultant Vector,say \(\alpha \)
Then,\(\tan \alpha =\frac{F_{y}}{F_{x}}\)
\(\tan \alpha =\frac{43.3}{100}\)
\(\tan \alpha =0.433\)
\(\alpha =\tan^{-1}(0.433)\)
\(\alpha =23.41^{\circ}\)
(ii)Forces are in equilibrium Hence,forces along x-direction and y-direction will be zero.
Now,
\(\sum F_{x}=0\)
\(50\cos \alpha -F\cos 50^{\circ}=0\)
\(50\cos \alpha =F\cos 50^{\circ}\)
\(\cos \alpha=\frac{F\cos 50^{\circ}}{50}\)
\(50\sin \alpha-3F-F\sin50^{\circ}= 0 \)
\(50\sin \alpha=3F +F\sin50^{\circ}\)
\(\sin \alpha=\frac{3F +F\sin50^{\circ}}{50}\)
\(tan\alpha =\frac{3F+Fsin50^{\circ}}{Fcos50^{\circ}}\)
\(\tan \alpha =\frac{3R+0.766F}{0.642F}\)
\(\tan \alpha =\frac{3.766F}{0.642F}\)
\(\alpha =\tan^{-1}80.3\)
\(\alpha =80.31^{\circ}\)
(a) Question
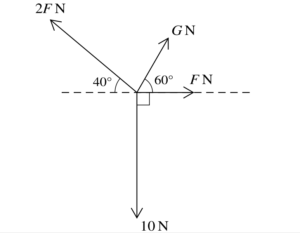
Four coplanar forces act at a point. The magnitudes of the forces are 10 N, F N, GN and 2F N. The directions of the forces are as shown in the diagram.
Given that the forces are in equilibrium, find the values of F and G.
▶️Answer/Explanation
For the system to be in equilibrium, the vector sum of all forces must be zero.
This means that the forces must balance each other out both vertically and horizontally.
(a)For vertical equilibrium, the upward forces must equal the downward forces. For horizontal equilibrium, the leftward forces must equal the rightward forces.
Breaking down the forces into their horizontal (x) and vertical (y) components.
The \( G \) N force has two components: \( G \sin(60^\circ) \) upward and \( G \cos(60^\circ) \) to the right.
The \( 2F \) N force has two components: \( 2F \sin(40^\circ) \) upward and \( 2F \cos(40^\circ) \) to the left.
For the vertical (y) components:
\( G \sin(60^\circ) + 2F \sin(40^\circ) = 10 \) (1)
For the horizontal (x) components:
\( F + G \cos(60^\circ) = 2F \cos(40^\circ) \) (2)
Now, let’s solve these equations for \( F \) and \( G \).
From equation (2):
\( F = 2F \cos(40^\circ) – G \cos(60^\circ) \)
\( F(1 – 2\cos(40^\circ)) = -G \cos(60^\circ) \). (3)
\( F + G \cos(60^\circ) = 2F \cos(40^\circ) \)
\( F(1 – 2\cos(40^\circ)) = -G \cos(60^\circ) \)
\( F(1 – 1.5320) = -0.5G \)
\( -0.5320F = -0.5G \)
\( G = 1.064F \) (5)
Substituting (5) into (1) for \( G \):
\( 1.064F \sin(60^\circ) + 2F \sin(40^\circ) = 10 \)
\( 1.064F \times 0.8660 + 2F \times 0.6428 = 10 \)
\( 0.9213F + 1.2856F = 10 \)
\( 2.2069F = 10 \)
\( F \approx \frac{10}{2.2069} \)
\( F \approx 4.53 \, \text{N} \)
Now,
\( G = 1.064 \times 4.53 \)
\( G \approx 4.53 \times 1.064 \)
\( G \approx 4.82 \, \text{N} \)
So, \( F \approx 4.53 \, \text{N} \) and \( G \approx 4.82 \, \text{N} \) when the forces are in equilibrium.
(b) Question
Given instead that F = 3, find the value of G for which the resultant of the forces is perpendicular to the 10 N force.
▶️Answer/Explanation
(b) For the resultant force to be perpendicular to the 10 N force, the horizontal components must add up to zero since the 10 N force is vertical.
The horizontal component of \( G \) is \( G \cos(60^\circ) = 0.5G \), and the horizontal component of \( 2F \) is \( 2F \cos(40^\circ) \).
\( 2F \cos(40^\circ) = 0.5G \)
\( 2 \times 3 \times 0.7660 = 0.5G \)
\( 4.596 = 0.5G \)
\( G = 9.192 \)
Hence, \( G \) is 9.19 N when \( F = 3 \) N and the resultant of the forces is perpendicular to the 10 N force.
Question
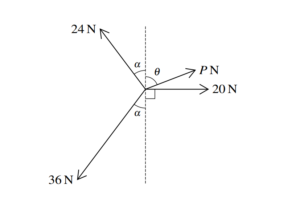
Coplanar forces of magnitudes 24 N, P N, 20 N and 36 N act at a point in the directions shown in the diagram. The system is in equilibrium.
Given that sin α = find the values of P and θ.
▶️Answer/Explanation
The horizontal force balance equation should be:
\( P \cos(\theta) = (36 – 24) \cos(36.9^\circ) \)
\( P \cos(\theta) = 12 \times 0.8 \)
\( P \cos(\theta) = 9.6 \) (1)
The vertical force balance equation should be:
\( P \sin(\theta) + 20 = (24 + 36) \sin(36.9^\circ) \)
\( P \sin(\theta) + 20 = 60 \times 0.6 \)
\( P \sin(\theta) = 36 – 20 \)
\( P \sin(\theta) = 16 \) (2)
From equations (1) and (2), we have two equations with two unknowns (\( P \) and \( \theta \)).
To find P, we can use the Pythagorean theorem:
\( P = \sqrt{(P \cos(\theta))^2 + (P \sin(\theta))^2} \)
\( P = \sqrt{9.6^2 + 16^2} \)
\( P = \sqrt{92.16 + 256} \)
\( P = \sqrt{348.16} \)
\( P = 18.66 \)
To find θ, we use the arctangent function
\( \theta = \tan^{-1}\left(\frac{P \sin(\theta)}{P \cos(\theta)}\right) \)
\( \theta = \tan^{-1}\left(\frac{16}{9.6}\right) \)
\( \theta \approx \tan^{-1}(1.6667) \)
\( \theta \approx 59.0^\circ \)
So the magnitude of force P is approximately 18.66 N, and the angle θ is approximately 59.0 degrees.
Question
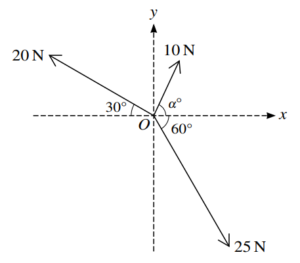
Three coplanar forces of magnitudes 10 N, 25 N and 20 N act at a point O in the directions shown in
the diagram.
(a) Given that the component of the resultant force in the x-direction is zero, find a, and hence find
the magnitude of the resultant force.
(b) Given instead that a = 45, find the magnitude and direction of the resultant of the three forces.
▶️Answer/Explanation
(a)Given that the x-component of the resultant force is zero,
\( 20 \cos(30^\circ) = 25 \cos(60^\circ) + 10 \cos(\alpha) \)
\( 17.32 = 12.5 + 10 \cos(\alpha) \)
\( 10 \cos(\alpha) = 4.82 \)
\( \cos(\alpha) = 0.482 \)
\( \alpha \approx 61.2^\circ \)
The resultant force using the y-components of the forces:
\( R = 20 \sin(30^\circ) + 10 \sin(61.2^\circ) – 25 \sin(60^\circ) \)
\( R = 10 + 8.761 – 21.651 \)
\( R \approx 2.89 \, N \)
(b) For the x-component:
\( X = 25 \cos(60^\circ) + 10 \cos(45^\circ) – 20 \cos(30^\circ) \)
\( X = 12.5 + 7.07107 – 17.32051 \)
\( X \approx 2.25056 \)
For the y-component:
\( Y = 20 \sin(30^\circ) + 10 \sin(45^\circ) – 25 \sin(60^\circ) \)
\( Y = 10 + 7.07107 – 21.65064 \)
\( Y \approx -4.57957 \)
The magnitude of the resultant force is then:
\( R = \sqrt{X^2 + Y^2} \)
\( R = \sqrt{2.25056^2 + (-4.57957)^2} \)
\( R \approx 5.10 \, N \)
\( \theta = \tan^{-1}\left(\frac{Y}{X}\right) \)
\( \theta = \tan^{-1}\left(\frac{-4.57957}{2.25056}\right) \)
\( \theta \approx -63.8^\circ \)
Hence, the direction is \( 63.8^\circ \) below the positive x-axis.
Question
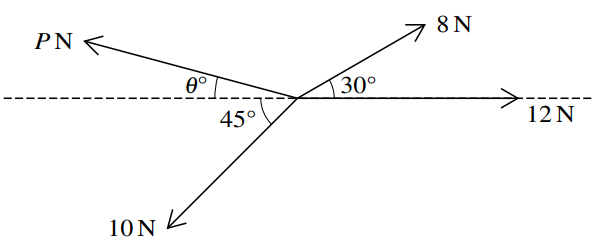
Coplanar forces of magnitudes 8 N, 12 N, 10 N and P N act at a point in the directions shown in the
diagram. The system is in equilibrium.
Find P and θ.
▶️Answer/Explanation
The 12 N force is purely horizontal and acts to the right.
The 8 N force has both horizontal and vertical components.
Horizontal component is \( 8 \cos(30^\circ) \).
Vertical component is \( 8 \sin(30^\circ) \).
The 10 N force is purely vertical.
The force \( P \) is at an angle \( \theta \) from the horizontal,
Its horizontal component is \( P \cos(\theta) \).
Its vertical component is \( P \sin(\theta) \).
Using these components, we can set up the equilibrium equations:
For horizontal equilibrium (taking right as positive and left as negative):
\( P \cos(\theta) – 8 \cos(30^\circ) = 12 \) …………..(1)
For vertical equilibrium (taking up as positive and down as negative):
\( 10 – 8 \sin(30^\circ) = P \sin(\theta) \) ……………(2)
From equation (1):
\( P \cos(\theta) = 12 + 8 \cos(30^\circ) \)
\( P \cos(\theta) = 12 + 8 \times \frac{\sqrt{3}}{2} \)
\( P \cos(\theta) = 12 + 4\sqrt{3} \)
\( P \cos(\theta) = 12 + 4 \times 1.732 \)
\( P \cos(\theta) \approx 12 + 6.928 \)
\( P \cos(\theta) \approx 18.928 \)
From equation (2):
\( P \sin(\theta) = 10 – 8 \times \frac{1}{2} \)
\( P \sin(\theta) = 10 – 4 \)
\( P \sin(\theta) = 6 \)
Now, \( \tan(\theta) = \frac{P \sin(\theta)}{P \cos(\theta)} \):
\( \tan(\theta) = \frac{6}{18.928} \)
\( \theta = \arctan\left(\frac{6}{18.928}\right) \)
\( \theta \approx \arctan(0.3168) \)
\( \theta \approx 17.68^\circ \)
\( P = \frac{6}{\sin(17.68^\circ)} \)
\( P \approx \frac{6}{0.304} \)
\( P \approx 19.74 \, N \)
Question
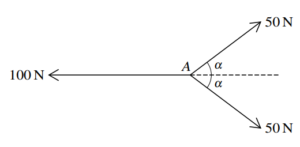
Three coplanar forces of magnitudes 100 N, 50 N and 50 N act at a point A, as shown in the diagram.
The value of cos \(\alpha \) is \(\frac{4}{5}\)
Find the magnitude of the resultant of the three forces and state its direction.
▶️Answer/Explanation
\(\cos \alpha = \frac{4}{5}\), and since \(\cos^2 \alpha + \sin^2 \alpha = 1\),
\(\sin \alpha = \sqrt{1 – \cos^2 \alpha} = \sqrt{1 – \left(\frac{4}{5}\right)^2} = \sqrt{1 – \frac{16}{25}} = \sqrt{\frac{9}{25}} = \frac{3}{5}\)
Now,
The 100 N force is purely horizontal.
The two 50 N forces have both horizontal and vertical components, given by:
\(\text{Horizontal component: } 50 \cos \alpha = 50 \times \frac{4}{5} = 40 \text{ N}\)
\(\text{Vertical component: } 50 \sin \alpha = 50 \times \frac{3}{5} = 30 \text{ N}\)
Since the two 50 N forces are symmetrical about point A, their horizontal components will cancel each other out, and their vertical components will add up.
Horizontal component (\(F_{\text{horizontal}}\)):
\(F_{\text{horizontal}} = 100 \text{ N} (left) + 40 \text{ N} (right) + 40 \text{ N} (right) = 100 \text{ N} – 80 \text{ N} = 20 \text{ N} \text{ (left)}\)
Vertical component (\(F_{\text{vertical}}\)):
\(F_{\text{vertical}} = 30 \text{ N} (up) + 30 \text{ N} (down) = 0 \text{ N} \text{ (since they cancel each other out)}\)
Therefore, the resultant force is purely horizontal and to the left, with a magnitude of 20 N.
Question
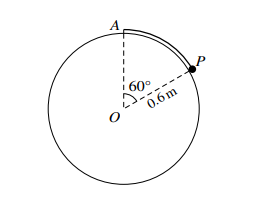
One end of a light inextensible string is attached to the highest point A of a solid fixed sphere with centre O and radius 0.6 m. The other end of the string is attached to a particle P of mass 0.2 kg which rests in contact with the smooth surface of the sphere. The angle AOP = 60° (see diagram). The sphere exerts a contact force of magnitude R N on P and the tension in the string is T N.
(i) By resolving vertically, show that R + (√3)T = 4.
P is now set in motion, and moves with angular speed ω rad s−1 in a horizontal circle on the surface of the sphere.
(ii) Find an equation involving R, T and ω.
(iii) Hence
(a) calculate R when ω = 2,
(b) find the greatest possible value of T and the corresponding speed of P.
Answer/Explanation

Question
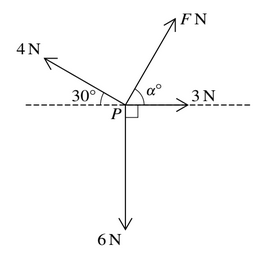
Coplanar forces, of magnitudes FN, 3N, 6N and 4N, act at a point P, as shown in the diagram.
(a) Given that \(\alpha=60\), and that the resultant of the four forces is in the direction of the 3N force, find F.
(b) Given instead that the four forces are in equilibrium, find the values of F and \(\alpha\).
▶️Answer/Explanation
Resolving the forces vertically and horizontally.
(a) Given that \(\alpha = 60^\circ\), we need to find the force \( F \) such that the resultant of the four forces is in the direction of the 3 N force.
\( 4 \sin(30^\circ) + F \sin(60^\circ) – 6 = 0 \)
Using the fact that \(\sin(30^\circ) = \frac{1}{2}\) and \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\),
\( 4 \times \frac{1}{2} + F \times \frac{\sqrt{3}}{2} – 6 = 0 \)
\( 2 + F \frac{\sqrt{3}}{2} – 6 = 0 \)
\( F \frac{\sqrt{3}}{2} = 4 \)
\( F = \frac{4}{\frac{\sqrt{3}}{2}} \)
\( F = \frac{4}{0.866} \)
\( F \approx 4.62 \, N \)
So, \( F \) is approximately 4.62 N.
(b) Given that the forces are in equilibrium, the sum of the forces in both the horizontal and vertical directions must be zero.
\( F \cos(\alpha) + 3 – 4 \cos(30^\circ) = 0 \)
\( 4.62 \cos(\alpha) + 3 – 4 \times \frac{\sqrt{3}}{2} = 0 \)
\( 4.62 \cos(\alpha) + 3 – 3.46 = 0 \)
\( 4.62 \cos(\alpha) = 0.46 \)
\( \cos(\alpha) = \frac{0.46}{4.62} \)
\( \cos(\alpha) \approx 0.1 \)
And vertically:
\( F \sin(\alpha) + 4 \sin(30^\circ) – 6 = 0 \)
\( 4.62 \sin(\alpha) + 4 \times \frac{1}{2} – 6 = 0 \)
\( 4.62 \sin(\alpha) + 2 – 6 = 0 \)
\( 4.62 \sin(\alpha) = 4 \)
\( \sin(\alpha) = \frac{4}{4.62} \)
\( \sin(\alpha) \approx 0.866 \)
\( (F \cos(\alpha))^2 + (F \sin(\alpha))^2 = F^2 \)
\( (0.46)^2 + (4)^2 = (4.62)^2 \)
\( \tan(\alpha) = \frac{F \sin(\alpha)}{F \cos(\alpha)} \)
\( \alpha = \tan^{-1}\left(\frac{4}{0.46}\right) \)
\( \alpha = \tan^{-1}\left(\frac{4}{0.46}\right) \)
\( \alpha \approx \tan^{-1}(8.696) \)
\( \alpha \approx 83.4^\circ \)
So, \( F \) is approximately 4.62 N and \( \alpha \) is approximately 83.4 degrees when the forces are in equilibrium.
Question
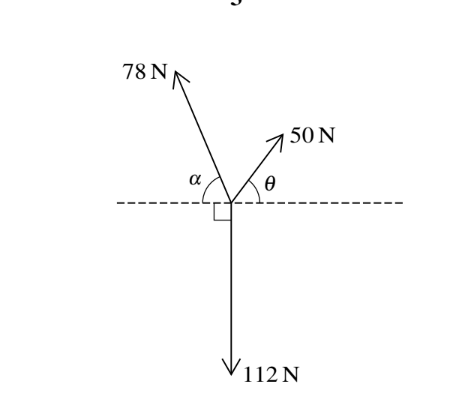
Given that\( tan\alpha =\frac{12}{5} \) and\( tan\Theta =\frac{4}{3}\),show that the coplanar forces shown in the diagram are in equilibrium.
Answer/Explanation
(X =) \(78× 5/13 – 50×3/5=78 cos 67.4 – 50 cos 53.1(Y =) 78× 12/13+ 50 × 4/5 – 112= 78 sin 67.4+ 50 sin 53.1 –112\)
[X = 30 – 30 = 0
Y = 72 + 40 – 112 = 0]
X = 0 andY =0
\(\frac{112}{sin59.5}\)=\(\frac{50}{sin157.5}\)=\(\frac{78}{sin143.1}
\frac{112}{\frac{56}{65}}\)=\(\frac{50}{\frac{5}{13}}\)=\(\frac{78}{\frac{3}{5}}\)=130
Question
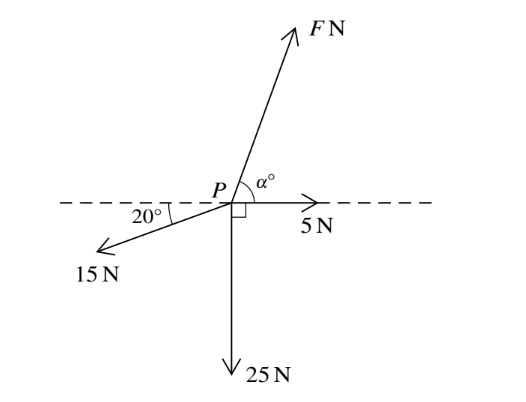
Four coplanar forces of magnitudes F N, 5 N, 25 N and 15 N are acting at a point P in the directions shown in the diagram. Given that the forces are in equilibrium, find the values of F and\( \alpha\)
▶️Answer/Explanation
Given that the forces are in equilibrium, the sum of the horizontal components must equal zero and the sum of the vertical components must also equal zero.
Horizontal Equilibrium:
For the 15 N force acting at a \( 20^\circ \) angle from the horizontal, its horizontal component is:
\( 15 \cos(20^\circ) \)
The horizontal component of force \( F \) is:
\( F \cos(\alpha) \)
The 5 N force contributes only to the vertical component, so it is not included in the horizontal equilibrium.
Setting the sum of horizontal components to zero:
\( F \cos(\alpha) = 15 \cos(20^\circ) \)
\[ F \cos(\alpha) = 15 \times 0.9397 \approx 14.0955 \] (rounded to 5 decimal places)
Vertical Equilibrium:
For the 15 N force, the vertical component is:
\( 15 \sin(20^\circ) \)
The vertical component of force \( F \) is:
\( F \sin(\alpha) \)
Including the 25 N force acting downwards and the 5 N force acting upwards, the sum of vertical components is set to zero:
\( F \sin(\alpha) = 25 – 5 – 15 \sin(20^\circ) \)
\( F \sin(\alpha) = 20 – 15 \times 0.3420 \approx 14.87 \) (rounded to 2 decimal places)
\( F = \sqrt{(15 \cos(20^\circ) – 5)^2 + (15 \sin(20^\circ) + 25)^2} \)
\( F = \sqrt{(15 \times 0.9397 – 5)^2 + (15 \times 0.3420 + 25)^2} \)
\( F = \sqrt{(14.0955 – 5)^2 + (5.13 + 25)^2} \)
\( F = \sqrt{(9.0955)^2 + (30.13)^2} \)
\( F = \sqrt{82.7280 + 907.8169} \)
\( F = \sqrt{990.5449} \)
\( F \approx 31.48 \) (rounded to 2 decimal places)
Now
\( \alpha = \tan^{-1}\left(\frac{15 \sin(20^\circ) + 25}{15 \cos(20^\circ) – 5}\right) \)
\( \alpha = \tan^{-1}\left(\frac{5.13 + 25}{14.0955 – 5}\right) \)
\( \alpha = \tan^{-1}\left(\frac{30.13}{9.0955}\right) \)
\[ \alpha \approx \tan^{-1}(3.3123) \)
\( \alpha \approx 73.1^\circ \) (rounded to 1 decimal place)
Question
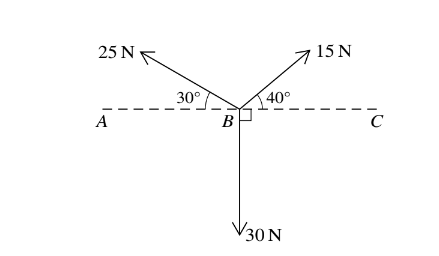
Coplanar forces, of magnitudes 15 N, 25 N and 30 N, act at a point B on the line ABC in the directions
shown in the diagram.
(i) Find the magnitude and direction of the resultant force.
(ii) The force of magnitude 15 N is now replaced by a force of magnitude F N acting in the same
direction. The new resultant force has zero component in the direction BC. Find the value of F, and find also the magnitude and direction of the new resultant force.
Answer/Explanation
(i) 25 cos 30
– 15 cos 40 (= 10.1599…)
25 sin 30+ 15 sin 40 – 30 (= –7.8581…)
Magnitude = \(\sqrt{(10.15..^{2}+7.858..^{2})}=12.8N= 12.8 N\)
Angle 37.7° below the horizontal in the direction BA
(ii) F cos 40= 25 cos 30
F = 28.3
New resultant force
= 28.26…sin 40+ 25 sin 30–30= 0.667 N upwards
Question
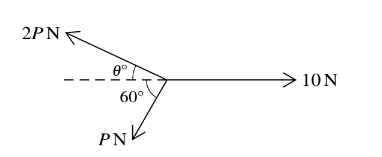
The three coplanar forces shown in the diagram are in equilibrium. Find the values of 1 and P.
Answer/Explanation
EITHER:
2P sin θ = P sin 60
θ = 25.7
2P cos θ + P cos 60 = 10
P = 4.34
θ = 25.7
Use a second Lami equation
P = 4.34
OR2:
Use sine or cosine rule with triangle of forces
using forces P, 2P and 10 and with angles 60,
θ and 120 – θ between
θ = 25.7
Use a second relationship from the triangle of
forces
P = 4.34
Question
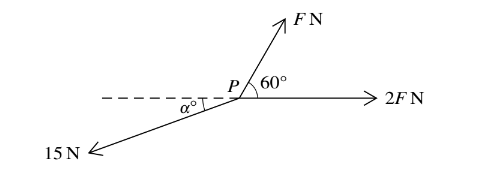
Three coplanar forces of magnitudes F N, 2F N and 15 N act at a point P, as shown in the diagram. Given that the forces are in equilibrium, find the values of F and\( \alpha.\)
Answer/Explanation
2F + Fcos60 = 15cosα
Fsin60 = 15sinα
F = 5.67 and α = 19.1
Question
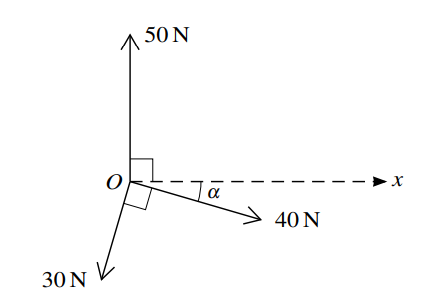
Coplanar forces of magnitudes 50 N, 40 N and 30 N act at a point O in the directions shown in the diagram, where tan \(\alpha = \frac{7}{24}\) .
(i) Find the magnitude and direction of the resultant of the three forces. [6]
(ii) The force of magnitude 50 N is replaced by a force of magnitude P N acting in the same direction. The resultant of the three forces now acts in the positive x-direction. Find the value of P. [1]
Answer/Explanation


Question
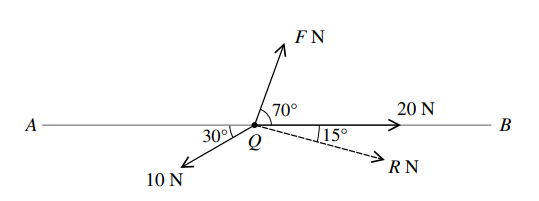
A small bead Q can move freely along a smooth horizontal straight wire AB of length 3 m. Three horizontal forces of magnitudes F N, 10 N and 20 N act on the bead in the directions shown in the diagram. The magnitude of the resultant of the three forces is R N in the direction shown in the diagram.
(i) Find the values of F and R. [5]
(ii) Initially the bead is at rest at A. It reaches B with a speed of 11.7 m s−1. Find the mass of the bead. [3]
Answer/Explanation
Ans:
(i) Fcos70 + 20 – 10 cos 30
= Rcos15
10sin30 – F sin70 = R sin15
F = 1.90 N and R = 12.4 N
Alternative method for (i)
[X = 0.342 F + 11.34
Y = 0.94 F – 5]
(0.342 F + 11.34)2 + (0.94 F – 5)2
= R2
tan15
= (5 – 0.94F) / (0.342F + 11.34)
F = 1.90 N and R = 12.4 N
(ii) 11.72 = 0 + 2a × 3
a = 22.815
R cos15 = m × 22.815
Mass of bead = 0.526 kg
Question
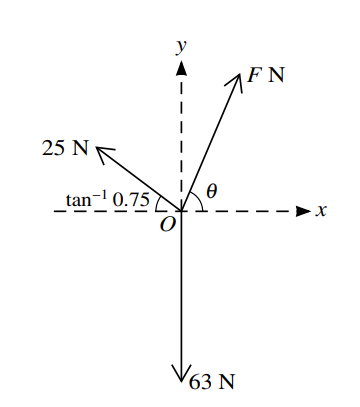
Three horizontal forces of magnitudes F N, 63 N and 25 N act at O, the origin of the x-axis and y-axis. The forces are in equilibrium. The force of magnitude F N makes an angle θ anticlockwise with the positive x-axis. The force of magnitude 63 N acts along the negative y-axis. The force of magnitude 25 N acts at tan−1 0.75 clockwise from the negative x-axis (see diagram). Find the value of F and the value of tan 1. [5]
Answer/Explanation
Fx = F cosθ = 25 × 0.8 = 20,
Fy = F sinθ = 63 – 25 × 0.6 = 48
F = 52 N or tanθ = 2.4
tanθ = 2.4 or F = 52 N
Question
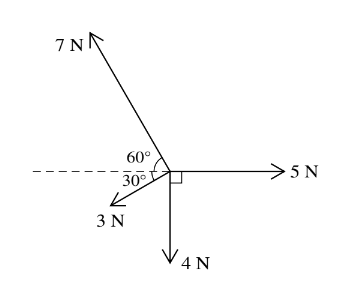
Four coplanar forces act at a point. The magnitudes of the forces are 5 N, 4 N, 3 N and 7 N, and the directions in which the forces act are shown in the diagram. Find the magnitude and direction of the resultant of the four forces
Answer/Explanation
.
X = 5 – 7cos 60o – 3cos 30o
(= – 1.098)
Y = 7sin 60o– 3sin 30o – 4 (= 0.5622)
Resultant is 1.23 N and
Direction is 152.9o
anticlockwise from
+ve x-axis oe
Question
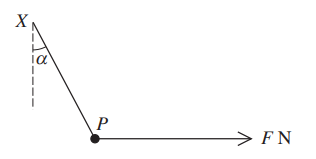
A particle P of mass 0.3 kg is attached to one end of a light inextensible string. The other end of the string is attached to a fixed point X. A horizontal force of magnitude F N is applied to the particle, which is in equilibrium when the string is at an angle α to the vertical, where tan α = \(\frac{8}{15}\) (see diagram). Find the tension in the string and the value of F. [4]
Answer/Explanation
[Tcosα = mg]
Tension is 3.4 N
[F = Tsinα]
F = 1.6
Question
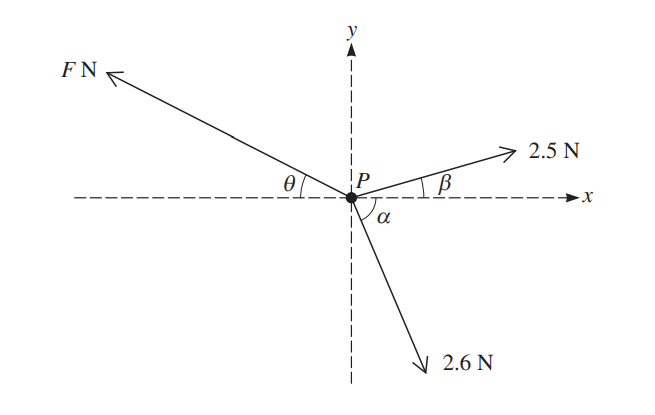
A particle P of mass 0.5 kg lies on a smooth horizontal plane. Horizontal forces of magnitudes F N,
2.5 N and 2.6 N act on P. The directions of the forces are as shown in the diagram, where tan \(\alpha =\frac{12}{5}\) and tan \(\beta =\frac{7}{24}\).
(i) Given that P is in equilibrium, find the values of F and tan θ. [6]
(ii) The force of magnitude F N is removed. Find the magnitude and direction of the acceleration with which P starts to move. [3]
Answer/Explanation
Ans:


Question
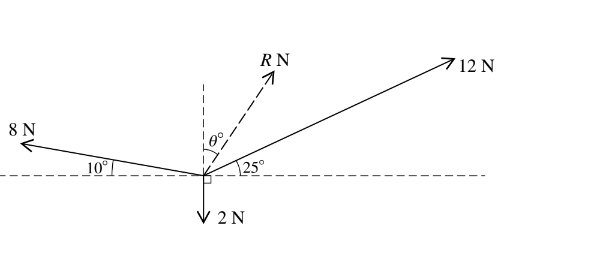
Three coplanar forces of magnitudes 8 N, 12 N and 2 N act at a point. The resultant of the forces has magnitude R N. The directions of the three forces and the resultant are shown in the diagram. Find R and θ.
Answer/Explanation
X = 12cos25o – 8cos10o (= 2.9972….)
Y = 12sin25o + 8sin10o – 2 (= 4.4606….)
R = 5.37
θ = 33.9
Question
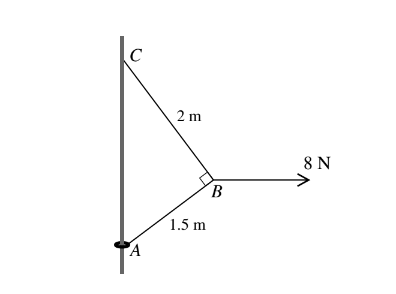
A small ring of mass 0.2 kg is threaded on a fixed vertical rod. The end A of a light inextensible string
is attached to the ring. The other end C of the string is attached to a fixed point of the rod above A. A horizontal force of magnitude 8 N is applied to the point B of the string, where AB = 1.5 m and BC = 2 m. The system is in equilibrium with the string taut and AB at right angles to BC (see diagram).
(i) Find the tension in the part AB of the string and the tension in the part BC of the string. The equilibrium is limiting with the ring on the point of sliding up the rod.
(ii) Find the coefficient of friction between the ring and the rod.
Answer/Explanation
(i)
\(T_{C}\) × (2/2.5) –\( T_{A} \)× (1.5/2.5) = 0
\(T_{C}\) × (1.5/2.5) +\( T_{A}\) × (2/2.5) = 8
[0.6 TC + 0.8\( (4T_{C}/3)\) = 8 → (5/3) TC = 8 or
0.6(0.75TA) + \(0.8T_{A} \)= 8 → \(1.25T_{A}\) = 8 ]
Tension in AB is 6.4 N; tension in BC is 4.8 N
(ii)
F + 0.2 g =\( T_{A}\) × (1.5/2.5) N = TA × (2/2.5)
[ μ = (3.84 – 2 )/5.12]
horizontal Coefficient is 0.359