Question
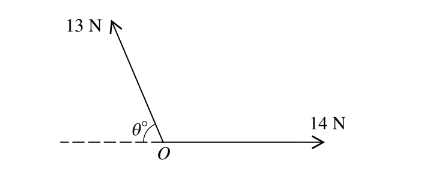
Forces of magnitudes 13 N and 14 N act at a point O in the directions shown in the diagram. The resultant of these forces has magnitude 15 N. Find
(i) the value of θ,
(ii) the component of the resultant in the direction of the force of magnitude 14 N.
▶️Answer/Explanation
(i) Using the law of cosines,
\(c^2 = a^2 + b^2 – 2ab \cos(θ)\)
where:
\(c\) is the magnitude of the resultant vector (15 N).
\(a\) is the magnitude of the 13 N force (13 N).
\(b\) is the magnitude of the 14 N force (14 N).
Now,
\(15^2 = 13^2 + 14^2 – 2(13)(14) \cos(θ)\)
\(225 = 169 + 196 – 364 \cos(θ)\)
\(225 = 365 – 364 \cos(θ)\)
\(364 \cos(θ) = 365 – 225\)
\(364 \cos(θ) = 140\)
\(\cos(θ) = \frac{140}{364}\)
\(θ = \arccos\left(\frac{140}{364}\right)\)
\(θ ≈ 58.73°\)
(ii) The component of the resultant in the direction of the 14 N force \(F_{14}\).
\(F_{14} = 15 \cos(θ)\)
Plug in the value of θ:
\(F_{14} = 15 \cos(58.73°)\)
\(F_{14} ≈ 9 \, \text{N}\)
So, the component of the resultant in the direction of the 14 N force is approximately 9N.