At a summer camp an arithmetic test is taken by 250 children. The times taken, to the nearest minute, to complete the test were recorded. The results are summarised in the table.
| Time taken, in minutes | 1-30 | 31-45 | 46-65 | 66-75 | 76-100 |
| Frequency | 21 | 30 | 68 | 86 | 45 |
(a) Question
Draw a histogram to represent this information.

Answer/Explanation
Ans:
| Class Width | 30 | 15 | 20 | 10 | 25 |
| Frequency Density | 0.7 | 2 | 3.4 | 8.6 | 1.8 |
(b) Question
State which class interval contains the median.
Answer/Explanation
Ans:
66 – 75
(c) Question
Given that an estimate of the mean time is 61.05 minutes, state what feature of the distribution accounts for the median and the mean being different.
Answer/Explanation
Ans:
Distribution is not symmetrical
Question
The random variable X takes the values 1, 2, 3, 4 only. The probability that X takes the value x is kx(5-x), where k is a constant.
(a) Draw up the probability distribution table for X, in terms of k.
(b) Show that Var(X)=1.05.
Answer/Explanation
Ans:
(a)
x | 1 | 2 | 3 | 4 |
| prob | 4k | 6k | 6k | 4k |
(b) \([4k+6k+6k+4k=1]k=\frac{1}{20}(=0.05)\)
\(E(X)=1\times \frac{4}{20}+2 \times \frac{6}{20}+3\times \frac{6}{20}+4\times \frac{4}{20}=\frac{4}{20}+\frac{12}{20}+\frac{18}{20}+\frac{16}{20}\)
\(Var(X)=1^2\times \frac{4}{20}+2^2\times \frac{6}{20}+3^2\times \frac{6}{20}+4^2 \times \frac{4}{20}-(their2\frac{1}{2})^2\)
\(=(4+24+54+64)\times their 0.05-(their2.5)^2\)
Or
\((1-2.5)^2\times \frac{4}{20}+(2-2.5)^2\times \frac{6}{20}+(3-2.5)^2\times \frac{6}{20}+(4-2.5)^2\times \frac{4}{20}\)
1.05
Question 4.
4 A survey was made of the journey times of 63 people who cycle to work in a certain town. The results are summarised in the following cumulative frequency table.

(i) State how many journey times were between 25 and 45 minutes. [1]
(ii) Draw a histogram on graph paper to represent the data. [4]
(iii) Calculate an estimate of the mean journey time. [2]
Answer/Explanation
Ans:
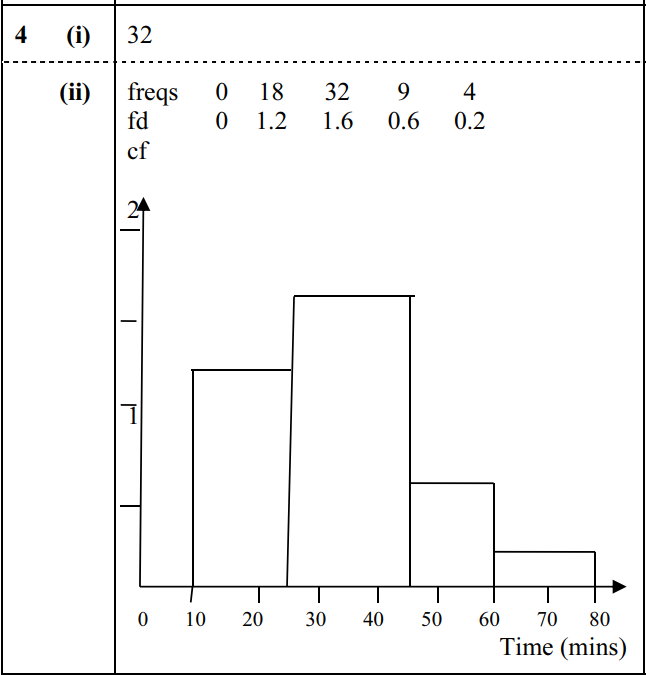
Question
Helen measures the lengths of 150 fish of a certain species in a large pond. These lengths, correct to the nearest centimetre, are summarised in the following table.
| Length(cm) | 0-9 | 10-14 | 15-19 | 20-30 |
| Frequency | 15 | 48 | 66 | 21 |
(a) Draw a cumulative frequency graph to illustrate the data.
(b) 40% of these fish have of d cm or more. Use your graph to estimate the value of d.
The mean length of these 150 fish is 15.295 cm.
(c) Calculate an estimate for the variance of the lengths of the fish.
Answer/Explanation
Ans:
(a) 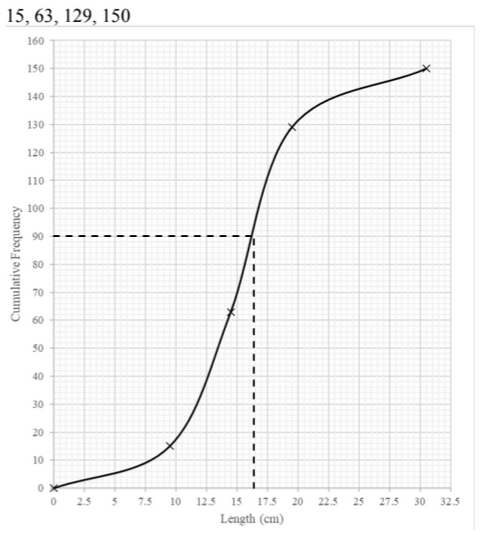
(b) 60% of 150 = 90
Approx. 16.5 [cm]
(c) Midpoints: 4.75, 12, 17, 25
Var = \(4.75^2 \times 15 + 12^2 \times 48 + 17^2 \times 66 + 25^2 \times 21}{150}-15.295^2\)
= 29.1
Question
For 10 values of x the mean is 86.2 and Σ(x − a) = 362. Find the value of
(i) Σ x, [1]
(ii) the constant a. [2]
Answer/Explanation
Ans:
1 (i) Σx = 862
(ii) 362/10 + a = 86.2
a = 50
Question
The numbers of chocolate bars sold per day in a cinema over a period of 100 days are summarised in
the following table.

(a) Draw a histogram to represent this information. [5]

(b) What is the greatest possible value of the interquartile range for the data? [2]
(c) Calculate estimates of the mean and standard deviation of the number of chocolate bars sold. [4]
Answer/Explanation
Ans
7 (a) Class widths: 10, 5, 15, 20, 10
Frequency density = frequency/their class width: 1.8, 4.8, 2, 1, 0.8
All heights correct on diagram (using a linear scale)
Correct bar ends
Bar ends: 10.5, 15.5, 30.5, 50.5, 60.5
7 (b) 11 – 15 and 31 – 50 B1
Greatest IQR = 50 – 11 = 39
7 (c) \(Mean=\frac{18\times 5.5+24\times 13+30\times 23+20\times 40.5+8\times 55.5}{100}=\frac{2355}{100}=23.6\)
\(Var=\frac{18\times 5.5^{2}+24\times 13^{2}+30\times 23^{2}+20\times 40.5^{2}+8\times 55.5^{2}}{100}-mean^{2}\)
\(\frac{77917.5}{100}-mean^{2}=224.57\)
Standard deviation = 15.0
(FT their variance)
Question
Richard has 3 blue candles, 2 red candles and 6 green candles. The candles are identical apart from their colours. He arranges the 11 candles in a line.
(a) Find the number of different arrangements of the 11 candles if there is a red candle at each end.
(b) Find the number of different arrangements of the 11 candles if all the blue candles are together and the red candles are not together.
Answer/Explanation
Ans:
(a) R^^^^^^^^^R
\(\frac{9!}{3!6!}\)
= 84
(b) ^(BBB)^^^^^
\(\frac{7!}{6!} \times \frac{8 \times 7}{2}\)
= 196
Alternative for question 4(b)
[Arrangements, blue together – Arrangements with blues together and reds together=]
\(\frac{9!}{2!6!}-\frac{8!}{6!}\}
= [252 – 56]
= 196
A summary of 40 values of x gives the following information:
Σ (x – k) = 520, Σ ( x – k)2 = 9640,
where k is a constant.
(a) Question
Given that the mean of these 40 values of x is 34, find the value of k.
Answer/Explanation
Ans:
\(\left [ \frac{\sum x}{40} – k = \frac{\sum (x-k)}{40}\right ]\)
\(\frac{40 \times 34}{40} – k = \frac{520}{40}\)
k [= 34 – 13] = 21
(b) Question
Find the variance of these 40 values of x.
Answer/Explanation
Ans:
\(Var = \left [ \frac{\sum (x – k)^{2}}{40} – (\frac{\sum (x – k)^{}}{40})^{2} \right ] = \frac{9640}{40} – \left ( \frac{520}{40} \right )^{2} = [241 – 13^{2} =]\)
72
The times, in minutes, that Karli spends each day on social media are normally distributed with mean 125 and standard deviation 24.
(a) (i) Question
On how many days of the year (365 days) would you expect Karli to spend more than 142 minutes on social media?
Answer/Explanation
Ans:
\(P(X>142) = P\left ( Z>\frac{142-125}{24} \right )\)
[=P(Z>0.7083) = ] 1-0.7604
0.2396
Their 0.2396 × 365 [=87.454]
87 or 88
(ii) Question
Find the probability that Karli spends more than 142 minutes on social media on fewer than 2 of 10 randomly chosen days.
Answer/Explanation
Ans:
P(0, 1) = 0.760410 + 10C1 × 0.23961 × 0.76049
[ = 0.064628 + 0.20364]
0.268
(b) Question
On 90% of days, Karli spends more than t minutes on social media.
Find the value of t.
Answer/Explanation
Ans:
z = ±1.282
\(\frac{t – 125}{24} = -1.282\)
t = 94.2
Question
The times, t minutes, taken by 150 students to complete a particular challenge are summarised in the
following cumulative frequency table.

(a) Draw a cumulative frequency graph to illustrate the data. [2]

(b) 24% of the students take k minutes or longer to complete the challenge. Use your graph to
estimate the value of k. [2]
(c) Calculate estimates of the mean and the standard deviation of the time taken to complete the
challenge. [6]
Answer/Explanation
Ans
6 (a) 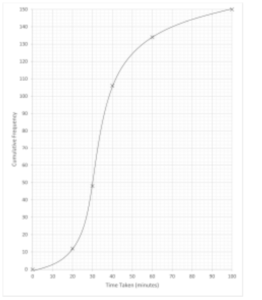
Correct cumulative frequency curve
6 (b) 150× 0·76 = 114
k = 45 (mins)
6 (c) Frequencies: 12 36 58 28 16
\(Mean=\frac{10\times 12 \times 25 \times 36\times 35\times 58 \times 50 \times 28\times 80\times 16}{150}\)
\(\frac{120 + 900 + 2030+ 1400 + 1280}{150}\)
\(38.2, 38\frac{1}{5}\)
\(Variance=\frac{12\times 10^{2}\times 36\times 25^{2}\times 58\times 35^{2}\times 28\times 50^{2}\times 16\times 80^{2}}{150}-mean^{2}\)
\(=\frac{1200 + 22500 + 71050 + 70000 + 102400}{150}-mean^{2}\)
(Standard deviation \(=\sqrt{321.76}=17.9\)
Question
The score when two fair six-sided dice are thrown is the sum of the two numbers on the upper faces.
(a) Show that the probability that the score is 4 is \(\frac{1}{12}\) [1]
The two dice are thrown repeatedly until a score of 4 is obtained. The number of throws taken is
denoted by the random variable X.
(b) Find the mean of X. [1]
(c) Find the probability that a score of 4 is first obtained on the 6th throw. [1]
(d) Find P(X < 8). [2]
Answer/Explanation
Ans
1 (a) Prob of 4 (from 1,3, 3,1 or 2,2) \(=\frac{3}{36}=\frac{1}{12} \ AG\)
1 (b) \(Mean=\frac{1}{\frac{1}{12}}=12\)
1 (c) \(\left ( \frac{11}{12} \right )\times \frac{1}{12}=0.0539\ or \frac{161051}{2985984}\)
1 (d) \(1-\left ( \frac{11}{12} \right )^{7}\)
\(0.456\ or \ \frac{16344637}{35831808}\ )