Question
The 40 members of a club include Ranuf and Saed. All 40 members will travel to a concert. 35 members will travel in a coach and the other 5 will travel in car. Ranuf will be in the coach and saed will be in the car.
In how many ways can the members who will travel in the coach be chosen?
Answer/Explanation
Ans:
\(^{38}C_t\) or \(^nC_{34}\)
\(^{38}C_{34}\)
73815
A factory produces chocolates in three flavours: lemon, orange and strawberry in the ratio 3 : 5 : 7 respectively. Nell checks the chocolates on the production line by choosing chocolates randomly one at a time.
(a) Question
Find the probability that the first chocolate with lemon flavour that Nell chooses is the 7th chocolate that she checks.
Answer/Explanation
Ans:
\(\left [ Probability of lemon = \frac{3}{15} = \frac{1}{5}\right ]\)
\(\left [ \left ( \frac{4}{5} \right )^{6} \times \frac{1}{5}\right ]\frac{4096}{78125}, 0.0524\)
(b) Question
Find the probability that the first chocolate with lemon flavour that Nell chooses is after she has checked at least 6 chocolates.
‘Surprise’ boxes of chocolates each contain 15 chocolates: 3 are lemon, 5 are orange and 7 are strawberry.
Petra has a box of Surprise chocolates. She chooses 3 chocolates at random from the box. She eats each chocolate before choosing the next one.
Answer/Explanation
Ans:
\(\left ( 1-\frac{1}{5} \right )^{6}\)
\(\frac{4096}{15625}, 0.262\)
(c) Question
Find the probability that none of Petra’s 3 chocolates has orange flavour.
Answer/Explanation
Ans:
\(\frac{10}{15}\times \frac{9}{14}\times \frac{8}{13}\)
\(\frac{24}{91}, 0.264\)
(d) Question
Find the probability that each of Petra’s 3 chocolates has a different flavour.
Answer/Explanation
Ans:
\(\frac{7}{15}\times \frac{5}{14}\times \frac{3}{13}\times 3!\)
\(\frac{3}{13}, 0.231\)
(e) Question
Find the probability that at least 2 of Petra’s 3 chocolates have strawberry flavour given that none of them has orange flavour.
Answer/Explanation
Ans:
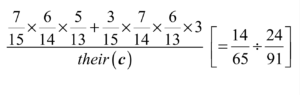
\(\frac{49}{60}, 0.817\)
Question
A fair eight-sided die has faces marked 1, 2, 3, 4, 5, 6, 7, 8. The score when the die is thrown is the number on the face the die lands on. The die is thrown twice.
- Event R is ‘one of the scores is exactly 3 greater than the other score’.
- Event S is ‘the product of the scores is more than 19’.
(i) Find the probability of R. [2]
(ii) Find the probability of S. [2]
(iii) Determine whether events R and S are independent. Justify your answer. [3]
Answer/Explanation
Ans:

Raman and Sanjay are members of a quiz team which has 9 members in total. Two photographs of the quiz team are to be taken.
For the first photograph, the 9 members will stand in a line.
(a) Question
How many different arrangements of the 9 members are possible in which Raman will be at the centre of the line?
Answer/Explanation
Ans:
[8! =] 40 320
(b) Question
How many different arrangements of the 9 members are possible in which Raman and Sanjay are not next to each other?
For the second photograph, the members will stand in two rows, with 5 in the back row and 4 in the front row.
Answer/Explanation
Ans:
Method 1 [^ ^ ^ R ^ ^ S ^ ^]
7! × 8C2 × 2
282 240
(c) Question
In how many different ways can the 9 members be divided into a group of 5 and a group of 4?
Answer/Explanation
Ans:
9C5 [× 4C4]
126
(d) Question
For a random division into a group of 5 and a group of 4, find the probability that Raman and Sanjay are in the same group as each other.
Answer/Explanation
Ans:
[Number of ways with Raman and Sanjay together on back row = ] 7C3
[Number of ways with Raman and Sanjay together on front row = ] 7C2
[Total =] 35 + 21
56
Probability = \(\frac{their 56}{their (c)} = \frac{56}{126}, \frac{4}{9}, 0.444\)
Question
A fair spinner with 5 sides numbered 1, 2, 3, 4, 5 is spun repeatedly. The score on each spin the number on the side on which the spinner lands.
(a) Find the probability that a score of 3 is obtained for the first time on the 8th spin.
(b) Find the probability that fewer than 6 spins are required to obtain a score of 3 for the first time.
Answer/Explanation
Ans:
a. (\frac{4}{5})^7\frac{1}{5}=]\frac{16384}{390625\) or 0.0419[43…]
b \(1.9\frac{4}{5})^5\) or \(\frac{1}{5}+\frac{4}{5}\times \frac{1}{5}(\frac{4}{5})^2\times \frac{1}{5}+(\frac{4}{5})^2\times \frac{1}{5}+(\frac{4}{5})^3\times \frac{1}{5}+(\frac{4}{5})^4\times \frac{1}{5}\)
\(\frac{2101}{3125}\) or 0.672[32]
Alternative method for question 1(b)
[P(at least 1 three scored in 5 throws)=]
$(\frac{1}{5})^5+^5C_4(\frac{1}{5})^4(\frac{4}{5})+^5C_3(\frac{1}{5})^3(\frac{4}{5})^2+^5C_2(\frac{1}{5})^2(\frac{4}{5})^3+^5C_4(\frac{1}{5}(\frac{4}{5})^4$
\(\frac{2101}{3125}\) or 0.672[32]
Question
Kayla is competing in a throwing event. A throw is counted as a success if the distance achieved is
greater than 30 metres. The probability that Kayla will achieve a success on any throw is 0.25.
(a) Find the probability that Kayla takes more than 6 throws to achieve a success. [2]
(b) Find the probability that, for a random sample of 10 throws, Kayla achieves at least 3 successes. [3]
Answer/Explanation
Ans
3 (b) 1 – P(0, 1, 2) = 1 – ( 0.7510C1 0.251 0.759+ 10C2 0.252 0.758 )
1 – (0·0563135 + 0·1877117 + 0·2815676)
0·474
Question
The score when two fair six-sided dice are thrown is the sum of the two numbers on the upper faces.
(a) Show that the probability that the score is 4 is \(\frac{1}{12}\) [1]
The two dice are thrown repeatedly until a score of 4 is obtained. The number of throws taken is
denoted by the random variable X.
(b) Find the mean of X. [1]
(c) Find the probability that a score of 4 is first obtained on the 6th throw. [1]
(d) Find P(X < 8). [2]
Answer/Explanation
Ans
1 (a) Prob of 4 (from 1,3, 3,1 or 2,2) \(=\frac{3}{36}=\frac{1}{12} \ AG\)
1 (b) \(Mean=\frac{1}{\frac{1}{12}}=12\)
1 (c) \(\left ( \frac{11}{12} \right )\times \frac{1}{12}=0.0539\ or \frac{161051}{2985984}\)
1 (d) \(1-\left ( \frac{11}{12} \right )^{7}\)
\(0.456\ or \ \frac{16344637}{35831808}\ )