Question
For her bedtime drink, Suki has either chocolate, tea or milk with probabilities 0.45, 0.35 and 0.2 respectively. When she has chocolate, the probability that she has a biscuit is 0.3. When she has tea, the probability that she has a biscuit is 0.6. When she has milk, she never has a biscuit.
Find the probability that Suki has tea given that she does not have a biscuit.
Answer/Explanation
Ans:
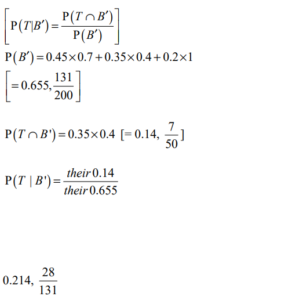
Question
Two ordinary fair dice, one red and the other blue, are thrown.
Event A is ‘the score on the red die is divisible by 3’.
Event B is ‘the sum of the two scores is at least 9’.
(a) Find P (A ∩ B). [2]
(b) Hence determine whether or not the events A and B are independent. [2]
Answer/Explanation
Ans
1 (a) 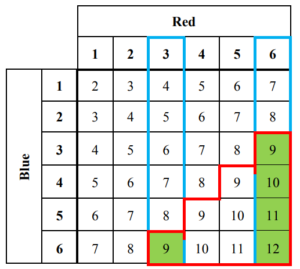
\(P(A\cap B )=\frac{5}{36}\)
1 (b) \(P(A)\times P(B)=\frac{1}{3}\times \frac{10}{36}\)
\(\frac{5}{54}\neq \frac{5}{36}\) so not independent
Alternative method for question 1(b)
P(B|A) = P(B)
\(P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{\frac{5}{36}}{\frac{1}{3}}\)
\(\frac{5}{12}\neq \frac{5}{18}\) so not independent
Question
In a certain town, 35% of the people take a holiday abroad and 65% take a holiday in their own country. Of those going abroad 80% go to the seaside, 15% go camping and 5% take a city break. Of those taking a holiday in their own country, 20% go to the seaside and the rest are divided equally between camping and a city break.
(i) A person is chosen at random. Given that the person chosen goes camping, find the probability that the person goes abroad. [5]
(ii) A group of n people is chosen randomly. The probability of all the people in the group taking a holiday in their own country is less than 0.002. Find the smallest possible value of n. [3]
Answer/Explanation
Ans:
