Question
A fair red spinner has edges numbered 1, 2, 2, 3. A fair blue spinner has edges numbered −3, −2, −1, −1.
Each spinner is spun once and the number on the edge on which each spinner lands is noted. The random variable X denotes the sum of the resulting two numbers.
(a) Draw up the probability distribution table for X.
(b)Given that E (X) = 0.25, find the value of Var (X).
Answer/Explanation
(a)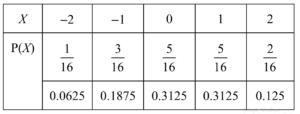
(b)$\begin{aligned} & \frac{1}{16} \times-2^2+\frac{3}{16} \times-1^2\left(+\frac{5}{16} \times 0^2\right)+\frac{5}{16} \times 1^2+\frac{2}{16} \times 2^2-\left(\frac{1}{4}\right)^2 \\ & \frac{1 \times 4+3 \times 1+5 \times 0+5 \times 1+2 \times 4}{16}-0.25^2\end{aligned}$
$\left[=\frac{5}{4}-\frac{1}{16}=\right] \frac{19}{16}, 1.1875$
Question
A company produces small boxes of sweets that contain 5 jellies and 3 chocolates. Jemeel chooses
3 sweets at random from a box.
(a) Draw up the probability distribution table for the number of jellies that Jemeel chooses. [4]
The company also produces large boxes of sweets. For any large box, the probability that it contains
more jellies than chocolates is 0.64. 10 large boxes are chosen at random.
(b) Find the probability that no more than 7 of these boxes contain more jellies than chocolates. [3]
Answer/Explanation
Ans
3 (a) 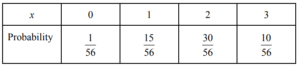
(B1 for probability distribution table with correct outcome values)
\(P(0)=\frac{3}{8}\times \frac{2}{7}\times \frac{1}{6}=\frac{1}{56}\)
\(P(1)=\frac{5}{8}\times \frac{3}{7}\times \frac{2}{6}\times 3=\frac{15}{56}\)
\(P(2)=\frac{5}{8}\times \frac{4}{7}\times \frac{3}{6}\times 3=\frac{30}{56}\)
\(P(3)=\frac{5}{8}\times \frac{4}{7}\times \frac{3}{6}=\frac{10}{56}\)
(M1 for denominator 8×7×6)
Any one probability correct (with correct outcome)
All probabilities correct
3 (b) \(1-P(8,9,10)=1-[^{10}C_{8}0.64^{8}0.36^{2}+^{10}C_{9}0.64^{9}0.36^{1}+0.64^{10}]\)
1 – (0.164156 + 0.064852 + 0.11529)
0.759
Question
A flower shop has 5 yellow roses, 3 red roses and 2 white roses. Martin chooses 3 roses at random. Draw up the probability distribution table for the number of white roses Martin chooses. [4]
Answer/Explanation
Ans:
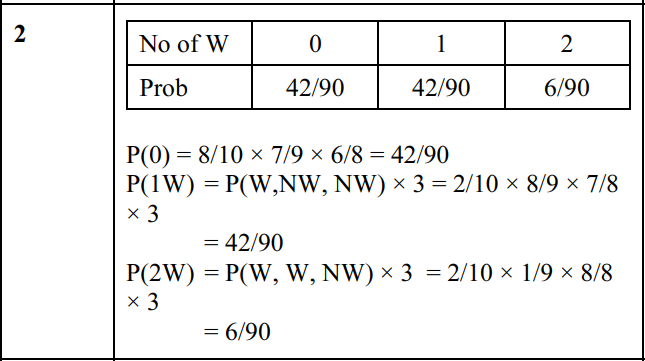
Question
An ordinary fair die is thrown repeatedly until a 1 or a 6 is obtained.
(a) Find the probability that it takes at least 3 throws but no more than 5 throws to obtain a 1 or 6.
On another occasion, this die is thrown 3 times. The random variable X is the number of times that a 1 or a 6 is obtained.
(b) Draw up the probability distribution table for X.
(c) Find E(X).
Answer/Explanation
Ans:
(a) \((\frac{1}{3})(\frac{2}{3})^2+(\frac{1}{3})(\frac{2}{3})^3+(\frac{1}{3})(\frac{2}{3})^4\)
\(=\frac{4}{27}+\frac{8}{81}+\frac{16}{243}(=\frac{2432}{7776})\)
\(=\frac{76}{243}\) or 0.313
(b)
| x | 0 | 1 | 2 | 3 |
| P(x) | \(\frac{8}{27}\) | \(\frac{12}{27}\) | \(\frac{6}{27}\) | \(\frac{1}{27}\) |
P(0) = \((\frac{2}{3})^3\)
P(1) = \((\frac{1}{3})(\frac{2}{3})^2 \times 3\)
P(2) = \((\frac{2}{3})(\frac{1}{3})^2 \times 3 \)
P(3) = \((\frac{1}{3})^3\)
(c) \(E(X)=[0 \times \frac{8}{27}]+1 \times \frac{12}{27} + 2 \times \frac{6}{27} + 3 \times \frac{1}{27}\)
\(=[\frac{0}{27}]+\frac{12}{27}+\frac{12}{27}+\frac{3}{27}\)
= 1
Question
Georgie has a red scarf, a blue scarf and a yellow scarf. Each day she wears exactly one of these
scarves. The probabilities for the three colours are 0.2, 0.45 and 0.35 respectively. When she wears a
red scarf, she always wears a hat. When she wears a blue scarf, she wears a hat with probability 0.4.
When she wears a yellow scarf, she wears a hat with probability 0.3.
(a) Find the probability that on a randomly chosen day Georgie wears a hat.
(b) Find the probability that on a randomly chosen day Georgie wears a yellow scarf given that she does not wear a hat.
Answer/Explanation
Ans:
- \(0.2[\times1]+0.45\times0.35\times0.3\)
0.485 or \(\frac{97}{200}\) - \((Y|\bar{H})=\frac{P(Y\cap \bar{H})}{P(\bar{H})}=\frac{0.35\times 0.7}{1-their(a)}=\frac{0.245}{0.515}\)
0.476 or \(\frac{49}{103}\)
Two fair coins are thrown at the same time. The random variable X is the number of throws of the two coins required to obtain two tails at the same time.
(a) Question
Find the probability that two tails are obtained for the first time on the 7th throw.
Answer/Explanation
Ans:
\(\left ( \frac{3}{4} \right )^{6} \frac{1}{4}\)
\(0.0445,\frac{729}{16384}\)
(b) Question
Find the probability that it takes more than 9 throws to obtain two tails for the first time.
Answer/Explanation
Ans:
\(\left ( \frac{3}{4} \right )^{9}\)
\(0.0751,\frac{19683}{262144}\)
A fair spinner has edges numbered 0, 1, 2, 2. Another fair spinner has edges numbered −1, 0, 1. Each spinner is spun. The number on the edge on which a spinner comes to rest is noted. The random variable X is the sum of the numbers for the two spinners.
(a) Question
Draw up the probability distribution table for X.
Answer/Explanation
Ans:

(b) Question
Find Var (x).
Answer/Explanation
Ans:
\(E (X) = -\frac{1}{12}+\frac{4}{12}+\frac{6}{12}+\frac{6}{12} \left [ =\frac{15}{12} \right ]\)
\(Var (X) = \frac{1}{12}+0 + \frac{4}{12}+\frac{12}{12}+\frac{18}{12}-\left ( \frac{15}{12} \right )^{2}\)
\(\left [ \frac{35}{12} – \frac{25}{16} =\right ] \frac{65}{48}, 1.35\)
Question
There are 400 students at a school in a certain country. Each student was asked whether they preferred
swimming, cycling or running and the results are given in the following table.
| Swimming | Cycling | Running | |
| Female | 104 | 50 | 66 |
| Male | 31 | 57 | 92 |
A student is chosen at random.
(a) (i) Find the probability that the student prefers swimming.
(ii) Determine whether the events ‘the student is male’ and ‘the student prefers swimming’ are independent, justifying your answer.
On average at all the schools in this country 30% of the students do not like any sports.
(b) (i) 10 of the students do not like any sports.
Find the probability that at least 3 of these students do not like any sports.
(ii) 90 students from this country are now chosen at random.
Use an approximation to find the probability that fewer than 32 of them do not like any sports.
Answer/Explanation
Ans:
- (i) \([\frac{104+31}{400}=]\frac{135}{400},\frac{27}{80},0.3375\)
(ii) Method 1
\(P(M)=\frac{180}{400},0.45 P(S)=\frac{135}{400},0.3375 P(M\cap S)=\frac{31}{400},0.0775\)
\(\frac{180}{400}\times \frac{135}{400}=\frac{243}{1600},0.151875≠\frac{31}{400}\) so NOT independent
Method 2
\(P(M\cap S)=\frac{31}{400} P(S)=\frac{135}{400} P(M)=\frac{180}{400}\)
\(P(M|S)=\frac{\frac{31}{400}}{\frac{135}{400}}=\frac{31}{135},0.2296… ≠\frac{180}{400}\) so NOT independent - (i) Method 1 [1-P(0, 1, 2)]
\(=1-(^{10}C_00.3^00.7^{10}+^{10}C_10.3^10.7^9+^10C_20.3^20.7^8)\)
=1-(0.028248+0.131061+0.233474)
Method 2 [P(3, 4, 5,6,7,8,9,10)=]
\(^{10}C_30.3^30.7^7+^{10}C_40.3^40.7^6+^{10}C_50.3^50.7^5+^{10}C_60.3^60.7^4+^{10}C_70.3^70.7^3+^{10}C_80.3^80.7^2+^{10}C_90.3^90.7^1+^{10}C_{10}0.3^{10}0.7^0\)
=0.617
[p=0.3]
Mean \(= 0.3 \times 90=27;\)
variance \(=0.3 \times 90 \times 0.7 = 18.9\)
\(P(X<32)=P(z<\frac{31.5-27}{\sqrt{18.9}})\)
=Φ(1.035)
=0.850
Question
The random variable X takes each of the values 1, 2, 3, 4 with probability ¼. Two independent values
of X are chosen at random. If the two values of X are the same, the random variable Y takes that
value. Otherwise, the value of Y is the larger value of X minus the smaller value of X.
(a) Draw up the probability distribution table for Y. [4]
(b) Find the probability that Y = 2 given that Y is even. [2]
Answer/Explanation
Ans
4 (a) 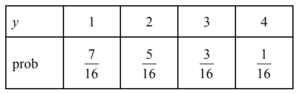
4 (b) \(P(2|even)=\frac{\frac{5}{16}}{\frac{6}{16}}\)
\(\frac{5}{6}\) or 0·833