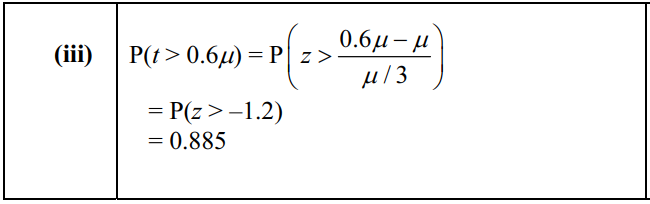Question
The probability that a student at a large music college plays in the band is 0.6. For a student who plays
in the band, the probability that she also sings in the choir is 0.3. For a student who does not play
in the band, the probability that she sings in the choir is x. The probability that a randomly chosen
student from the college does not sing in the choir is 0.58.
(a) Find the value of x. [3]
Two students from the college are chosen at random.
(b) Find the probability that both students play in the band and both sing in the choir. [2]
Answer/Explanation
Ans
2 (a) 0·6 × 0·7 + 0·4(1 – x) = 0·58
≡ 0·42 + 0·4(1 – x) = 0·58
x = 0·6
Alternative method for question 2(a)
0·6 × 0·3 + 0·4x = 0·42
≡ 0·18 + 0·4 x = 0·42
x = 0·6
2 (b) ( 0.6 × 0.3)2
0.0324
3 (a) \(P(x\gt 6)=0.75^{6}\)
\(0.178,\frac{729}{4096}\)
Question
The lengths of female snakes of a particular species are normally distributed with mean 54 cm and
standard deviation 6.1 cm.
(a) Find the probability that a randomly chosen female snake of this species has length between
50 cm and 60 cm. [4]
The lengths of male snakes of this species also have a normal distribution. A scientist measures the
lengths of a random sample of 200 male snakes of this species. He finds that 32 have lengths less than
45 cm and 17 have lengths more than 56 cm.
(b) Find estimates for the mean and standard deviation of the lengths of male snakes of this species. [5]
Answer/Explanation
Ans
6 (a) \(P\left ( \frac{50-54}{6.1}< z< \frac{60-54}{6.1} \right )=P(-0.6557< Z< 0.9836)\)
Both values correct
Φ (0.9836) – Φ (–0.6557) = Φ (0.9836) + Φ (0.6557) – 1
= 0.8375 + 0.7441 – 1
(Correct area)
0.582
6 (b) \(\frac{45-\mu }{\sigma }=-0.994\)
\(\frac{56-\mu }{\sigma }=-1.372\)
One appropriate standardisation equation with µ, σ ,z-value (not probability) and 45 or 56.
11 = 2.366σ
(M1 for correct algebraic elimination of µ or σ from their two simultaneous equations to form an equation in one variable)
σ = 4.65, μ = 49.6
Question
The times taken by a garage to fit a tow bar onto a car have a normal distribution with mean m hours and standard deviation 0.35 hours. It is found that 95% of times taken are longer than 0.9 hours.
(i) Find the value of m. [3]
(ii) On one day 4 cars have a tow bar fitted. Find the probability that none of them takes more than 2 hours to fit. [5]
The times in hours taken by another garage to fit a tow bar onto a car have the distribution \(N\left ( \mu ,\sigma ^{2} \right )\) where \(\mu =3\sigma \) .
(iii) Find the probability that it takes more than 0.6- hours to fit a tow bar onto a randomly chosen car at this garage. [3]
Answer/Explanation
Ans: