Question
(a)
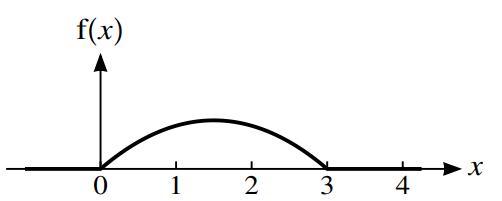
The diagram shows the graph of the probability density function, f, of a random variable X, where
\(f\left ( x \right )= \left\{\begin{matrix}\frac{2}{9}\left ( 3x-x^{2} \right )\\ 0\end{matrix}\right.\)
\(0\leqslant x\leqslant 3,\)
otherwise.
(i) State the value of E(X) and find Var(X).[4]
(ii) State the value of \(P\left ( 1.50\leqslant x\leqslant 4\right )\). [1]
(iii) Given that \(P\left ( 1\leqslant x\leqslant 2\right )= \frac{13}{27},\) find \(P\left ( X> 2 \right )\) .[4]
(b) A random variable, W, has probability density function given by
\(g\left ( w \right )= \left\{\begin{matrix}aw\\ 0\end{matrix}\right.\)
\(0\leqslant w\leqslant b,\)
otherwise,
where a and b are constants. Given that the median of W is 2, find a and b.[4]
Answer/Explanation
Ans:
