Question
The equation of a curve is \(y=x^{3}+px^{2}\) ,where p is a positive constant .
(i)Show that the origin is a stationary point on the curve and find the coordinates of the other stationary point in terms of p.
(ii)Find the nature of each of the stationary points.
Another curve has equation \(y=x^{3}+px^{2}+px\)
(iii)Find the set of values of p for which this curve has n o stationary points.
▶️Answer/Explanation
(i) To determine whether the origin is a stationary point on the curve \(y = x^3 + px^2\), we need to find the first and second derivatives of the curve and then evaluate them at \(x = 0\).
The first derivative of \(y\) with respect to \(x\) is:
\(y’ = 3x^2 + 2px\)
\(y'(0) = 3(0)^2 + 2p(0) = 0\)
Since \(y'(0) = 0\), this indicates that the origin (\(x = 0\)) is a stationary point on the curve.
To find the coordinates of the other stationary point, we need to find the value of \(x\) where \(y’\) is also equal to zero:
\(0 = 3x^2 + 2px\)
\(0 = x(3x + 2p)\)
\(x = 0\) (which corresponds to the origin, where we already know there is a stationary point).
\(3x + 2p = 0\)
To find the value of \(x\) for the second stationary point, solve for \(x\) in the second equation:
\(3x + 2p = 0\)
\(3x = -2p\)
\(x = -\frac{2p}{3}\)
So, the other stationary point has coordinates \(\left(-\frac{2p}{3}, f\left(-\frac{2p}{3}\right)\right)\).
(ii) To determine the nature of each of the stationary points, we can use the second derivative test. We need to find the second derivative \(y”\) and evaluate it at both \(x = 0\) and \(x = -\frac{2p}{3}\).
The second derivative of \(y\) is:
\(y” = 6x + 2p\)
Evaluate \(y”\) at \(x = 0\):
\(y”(0) = 6(0) + 2p = 2p\)
Since \(y”(0) = 2p\), and \(p\) is positive (given that \(p\) is a positive constant), this indicates that the stationary point at the origin is a local minimum.
Now, evaluate \(y”\) at \(x = -\frac{2p}{3}\):
\(y”\left(-\frac{2p}{3}\right) = 6\left(-\frac{2p}{3}\right) + 2p = -4p + 2p = -2p\)
Since \(y”\left(-\frac{2p}{3}\right) = -2p\), and \(p\) is positive, this indicates that the other stationary point at \(\left(-\frac{2p}{3}, f\left(-\frac{2p}{3}\right)\right) = \left(-\frac{2p}{3}, -\frac{4p^3}{27}\right)\) is also a local minimum.
(iii) For the curve \(y = x^3 + px^2 + px\), to find the set of values of \(p\) for which this curve has no stationary points,
\(y’ = 3x^2 + 2px + p\)
For a stationary point, we need \(y’\) to be equal to zero:
\(0 = 3x^2 + 2px + p\)
The discriminant \(\Delta\) is given by:
\(\Delta = (2p)^2 – 4(3)(p)\)
\(\Delta = 4p^2 – 12p = 4p(p – 3)\)
To have no stationary points, we need \(\Delta\) to be negative because it means that the quadratic equation has no real solutions.
\( \therefore \) \(4p(p – 3) < 0\)
\(\rightarrow 0< p< 3\)
Question
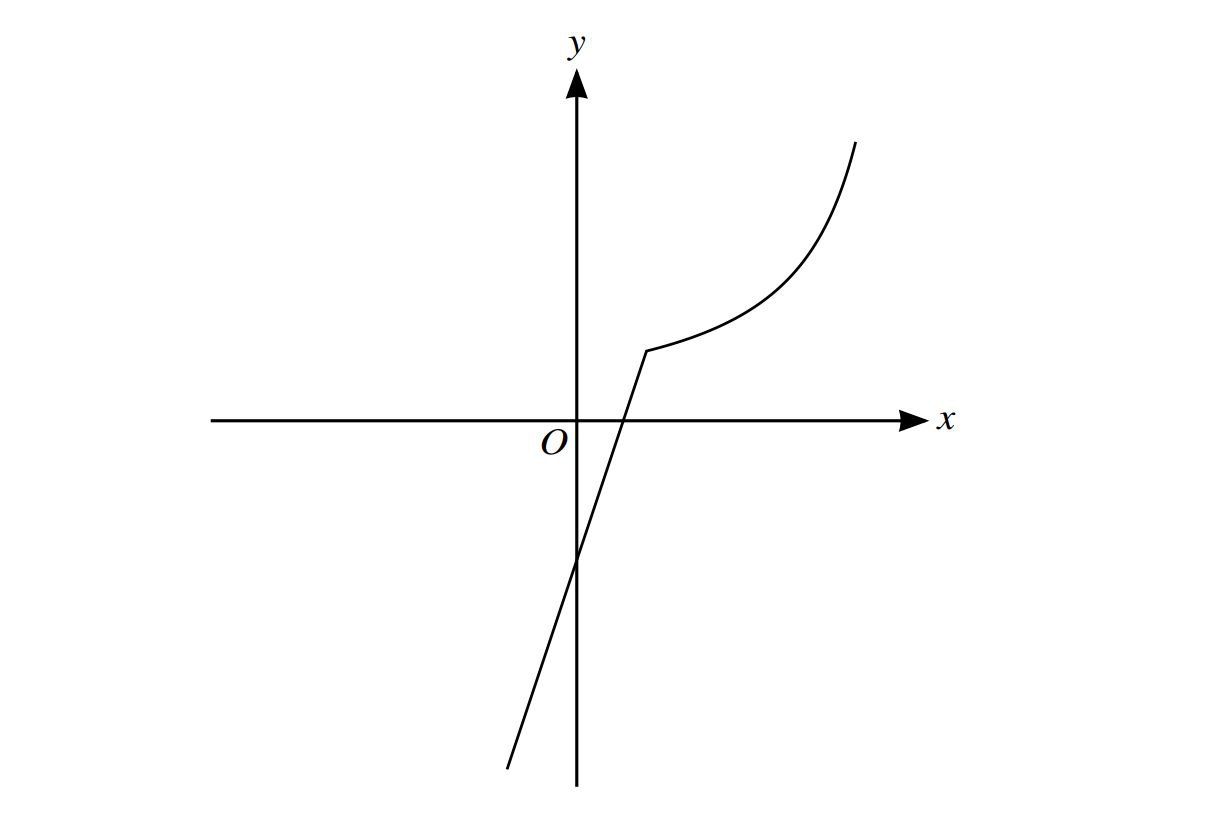
The diagram shows that the function $\mathrm{f}$ defined for $-1 \leq x \leq 4$, where
$$
f(x)= \begin{cases}3 x-2 & \text { for }-1 \leqslant x \leqslant 1 \\ \frac{4}{5-x} & \text { for } 1<x \leqslant 4\end{cases}
$$
(i)State the range of $f$.
(ii)Copy the diagram and on your copy sketch the graph of $y=f^{-1}(x)$
(iii)Obtain expressions to define the function $f^{-1}$,giving also the set of values for which each expression is valid.
▶️Answer/Explanation
(i) The range of a function represents the set of all possible values that the function can take on for its given domain. In the case of the function \(f(x)\), it is defined for the domain \(-1 \leq x \leq 4\), and it consists of two distinct pieces:
\(\Rightarrow\) For the interval \(-1 \leq x \leq 1\), the function is defined as \(f(x) = 3x – 2\). In this interval, as \(x\) varies from -1 to 1, the function \(f(x)\ varies from \(3(-1) – 2 = -5\) to \(3(1) – 2 = 1\). So, for this part of the domain, the range of \(f(x)\ is \(-5 \leq f(x) \leq 1\).
\(\Rightarrow \) For the interval \(1 < x \leq 4\), the function is defined as \(f(x) = \frac{4}{5-x}\). In this interval, as \(x\) varies from 1 to 4, the function \(f(x)\ takes on values that change continuously.
\(\lim_{x \to 5^-} f(x) = \lim_{x \to 5^-} \frac{4}{5-x} = +\infty\)
As \(x\) approaches 5 from the left, \(f(x)\ becomes unbounded and approaches positive infinity. This means that for \(x\) values close to, but less than 5, \(f(x)\ can take on arbitrarily large positive values. However, it never reaches 5 because that would make the denominator zero. So, for this part of the domain, the range of \(f(x)\ is \(-\infty < f(x) < +\infty\), but \(f(x)\ never equals 5.
Combining both ranges, the overall range of the function \(f(x\) is \(-5 \leq f(x) \leq 1\) for the given domain \(-1 \leq x \leq 4\), and the function takes all real values within this range except for the value 5, which is excluded in the second piece due to the asymptote at \(x = 5\).
The range is given as \(-5 \leq f(x) \leq 4\) for both \(x\) and \(y\).
(ii) To sketch the graph of \(y = f^{-1}(x)\), you can follow these steps:
1. Reflect the graph of \(y = f(x)\) in the line \(y = x\). This means that for each point \((a, b)\) on the graph of \(y = f(x)\, you plot a corresponding point \((b, a)\ on the graph of \(y = f^{-1}(x)\.
2. Determine the domain of \(f^{-1}(x)\ based on the reflection. Since the original function \(f(x)\ was defined for \(-1 \leq x \leq 4\), the range of \(f(x)\ will become the domain of \(f^{-1}(x)\ after reflection.
3. Plot the points and sketch the curve for \(y = f^{-1}(x)\ within its valid domain.
\(f^{-1}\left ( x \right )\) approximately correct (independent of f)
Closed region between (1,1)and (4,4) line reaches x-axis.
(iii) To obtain expressions that define the function \(f^{-1}(x)\, we need to find the inverse of each piece of the function \(f(x)\.
For the first piece, \(f(x) = 3x – 2\ for \(-1 \leq x \leq 1\, to find the inverse, swap \(x\ and \(y\ and solve for \(y\:
\(x = 3y – 2\)
\(3y = x + 2\)
\(y = \frac{x + 2}{3\)
So, the inverse function for this piece is \(f^{-1}(x) = \frac{x + 2}{3\ for \(-1 \leq x \leq 1\.
For the second piece, \(f(x) = \frac{4}{5-x\ for \(1 < x \leq 4\, to find the inverse, swap \(x\ and \(y\ and solve for \(y\:
\(x = \frac{4}{5-y\)
\(\frac{4}{5-y} = x\)
\(5-y = \frac{4}{x\)
\(-y = \frac{4}{x} – 5\)
\(y = 5 – \frac{4}{x\)
So, the inverse function for this piece is \(f^{-1}(x) = 5 – \frac{4}{x\ for \(1 < x \leq 4\.\)
Question
The function \( f:x\rightarrow x^{2}-4x+k\) is defined for the domain \(x\geq p\) ,where k and p are constants.
(i)Express \(f\left ( x \right )\) in the form ,\(\left ( x+a \right )^{2}+b+k\) where a and b are constants.
(ii)State the range of f in terms of k.
(iii)State the smallest value of p for which f is one-one.
(iv)For the value of p found in part (iii),find an expression for \(f^{-1}\left ( x \right )\) and state the domain of \(f^{-1}\) giving your answer in terms of k.
▶️Answer/Explanation
(i) To express the function \(f(x)\) in the form \((x+a)^2+b+k\), you need to complete the square. Here’s how you can do it:
\(f(x) = x^2 – 4x + k\)
\(f(x) = (x^2 – 4x + 4) + k – 4\)
\(f(x) = (x – 2)^2 + (k – 4)\)
So, \(a = -2\) and \(b = k – 4\).
(ii) The range of the function \(f(x)\) in terms of \(k\) can be determined from the expression \((x – 2)^2 + (k – 4)\). The minimum value of \((x – 2)^2\) is \(0\), and it can take any non-negative value. So, the range of \(f(x)\) is \((k – 4, +\infty)\) in terms of \(k\).
(iii) To make \(f(x)\) one-one (injective), the function must be strictly increasing or decreasing. For \(f(x) = x^2 – 4x + k\), it’s a quadratic function, and its behavior depends on the coefficient of the \(x^2\) term (which is 1 in this case). A quadratic function is strictly increasing if the coefficient of \(x^2\) is positive. So, for \(f(x)\) to be one-one, \(1 > 0\), which implies that \(p\) must be greater than 2.
(iv) To find the expression for \(f^{-1}(x)\) and state its domain, we first need to interchange the roles of \(x\) and \(y\):
\(x-2=\left ( \pm \right )\sqrt{y+4-k}\)
\(x=2+\sqrt{y+4-k}\)
\(f^{-1}\left ( x \right )=2+\sqrt{x+4-k}\)
Domain is \(x> k-4\) or \(\left [ k-4,\infty \right ]\)
or \(\left ( k-4,\infty \right )\)