Question
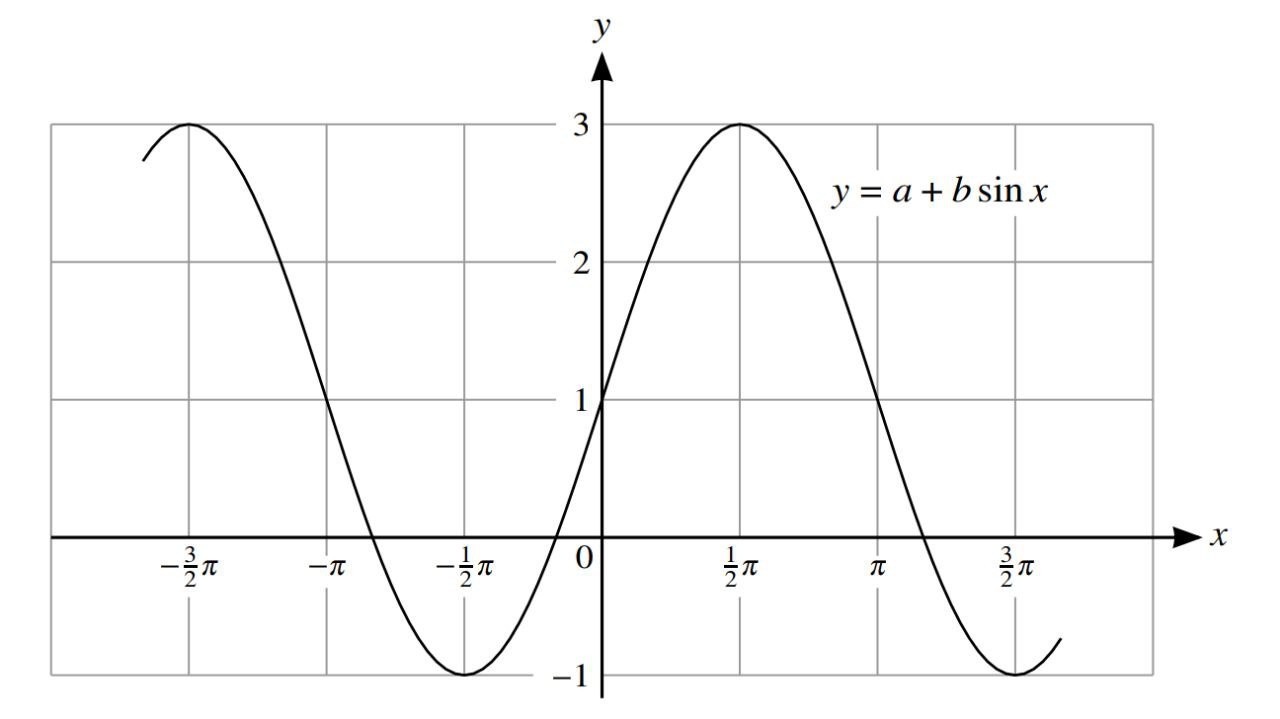
The diagram shows part of the graph of \(y=a+b\sin x\). State the values of the constants a and b.
▶️Answer/Explanation
In this case, the graph is shifted upward by 1 unit.The constant a=1 represents a vertical shift of the graph.The amplitude is the half-range of the oscillation, which is 2 in this case.The constant b=2 represents the amplitude of the sine function. So, the equation y=1+2sinx describes a sine function with an amplitude of 2, centered at y=1.
Question
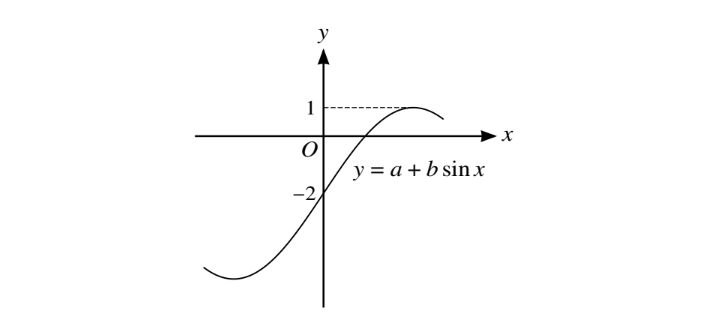
(a)The diagram shows part of the graph of \(y=a+b\sin x\).Find the values of constant a and b.
(b)(i)Show that the equation \(\left ( \sin \Theta +2\cos \Theta \right )\left ( 1+\sin \Theta -\cos \Theta \right )=\sin \Theta \left ( 1+\cos \Theta \right )\)
may be expressed as \(3\cos ^{2}\Theta -2\cos \Theta -1=0\).
(iii)Hence solve the equation \(\left ( \sin \Theta +2\cos \Theta \right )\left ( 1+\sin \Theta-\cos \Theta \right )=\sin \Theta \left ( 1+\cos \Theta \right )\) for \(-180^{\circ}\leq \Theta \leq 180^{\circ}\)
▶️Answer/Explanation
(a) The equation of the graph is \(y = -2 + 3 \sin x\).
Here’s what these values mean for the graph:
The constant \(a = -2\) represents a vertical shift of the graph. In this case, the graph is shifted downward by 2 units.
The constant \(b = 3\) represents the amplitude of the sine function. The amplitude is the half-range of the oscillation, which is 3 in this case. This means the graph oscillates between \(-2 + 3 = 1\) and \(-2 – 3 = -5\).
So, the equation \(y = -2 + 3 \sin x\) describes a sine function with an amplitude of 3, centered at \(y = -2\).
(b)(i) Let’s simplify the given equation:
\(
\begin{align*}
& (\sin \Theta + 2 \cos \Theta)(1 + \sin \Theta – \cos \Theta) = \sin \Theta(1 + \cos \Theta) \\
& (\sin \Theta + 2 \cos \Theta)(1 + \sin \Theta – \cos \Theta) – \sin \Theta(1 + \cos \Theta) = 0 \\
& \sin \Theta + 2 \cos \Theta + \sin^2 \Theta – \cos^2 \Theta + 2 \sin \Theta \cos \Theta – \sin \Theta – \cos \Theta = 0 \\
& \sin^2 \Theta – \cos^2 \Theta + 2 \sin \Theta \cos \Theta = 0 \\
& (\sin \Theta + \cos \Theta)(\sin \Theta – \cos \Theta) + 2 \sin \Theta \cos \Theta = 0 \\
& \sin \Theta + \cos \Theta + 2 \sin \Theta \cos \Theta – \sin \Theta \cos \Theta = 0 \\
& \sin \Theta + \cos \Theta + \sin \Theta \cos \Theta = 0 \\
& \cos \Theta(1 + \sin \Theta) + \sin \Theta \cos \Theta = 0 \\
& \cos \Theta(1 + \sin \Theta + \sin \Theta) = 0 \\
& \cos \Theta(1 + 2 \sin \Theta) = 0.
\end{align*}
\)
Now, we know that \(\cos \Theta\) cannot be zero for all values of \(\Theta\), so we divide both sides by \(\cos \Theta\):
\( 1 + 2 \sin \Theta = 0 \)
\( 2 \sin \Theta = -1 \)
\( \sin \Theta = -\frac{1}{2} \)
\( \sin^2 \Theta = \frac{1}{4} \)
Using the identity \(\sin^2 \Theta + \cos^2 \Theta = 1\):
\( \cos^2 \Theta = 1 – \frac{1}{4} \)
\( \cos^2 \Theta = \frac{3}{4} \)
\( 3 \cos^2 \Theta – 2 \cos \Theta – 1 = 0 \)
(ii)\( 3 \cos^2 \Theta – 2 \cos \Theta – 1 = 0 \)
\(3\cos ^{2}\Theta -3\cos \Theta +\cos \Theta -1=0\)
\(3\cos \Theta (\cos \Theta -1)+1(\cos \Theta -1)=0\)
\( (3\cos \Theta +1)(\cos \Theta -1)=0 \)
\(\cos \Theta =-\frac{1}{3} \) or \( \cos \Theta =1\)
If \(\cos \Theta = 1\), then \(\Theta = \cos^{-1}(1)\). However, the inverse cosine of 1 is \(0^\circ\).
If \(\cos \Theta = -\frac{1}{3}\), then \(\Theta = \cos^{-1}\left(-\frac{1}{3}\right)\). This value is approximately \(109.5^\circ\) or \(-109.5^\circ\) because the cosine function is negative in the second and third quadrants.
So,
\(\cos \Theta = 1\) implies \(\Theta = 0^\circ\).
\(\cos \Theta = -\frac{1}{3}\) implies \(\Theta \approx 109.5^\circ\) or \(-109.5^\circ\).
Question
The function f is defined by \(f: x\rightarrow 4 sin x – 1\) for \(\frac{-\Pi}{2}\leq x\leq\frac{\Pi}{2}\).
(i) State the range of f.
(ii) Find the coordinates of the points at which the curve y = f(x) intersects the coordinate axes.
(iii) Sketch the graph of y = f(x).
(iv) Obtain an expression for \(f^{-1}(x)\) , stating both the domain and range of \(f^{-1}\).
▶️Answer/Explanation
(i) State the range of \(f\):
The function \(f(x) = 4 \sin x – 1\) is a sine function with an amplitude of 4 and a vertical shift downward by 1 unit. The range of a sine function is \([-1, 1]\), so when you multiply it by 4 and shift it downward by 1, the range becomes \([-5, 3]\).
So, the range of \(f\) is \([-5, 3]\).
(ii) Find the coordinates of the points at which the curve \(y = f(x)\) intersects the coordinate axes:
For the \(y\)-axis, where \(x = 0\), \(f(0) = 4 \sin 0 – 1 = -1\). So, the point of intersection is \((0, -1)\).
For the \(x\)-axis, where \(y = 0\), solve \(4 \sin x – 1 = 0\) for \(x\):
\( 4 \sin x = 1 \)
\( \sin x = \frac{1}{4} \)
Taking the arcsine (or inverse sine) of both sides:
\( x = \sin^{-1}\left(\frac{1}{4}\right) \)
\( x \approx 0.253 \text{ radians} \)
So, the point of intersection with the \(x\)-axis is approximately \((0.253, 0)\).
The correct coordinates are:
For the \(y\)-axis: \((0, -1)\)
For the \(x\)-axis: \((0.253, 0)\)
(iii) 
The function \(f(x) = 4 \sin x – 1\) is a sine function with an amplitude of 4, centered at \(x = 0\), and shifted downward by 1 unit. The graph oscillates between \(-5\) and \(3\).
(iv) Obtain an expression for \(f^{-1}(x)\), stating both the domain and range of \(f^{-1}\):
To find \(f^{-1}(x)\), interchange \(x\) and \(y\) and solve for \(y\):
\( x = 4 \sin y – 1 \)
\( 4 \sin y = x + 1 \)
\( \sin y = \frac{x + 1}{4} \]
\( y = \sin^{-1}\left(\frac{x + 1}{4}\right) \)
The domain of \(f^{-1}(x)\) is determined by the domain of \(f(x)\), which is \(\frac{-\pi}{2} \leq x \leq \frac{\pi}{2}\). The range of \(f^{-1}(x)\) is determined by the range of \(f(x)\), which is \([-5, 3]\).
So, the expression for \(f^{-1}(x)\) is:
\( f^{-1}(x) = \sin^{-1}\left(\frac{x + 1}{4}\right) \)
with the domain \(\frac{-\pi}{2} \leq x \leq \frac{\pi}{2}\) and the range \([-5, 3]\).