Question
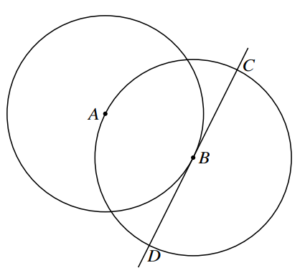
The diagram shows a circle with centre A passing through the point B. A second circle has centre B
and passes through A. The tangent at B to the first circle intersects the second circle at C and D.
The coordinates of A are (−1, 4) and the coordinates of B are (3, 2).
(a) Find the equation of the tangent CBD.
(b) Find an equation of the circle with centre B.
(c) Find, by calculation, the x-coordinates of C and D.
▶️Answer/Explanation
(a) Equation of the Tangent \(CBD\):
the slope of \(AB\):\( m_{AB} = \frac{4-2}{-1-3} = -\frac{1}{2} \)
Now,tangent CBD is perpendicular to AB,hence slope of tangent CBD is 2.
The point-slope form of the equation for the tangent line is given by:
\( y – y_1 = m_{AB}(x – x_1) \)
Substitute the coordinates of point \(B\) into the equation:
\( y – 2 =2(x – 3) \)
Equation of the Tangent CBD:\( y – 2 =2(x – 3) \)
(b) Equation of the Circle with Center B:
\begin{aligned}
& A B=\sqrt{(3-(-1))^2+(2-4)^2} \\
& A B=\sqrt{4^2+(-2)^2} \\
& A B=\sqrt{16+4} \\
& A B=\sqrt{20} \\
& A B=2 \sqrt{5}
\end{aligned}
\(AB=r =\sqrt{20}\)
The equation of the circle with center \(B\) is:
\( (x – 3)^2 + (y – 2)^2 = 20 \)
Equation of the Circle with Center B:\( (x – 3)^2 + (y – 2)^2 = 20 \)
(c) \(x\)-Coordinates of \(C\) and \(D\):
The equation by substituting the equation of the circle into the equation of the tangent:
\( (x – 3)^2 + (2x – 6)^2 = 20 \)
Then,
\( 5x^2 – 30x + 25 = 0 \)
\( (5)(x-5)(x-1) = 0 \)
\( x = 5, 1 \)
So, the \(x\)-coordinates of points \(C\) and \(D\) are \(x = 5\) and \(x = 1\), respectively.
Question
The points A(7, 1), B(7, 9) and C(1, 9) are on the circumference of a circle.
(a) Find an equation of the circle.
(b) Find an equation for the tangent to the circle at B.
▶️Answer/Explanation
(a) Given three points \(A(7,1)\), \(B(7,9)\), and \(C(1,9)\) on the circumference of the circle, we can use the fact that the center of the circle is equidistant from these points.
The center of the circle \((h, k)\) is the midpoint of the line segment connecting any two points on the circumference. Let’s use \(A\) and \(C\) to find the center:
\( h = \frac{7 + 1}{2} = 4 )
\( k = \frac{1 + 9}{2} = 5 \)
So, the center of the circle is \((4, 5)\).
Now, we need to find the radius (\(r\)), which is the distance from the center to any of the given points (let’s use \(A\)):
\( r = \sqrt{(7 – 4)^2 + (1 – 5)^2} = \sqrt{(3)^{2}+(-4)^2} = 5 \)
\( (x – 4)^2 + (y – 5)^2 = 5^2 \)
\( (x – 4)^2 + (y – 5)^2 = 25 \)
(b) The gradient of the radius from the center of the circle to point \(B(7, 9)\) is calculated as:
\( \text{Gradient of radius} = \frac{y_B – y_C}{x_B – x_C} = \frac{9 – 5}{7 – 4} = \frac{4}{3} \)
Now, for the equation of the tangent, we can use the fact that the radius and the tangent at the point of contact are perpendicular. Therefore, the negative reciprocal of the gradient of the radius is the gradient of the tangent.
\( \text{Gradient of tangent} = -\frac{1}{\text{Gradient of radius}} = -\frac{1}{\frac{4}{3}} = -\frac{3}{4} \)
Now, using the point-slope form of a line (\(y – y_1 = m(x – x_1)\)),
where \((x_1, y_1)\) is a point on the line and \(m\) is the gradient,
The equation of the tangent at \(B(7, 9)\):
\( y – 9 = -\frac{3}{4}(x – 7) \)
\( y – 9 = -\frac{3}{4}(x – 7) \)
Question
A circle with centre (5, 2) passes through the point (7, 5).
(a) Find an equation of the circle.
The line y = 5x − 10 intersects the circle at A and B.
(b) Find the exact length of the chord AB.
▶️Answer/Explanation
(a) Equation of the Circle:
The general equation of a circle with center \((h, k)\) and radius \(r\) is given by:
\( (x – h)^2 + (y – k)^2 = r^2 \)
Given the center \((h, k) = (5, 2)\) and a point on the circle \((x_1, y_1) = (7, 5)\), we can find the radius (\(r\)) using the distance formula:
\( r = \sqrt{(x_1 – h)^2 + (y_1 – k)^2} \)
\( r = \sqrt{(7 – 5)^2 + (5 – 2)^2} \)
\( r = \sqrt{2^2 + 3^2} \)
\( r = \sqrt{13} \)
\( (x – 5)^2 + (y – 2)^2 = (\sqrt{13})^2 \)
\( (x – 5)^2 + (y – 2)^2 = 13 \)
So, the equation of the circle is \( (x – 5)^2 + (y – 2)^2 = 13 \).
(b) Length of Chord AB:
The equation of the line \(\mathrm{y} = 5\mathrm{x} – 10\) intersects the circle at points \(A\) and \(B\). To find the points of intersection, substitute the equation of the line into the equation of the circle and solve for \(x\).
\( (x – 5)^2 + (5x – 12)^2 = 13 \)
\(26x^{2}-130x+156=0\)
\(26(x-2)(x-3)=0\)
Hence,coordinates are (2,0) and (3,5).
The distance formula to find the length of chord AB:
\(AB^{2}=(3-2)^{2}+(5-0)^{2}\)
\(AB^{2}=1+25\)
\(AB^{2}=26\)
\(AB=\sqrt{26}\)