Question
A curve has equation \(y=x^{2}-4x+4 \) and a line has equation y=mx ,where m is a constant.
(i)For the case where m=1,the curve and the line intersect at the points A and B.Find the coordinates of mid-point of AB.
(ii)Find the non-zero value of m for which the line is a tangent to the curve ,and find the coordinates of the point where the tangent touches the curve.
▶️Answer/Explanation
(i)\(x^{2}-4x+4=x\Rightarrow x^{2}-5x+4=0\)
\(\left ( x-1 \right )\left ( x-4 \right )=0\)
So, the points of intersection A and B are (4,4).
By using midpoint formula,\( M\left(\frac{x_A+x_B}{2}, \frac{y_A+y_B}{2}\right)\)
Mid-point=\(\left ( 2\tfrac{1}{2},2\tfrac{1}{2} \right )\)
(ii)\(x^{2}-\left ( 4+m \right )x+4=0\rightarrow \left ( 4+m \right )^{2}-4(4)=0\)
\(4+m=\pm 4\) or \(m\left ( 8+m \right )=0\)
m=-8
\(x^{2}+4x+4=0\)
So, the coordinates of the point where the tangent touches the curve are
OR
2x-4=m
\(x^{2}-4x+4=\left ( 2x-4 \right )x\)
x=-2 (ignore +2)
m=-8(ignore 0)
y=16
Question
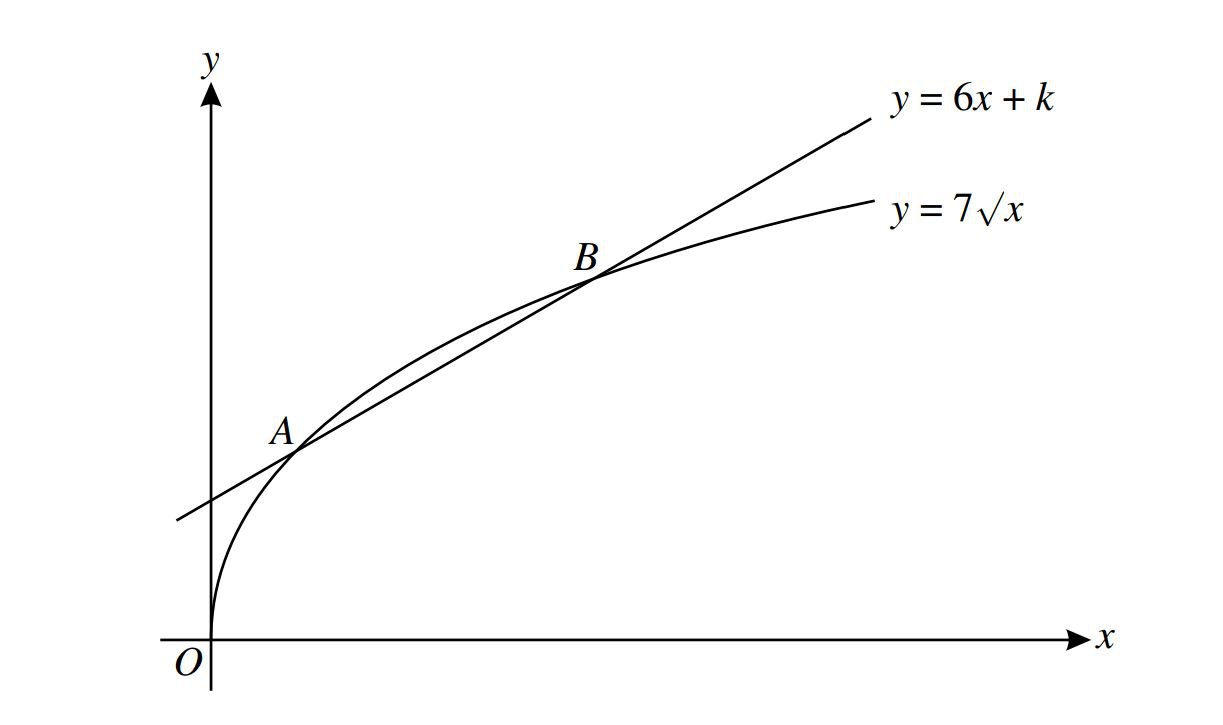
The diagram shows the curve and the line \(y=7\sqrt{x}\) and the line y=6c+k ,where k is a constant. The curve and the line intersect at the points A and B
(i)For the case where k=2,find the x-coordinates of A and B.
(ii)Find the value of k for which y=6x+k is a tangent to the curve \(y=7\sqrt{x}\)
▶️Answer/Explanation
(i)\(6x+2=7\sqrt{x}\Rightarrow 6\left ( \sqrt{x} \right )^{2}-7\sqrt{x}+2=0\)
\(\left ( 3\sqrt{x} -2\right )\left ( 2\sqrt{x} -1\right )=0\)
\(\sqrt{x}=\frac{2}{3}\) or \(\frac{1}{2}\)
\(x=\frac{4}{9}\) or \(\frac{1}{4}\0 (or 0.444,0.25)
OR
\(\left ( 6x+2 \right )^{2}=49x\rightarrow 36x^{2}-25x+4=0\)
\(\left ( 9x-4 \right )\left ( 4x-1 \right )=0\)
\(x=\frac{4}{9}\) or \(\frac{1}{4}\0 (or 0.444,0.25)
(ii)\(7^{2}-4\times6\times k=0\)
\(k=\frac{49}{24}\) or 2.04
OR
\(\frac{\mathrm{d} }{\mathrm{d} x}\left ( 7x^{\frac{1}{2}} \right )=\frac{\mathrm{d} }{\mathrm{d} x}\left ( 6x+k \right )\rightarrow \frac{7}{2}x^{-\frac{1}{2}}=6\)
\(x=\frac{49}{144},y=\frac{49}{12}\rightarrow k=\frac{49}{24}\) or 2.04
Question
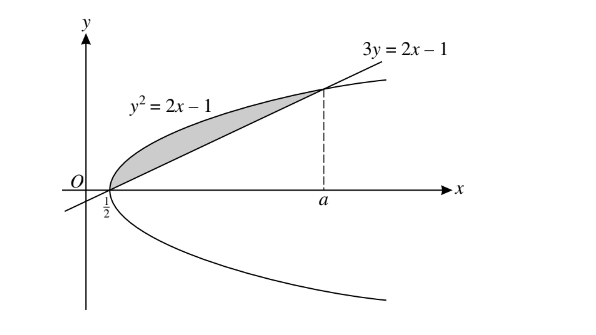
The diagram show the curve \(y^{2}=2x-1\) and the straight line 3y=2x-1.The curve and thew straight line intersect at \(x=\frac{1}{2}\) and x=a and ,where a is a constant.
(i)Show that a=5.
(ii)Find,showing all necessary working ,the area of the shaded region.
▶️Answer/Explanation
(i) To find the value of \(a\), we know that the curve \(y^2 = 2x – 1\) intersects the line \(3y = 2x – 1\) at \(x = \frac{1}{2}\) and \(x = a\).
First, substitute \(x = \frac{1}{2}\) into the equation of the line to find the corresponding \(y\):
\(3y = 2\left(\frac{1}{2}\right) – 1\)
\(3y = 0 \implies y = 0\)
So, at \(x = \frac{1}{2}\), the point of intersection is \(\left(\frac{1}{2}, 0\)\).
Now, substitute \(x = a\) into both equations:
\(y^2 = 2a – 1\)
\(3y = 2a – 1\)
\(2a – 1 = y^2\)
Now, substitute \(x = \frac{1}{2}\) and \(y = 0\):
\(2\left(\frac{1}{2}\right) – 1 = 0^2\)
This is true, confirming that \(x = \frac{1}{2}\). Therefore, \(a = 5\).
(ii) Now, we need to find the area of the shaded region. The shaded region is the area between the curve \(y^2 = 2x – 1\) and the line \(3y = 2x – 1\) from \(x = \frac{1}{2}\) to \(x = 5\).
The area \(A\) is given by the integral:
\(A = \int_{\frac{1}{2}}^5 \left(3y – \frac{1}{2}\right) \,dx\)
To find \(y\) in terms of \(x\), we use the equation \(3y = 2x – 1\), so \(y = \frac{2x – 1}{3}\).
Substitute this into the integral:
\(A = \int_{\frac{1}{2}}^5 \left(3 \cdot \frac{2x – 1}{3} – \frac{1}{2}\right) \dx\)
\(\left [ \frac{\left ( 2x-1 \right )^{\frac{3}{2}}}{\frac{3}{2}} \right ]\div 2\)
\(\left [ \frac{2}{3}\times \frac{x^{2}}{2}-\frac{x}{3} \right ]\)
\(\left [ \frac{27}{9}-0 \right ]\)
\( \left [ \frac{25}{3}-\frac{5}{3}-\left ( \frac{1}{12}-\frac{1}{6} \right ) \right ]\)
\(\frac{9}{4}\)