Question
The diagram shows the curve with equation \(y = 4x^{\frac{1}{2}}\)
(i) The straight line with equation \(y = x + 3\) intersects the curve at points A and B. Find the length
of AB.
(ii) The tangent to the curve at a point T is parallel to AB. Find the coordinates of T.
(iii) Find the coordinates of the point of intersection of the normal to the curve at T with the line AB.
▶️Answer/Explanation
(i) Length of AB:
We have the equation \(4x^{1/2} = x + 3\). Let’s solve this equation:
\( 16x = (x + 3)^2 \)
\( 16x = x^2 + 6x + 9 \)
\( x^2 – 10x +9 = 0 \)
Now, we can solve this quadratic equation using the quadratic formula:
\( x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \)
For our equation, \(a = 1\), \(b = -10\), and \(c = 9\).
\( x = \frac{10 \pm \sqrt{(-10)^2 – 4(1)(9)}}{2(1)} \)
\( x = \frac{10 \pm \sqrt{100-36}}{2} \)
\( x = \frac{10 \pm \sqrt{64}}{2} \)
\( x = \frac{10 \pm 2\sqrt{64}}{2} \)
\( x = \frac{10\pm 8}{2} \)
\(\x=frac{10+8}{2}\) and \(x= \frac{10-8}{2}\)
x=9 and x=1
So, we have two values for \(x\):9 and 1
Now, substitute these values into either the equation of the curve or the line to find the corresponding \(y\)-coordinates. Let’s use the equation of the curve:
\( y = 4x^{1/2} \)
For x=9
\( y = 4(9)^{1/2} \)
y=12
Similarly, for x=1
\( y = 4(1)^{1/2} \)
y=4
Now, we have the coordinates of points A and B. Use the distance formula to find the length of \(AB\):
\( \text{Length of } AB = \sqrt{(x_A – x_B)^2 + (y_A – y_B)^2} \)
\(AB=\sqrt{(9-1)^{2}+(12-4)^{2}}\)
\(AB=\sqrt{8^{2}+8^{2}}\)
\(AB=\sqrt{64+64}\)
\(AB=\sqrt{128}\)
\(AB=11.3\)
(ii) The tangent to the curve at point T is parallel to AB. For a parallel tangent, the slopes of the curve and the line are equal. Find the slope of the line \(y = x + 3\) (which is 1), and set it equal to the derivative of the curve’s equation with respect to \(x\):
\( \frac{dy}{dx} = \frac{d}{dx}(4x^{1/2}) \)
\( \frac{1}{2} \cdot 4x^{-1/2} = 1 \)
\( 2x^{-1/2} = 1 \)
\(x=4\)
Now substitute x into the curve equation:
\(y=4x^{\frac{1}{2}}\)
\(y=8\)
The coordinates \((4,8)\) are the coordinates of point T.
(iii)The equation of the normal is given by:
\( y – 8 = -1(x – 4) \)
Now, let’s eliminate \(y\) or \(x\):
\( -x + 12 = x + 3 \)
\( 2x = 9 \)
\( x = \frac{9}{2} \)
Now, substitute \(x\) back into the equation of the normal to find \(y\):
\( y – 8 = -1\left(\frac{9}{2} – 4\right) \)
\( y – 8 = -1\left(\frac{1}{2}\right) \)
\( y – 8 = -\frac{1}{2} \)
\( y = \frac{15}{2} \)
So, the point of intersection is \(\left(\frac{9}{2}, \frac{15}{2}\right)\), which is equivalent to \(\left(4^{\frac{1}{2}}, 7^{\frac{1}{2}}\right)\).
Question
A diameter of a circle \(C_1\) has end-points at (-3,-5) and (7,3).
(a) Find an equation of the circle \(C_1\).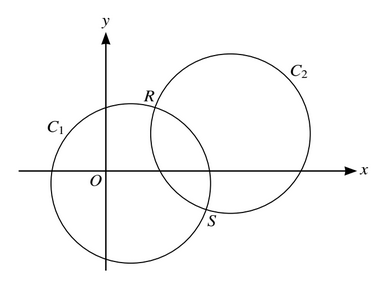
The circle \(C_1\) is translated by \(\binom{8}{4}\) to give circle \(C_2\), as shown in the diagram.
(b) Find an equation of the circle \(C_2\).
The two circles intersect at points R and S.
(c) Show that the equation of the line RS is y=-2x+13.
(d) Hence show that the x-coordinates of R and S satisfy the equation \(5x^2-60x+159=0\).
▶️Answer/Explanation
(a) Equation of Circle \(C_1\):
The equation of a circle with center \((h, k)\) and radius \(r\) is given by \((x – h)^2 + (y – k)^2 = r^2\).
Given the endpoints of the diameter \((-3, -5)\) and \((7, 3)\), the center \((h, k)\) is the midpoint of the diameter, which can be found as follows:
\( h = \frac{-3 + 7}{2} = 2 \)
\( k = \frac{-5 + 3}{2} = -1 \)
The radius \(r\) is the distance from the center to one of the endpoints. Using the distance formula:
\( r = \sqrt{(7 – 2)^2 + (3 – (-1))^2} = \sqrt{25 + 16} = \sqrt{41} \)
Therefore, the equation of circle \(C_1\) is:
\( (x – 2)^2 + (y + 1)^2 = 41 \)
(b) Equation of Circle \(C_2\):
The circle \(C_2\) is obtained by translating \(C_1\) by \(\begin{bmatrix} 8 \\ 4 \end{bmatrix}\). The center of \(C_2\) is the sum of the center of \(C_1\) and the translation vector:
\( \text{Center of } C_2 = \begin{bmatrix} 2 + 8 \\ -1 + 4 \end{bmatrix} = \begin{bmatrix} 10 \\ 3 \end{bmatrix} \)
The radius of \(C_2\) remains the same as \(C_1\), which is \(\sqrt{41}\). Therefore, the equation of \(C_2\) is:
\( (x – 10)^2 + (y – 3)^2 = 41 \)
(c)\((x-2)^2+(y+1)^2-41=(x-10)^2+(y-3)^2-41OE\)
\(x^2-4x+4+y^2+2y+1=x^2-20x+100+y^2-6y+9 OE\)
16x+8y=104
y=-2x+13
(d) \((x-10)^2(-2x+13-3)^2=41\)
\(x^2-20x+100+4x^2-40x+100=41 \rightarrow 5x^2-60x+159=0\)