Question
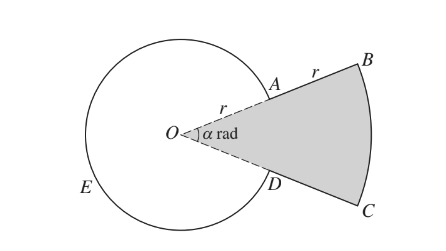
The diagram shows a metal plate made by fixing together two pieces, OABCD (shaded) and OAED (unshaded). The piece OABCD is a minor sector of a circle with centre O and radius 2r. The piece OAED is a major sector of a circle with centre O and radius r. Angle AOD is \(\alpha\) radians. Simplifying your answers where possible, find, in terms of \( \pi \) ,\(\alpha\) and r.
(i) the perimeter of the metal plate.
(ii) the area of the metal plate.
It is now given that the shaded and unshaded pieces are equal in area.
(iii) Find \(\alpha\) in terms of \(\pi \)
▶️Answer/Explanation
(i) Perimeter of the Metal Plate:
The perimeter of the metal plate consists of the lengths of the curved edges and the straight edge connecting the endpoints.
For the minor sector OABCD, the curved edge has an arc length equal to \(2r\) times the angle \(\alpha\). This is because the entire circumference of a circle with radius \(2r\) is \(2\pi \times 2r = 4\pi r\), and the angle \(\alpha\) is a fraction of the full circle. So, the arc length of the minor sector is \(2r \alpha\).
For the major sector OAED, the curved edge has an arc length equal to \(r\) times the angle \(\pi – \alpha\). Similarly, this is because the entire circumference of a circle with radius \(r\) is \(2\pi r\), and the angle \(\pi – \alpha\) is a fraction of the full circle. So, the arc length of the major sector is \(r (\pi – \alpha)\).
Finally, the straight edge connecting the endpoints has a length of \(2r\).
The total perimeter is the sum of these lengths:
\(P = 2\pi r + r\alpha + 2r\)
(ii)Area of the Metal Plate:
The area of the metal plate consists of the sum of the areas of the shaded and unshaded regions.
For the minor sector OABCD, the area is given by the formula for the area of a sector: \(\frac{1}{2}r^2\alpha\).
Since the radius is \(2r\), this becomes \(\frac{1}{2}(2r)^2 \alpha = 2r^2 \alpha\).
For the major sector OAED, the area is similarly given by \(\frac{1}{2}r^2 (\pi – \alpha)\).
The total area is the sum of these areas:
\(A = 2r^2 \alpha + \frac{1}{2}r^2 (\pi – \alpha)\)
(iii) Finding \(\alpha\) in terms of \(\pi\):
Given that the shaded and unshaded areas are equal, you set up the equation:
\(2r^2\alpha = \frac{1}{2}r^2(\pi – \alpha)\)
Solving for \(\alpha\),
\(\alpha = \frac{2}{5}\pi\)
Question
The function f is defined by \(f:x\rightarrow \frac{2}{3-2x}\) for \(x\epsilon R\) ,\(x\neq \frac{3}{2}\)
(i) Find an expression for \(f^{-1}\left ( x \right )\).
The function g is defined by \(g:x\rightarrow 4x+a\) for \(x\epsilon R\) ,where a is ac constant.
(ii)Find the value of a for which gf(-1)=3
(iii) Find the possible values of a given that the equation\( f^{-1}\left ( x \right )=g^{-1}\left ( x \right )\) has two equal roots.
▶️Answer/Explanation
(i) To find the inverse function $f^{-1}(x)$, switch $x$ and $y$ in the definition of $f$ and solve for $y$:
\(y = \frac{2}{3 – 2x}\)
\(x = \frac{2}{3 – 2y}\)
\(3 – 2y = \frac{2}{x}\)
\(2y = 3 – \frac{2}{x}\)
\(y = \frac{3}{2} – \frac{1}{x}\)
So, $f^{-1}(x) = \frac{3}{2} – \frac{1}{x}$.
(ii) To find the value of $a$ for which $\operatorname{gf}(-1) = 3$, first, find $g(f(-1))$:
\(g(f(-1)) = g\left(\frac{2}{3 – 2(-1)}\right)\)
\(= g\left(\frac{2}{5}\right)\)
\(4\left(\frac{2}{5}\right) + a = 3\)
\(\frac{8}{5} + a = 3\)
\(a = 3 – \frac{8}{5} = \frac{7}{5}\)
So, the value of $a$ is $\frac{7}{5}$.
(iii)\(g^{-1}(x) = \frac{x – a}{4} = f^{-1}(x)\)
This equation can be written as:
\(\frac{x – a}{4} = \frac{3}{2} – \frac{1}{x}\)
\(x – a = 6x – \frac{4}{x}\)
\(6x – x – a – \frac{4}{x} = 0\)
\(5x – a – \frac{4}{x} = 0\)
\(5x^2 – ax – 4 = 0\)
\((a + 6)^2 = a^2 + 12a + 36\)
So, the correct equation is \(a^2 + 12a + 36 = 16\) or \(a^2 + 12a + 20 = 0\).
We can use the quadratic formula to solve for \(a\):
\(a = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}\)
In this case, \(a^2 + 12a + 20 = 0\), so \(a = \frac{-12 \pm \sqrt{12^2 – 4(1)(20)}}{2(1)}\):
\(a = \frac{-12 \pm \sqrt{144 – 80}}{2}\)
\(a = \frac{-12 \pm \sqrt{64}}{2}\)
\(a = \frac{-12 \pm 8}{2}\)
This gives two possible values for \(a\):
\(a_1 = \frac{-12 + 8}{2} = -2\)
\(a_2 = \frac{-12 – 8}{2} = -10\)
So, the correct solutions for \(a\) are \(a = -2\) or \(a = -10\).
Question
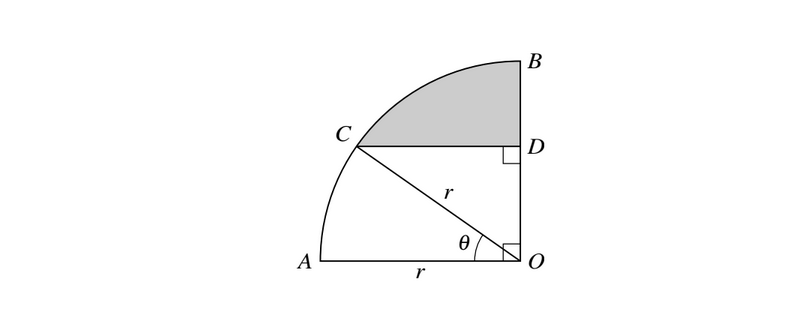
In the diagram, AOB is a quarter circle with centre O and radius r. The point C lies on the arc AB and the point D lies on OB. The line CD is parallel to AO and angle \(AOC = \Theta \)radians.
(i) Express the perimeter of the shaded region in terms of r,\(\Theta \)and \(\Pi\).
(ii) For the case where r = 5 cm and \(\Theta = 0.6\), find the area of the shaded region.
▶️Answer/Explanation
(i) Express the perimeter of the shaded region in terms of \(r\), \(\Theta\), and \(\pi\).
The shaded region consists of three parts: the quarter circle \(AOB\), the arc \(AC\), and the segment \(ABC\). The perimeter (\(P\)) is the sum of the lengths of these three parts.
Quarter Circle \(AOB\):The circumference of a full circle is \(2\pi r\), so the quarter circle has a circumference of \(\frac{1}{4} \cdot 2\pi r = \frac{1}{2}\pi r\).
Arc \(AC\):The length of the arc \(AC\) can be found using the formula for the circumference of a circle and the fraction of the circle represented by the angle \(\Theta\):
\[ \text{Arc length} = \frac{\Theta}{360^\circ} \cdot 2\pi r \]
Segment \(ABC\):The length of \(CD\) is \(r\) (as \(CD\) is parallel to \(AO\)). The length of \(AB\) is \(r\Theta\) (as \(AB\) is a fraction of the circumference corresponding to the angle \(\Theta\)). So, the length of \(BC\) is \(r\Theta – r\).
\[ P = \frac{1}{2}\pi r + \frac{\Theta}{360^\circ} \cdot 2\pi r + (r\Theta – r) \]
\[ P = \frac{1}{2}\pi r + \frac{\Theta}{180^\circ} \cdot \pi r + r\Theta – r \]
(ii) Area \(A):
In this case, we’re finding the area of the shaded region, which consists of the quarter circle \(AOB\) and the segment \(ABC\).
Quarter Circle \(AOB\):
– The area of a quarter circle is given by \(\frac{1}{4}\pi r^2\).
\( \text{Area of quarter circle} = \frac{1}{4}\pi \cdot (5 \, \text{cm})^2 = \frac{1}{4}\pi \cdot 25 = \frac{25}{4}\pi \, \text{cm}^2 \)
Segment \(ABC\):
– The area of a segment can be found by subtracting the area of the corresponding triangle from the area of the sector.
Sector Area:
– The area of the sector is given by \(\frac{1}{2} r^2 \left(\frac{1}{2}\pi – \Theta\right)\).
\( \text{Sector area} = \frac{1}{2} \cdot (5 \, \text{cm})^2 \cdot \left(\frac{1}{2}\pi – 0.6\right) \)
Triangle Area:
– The triangle is formed by \(O\), \(C\), and a point on the circle. The area of the triangle is given by \(\frac{1}{2} \cdot r \cdot \cos \Theta \cdot \frac{1}{2} \cdot r \cdot \sin \Theta\).
\( \text{Triangle area} = \frac{1}{2} \cdot 5 \, \text{cm} \cdot \cos 0.6 \cdot \frac{1}{2} \cdot 5 \, \text{cm} \cdot \sin 0.6 \)
Segment Area:
– Subtract the triangle area from the sector area to get the area of the segment.
\( \text{Segment area} = \text{Sector area} – \text{Triangle area} \)
Now, add the area of the quarter circle and the area of segment \(ABC\) to find the total area \(A\):
\( A = \frac{25}{4}\pi + \left(\frac{1}{2} \cdot (5)^2 \cdot \left(\frac{1}{2}\pi – 0.6\right) – \frac{1}{2} \cdot 5 \cdot \cos 0.6 \cdot \frac{1}{2} \cdot 5 \cdot \sin 0.6\right) \)
\( A \approx 6.31 \, \text{cm}^2 \)