Question
(i)Prove the identity \(\frac{\sin \Theta }{1-\cos \Theta }-\frac{1}{\sin \Theta }=\frac{1}{\tan \Theta }\).
(ii) Hence solve the equation \(\frac{\sin \Theta }{1-\cos \Theta }-\frac{1}{\sin \Theta }=4\tan \Theta \) for \(0^{\circ}< \Theta < 180^{\circ}\).
▶️Answer/Explanation
(i) Solvung LHS
\( \frac{\sin \Theta}{1 – \cos \Theta} – \frac{1}{\sin \Theta} \)
\( = \frac{\sin^2 \Theta – (1 – \cos \Theta)}{(1 – \cos \Theta)\sin \Theta} \)
\(= \frac{\sin^2 \Theta – 1 + \cos \Theta}{(1 – \cos \Theta)\sin \Theta} \)
\( = \frac{1 – \cos^2 \Theta – 1 + \cos \Theta}{(1 – \cos \Theta)\sin \Theta} \)
\( = \frac{\cos \Theta – \cos^2 \Theta}{(1 – \cos \Theta)\sin \Theta} \)
\( = \frac{\cos \Theta(1 – \cos \Theta)}{(1 – \cos \Theta)\sin \Theta} \)
\( = \frac{\cos \Theta}{\sin \Theta} \)
\( = \frac{1}{\tan \Theta} \)
(ii) \( \frac{1}{\tan \Theta} = 4 \tan \Theta \)
\( 1 = 4 \tan^2 \Theta \)
\( \tan^2 \Theta = \frac{1}{4} \)
\( \tan \Theta = \pm\frac{1}{2} \)
\(\Theta =26.6^{\circ}, 153.4^{\circ}\)
Question
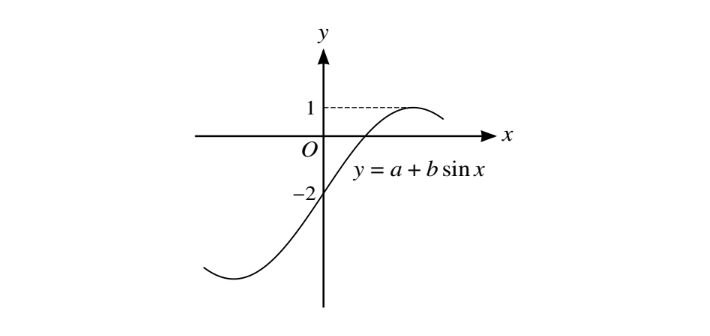
(a)The diagram shows part of the graph of \(y=a+b\sin x\).Find the values of constant a and b.
(b)(i)Show that the equation \(\left ( \sin \Theta +2\cos \Theta \right )\left ( 1+\sin \Theta -\cos \Theta \right )=\sin \Theta \left ( 1+\cos \Theta \right )\)
may be expressed as \(3\cos ^{2}\Theta -2\cos \Theta -1=0\).
(c)Hence solve the equation \(\left ( \sin \Theta +2\cos \Theta \right )\left ( 1+\sin \Theta-\cos \Theta \right )=\sin \Theta \left ( 1+\cos \Theta \right )\) for \(-180^{\circ}\leq \Theta \leq 180^{\circ}\)
Answer/Explanation
(i)a=-2,b=3
(b)(ii)\(s+s^{2}-sc+2c+2sc=s+sc\rightarrow s^{2}-2c^{2}+2c=0\)
\(1-\cos ^{2}\Theta -2\cos ^{2}\Theta +2\cos \Theta =0\)
\(3\cos ^{2}\Theta -2\cos \Theta -1=0\)
(ii)\(\cos \Theta = 1\)or \( -\frac{1}{3}\)
\(\Theta =0^{\circ}\) or \(109.5^{\circ}\) or \(-109.5^{\circ}\)
Question
(i) Show that the equation \( \frac{4\cos \Theta }{\tan \Theta }+15=0\) can be expressed as \(4\sin ^{2}\Theta -15\sin \Theta -4=0\).
(ii) Hence solve the equation \(\frac{4\cos \Theta }{\tan \Theta }+15=0\) for \(0^{\circ}\leq \Theta \leq 360^{\circ}\).
Answer/Explanation
(i)\(4\cos ^{2}\Theta +15\sin \Theta =0\)
\(4(1-s^{2})+15s=0\rightarrow 4\sin ^{2}\Theta -15\sin \Theta -4=0\)
(ii)\(\sin \Theta =-\frac{1}{4}\)
\(\Theta \)=194.5 or 345.5