Question
The equation of a curve is
y3 + 4xy = 16.
(i) Show that \(\frac{dy}{dx}=-\frac{4y}{3y^{2}+4x}\). [4]
(ii) Show that the curve has no stationary points. [2]
(iii) Find the coordinates of the point on the curve where the tangent is parallel to the y-axis. [4]
Answer/Explanation
Ans:
7 (i) Obtain \(3y^{2}\frac{dy}{dx}\) as derivative of y3
Obtain \(4y+4x\frac{dy}{dx}\) as derivative of 4xy
Equate derivative of left-hand side to zero and solve for \(\frac{dy}{dx}\), must be from implicit differentiation
Confirm given answer \(\frac{dy}{dx}=-\frac{4y}{3y^{2}+4x}\) correctly
(ii) State or imply y = 0
Substitute in equation of curve and show contradiction
(iii) State or imply \(3y^{2}+4x=0\)
Eliminate one variable from equation of curve using \(3y^{2}+4x=0\)
Obtain y = −2
Obtain x = −3
Question
The equation of a curve is
y = 6 sin x − 2 cos 2x.
Find the equation of the tangent to the curve at the point \(\left ( \frac{1}{6}\pi ,2 \right )\). Give the answer in the form y = mx + c, where the values of m and c are correct to 3 significant figures. [5]
Answer/Explanation
Ans:
3 Differentiate to obtain form p cos x + q sin 2 equivalent
Obtain correct 6 cos x + 4sin 2x or equivalent
Substitute \(\frac{1}{6}\pi \) to obtain derivative equal to \(5\sqrt{3}\) or 8.66
Form equation of tangent (not normal) using numerical value of gradient obtained by differentiation
Obtain y = − 8.66 x – 2.53 cao
Question
The equation of a curve is \(y=\frac{1}{2}e^{2x}-5e^{x}+4x\). Find the exact x-coordinate of each of the stationary points of the curve and determine the nature of each stationary point.
Answer/Explanation
Obtain derivative \(e^{2x}-5e^{x}+4\)
Equate derivative to zero and carry out recognisable solution method for a quadratic in \(e^{x}\)
Obtain \(e^{x}=1\) or \(e^{x}=4\)
Obtain x = 0 and \(x=\ln 4\)
Use an appropriate method for determining nature of at least one stationary point
\(\left ( \frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=2e^{2x} -5e^{x},when x=0,\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=-3,x=\ln 4,\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=+12\right )\)
Conclude maximum at x = 0 and minimum at x = ln 4 (no errors seen)
Question
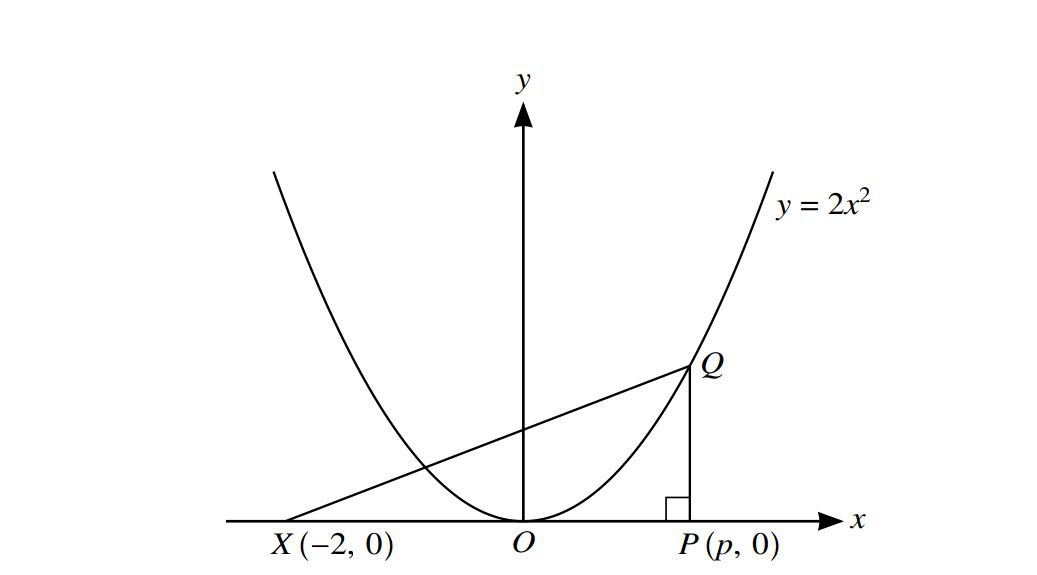
The diagram shows the curve \(y=2x^{2}\) and the points X(-2,0) and P(p,0).The point Q lies on the curve and PQ is parallel to the y-axis.
(i)_Express the area,A,of trioangle XPQ in terms of p.
The point P moves along the x-axis at a constant rate of 0.02 units per second and Q moves along the curve so that PQ remains to the y-axis.
(ii)Find the rate at which A is increasing when p=2.
Answer/Explanation
(i)\(A=\frac{1}{2}\times \left ( 2+p \right )\times 2p^{2}=2p^{2}+p^{3}\)
(ii)\(\frac{\mathrm{d} A}{\mathrm{d} p}=4p+3p^{2}\)
\(\frac{\mathrm{d} A}{\mathrm{d} t}=\frac{\mathrm{d} A}{\mathrm{d} p}\times \frac{\mathrm{d} p}{\mathrm{d} t}=0.02\times 20=0.4\)
or\( \frac{\mathrm{d} A}{\mathrm{d} t}=4p\frac{\mathrm{d} p}{\mathrm{d} t}+3p^{2}\frac{\mathrm{d} p}{\mathrm{d} t}\)
Question
The line with gradient -2 passing through the point P(3t,2t)intersects the x-axis at A and the y-axis at B.
(i)Find the area of triangle AOB in terms of t.
(ii)The line through P perpendicular to AB intersects the x-axis at C.
Show that the mid-point of PC lies on the line y=x.
Answer/Explanation
(i)\(y-2t=-2(x-3t)\rightarrow y+2x=8t\)
Set x to 0→B(0,8t)
Set y to 0→A(4t,0)
\(\rightarrow Area=16t^{2}\)
(ii)\(m=\frac{1}{2}\)
\(\rightarrow y-2t=\frac{1}{2}(x-3t)\rightarrow 2y=x+t\)
Set y to 0\(\rightarrow C(-t,0)\)
Mid point of Cp is (t,t)
This lies on the line y=x.
Question
The equation of a curve is \(y=x^{3}+px^{2}\) ,where p is a positive constant .
(i)Show that the origin is a stationary point on the curve and find the coordinates of the other stationary point in terms of p.
(ii)Find the nature of each of the stationary points.
Another curve has equation \(y=x^{3}+px^{2}+px\)
(iii)Find the set of values of p for which this curve has n o stationary points.
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=3x^{2}+2px\)
Sets to 0\(\rightarrow x=0\) or \(-\frac{2p}{3}\)
→(0,0) or\((\frac{2p}{3},\frac{4p^{3}}{27})\)
(ii)\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=6x+2p\)
At (0,0)→2p positive Minimum
At\((\frac{2p}{3},\frac{4p^{3}}{27})\)→-2p -ve Maximum
(iii)\(y=x^{3}+px^{2}+px\rightarrow 3x^{2}+2px+p=0\)
Uses \(b^{2}-4ac\)
\(\rightarrow 4p^{2}-12p< 0\)
\(\rightarrow 0< p< 3\)
Question
A curve is such that \(\frac{\mathrm{d} y}{\mathrm{d} x}=x^{\frac{1}{2}}-x^{-\frac{1}{2}}\) .The curve passes through the point \(\left ( 4,\frac{2}{3} \right )\)
(i)Find the equation of the curve .
(ii)Find \(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}\)
(iii)Find the coordinates of the stationary point and determine its nature.
Answer/Explanation
(i)\(y=\frac{2}{3}x^{\frac{3}{2}}-2x^{\frac{1}{2}}+c\)
\(\frac{2}{3}=\frac{16}{3}-4+c\)
\(c=-\frac{2}{3}\)
(ii)\(\frac{1}{2}x^{-\frac{1}{2}}+\frac{1}{2}^{-\frac{3}{2}}\)
(iii)\(x^{\frac{1}{2}}-x^{-\frac{1}{2}}=0\)\(\rightarrow \frac{x-1}{\sqrt{x}}=0\)
x=1
When x=1,\(y=\frac{2}{3}-2-\frac{2}{3}=-2\)
When x=1 ,\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=1> 0\) Hence minimum
Question
A line has equation y=2x+c and a curve has equation \(y=8-2x-x^{2}\).
(i)For the case where the line is a tangent to the curve ,find the value of the constant c.
(ii)For the case wjhere c=11,find the x-coordinates of the points of intersection of the line and the curve.Find also, by integration, the area of the region between the line and the curve.
Answer/Explanation
(i)\(x^{2}+4x+c-8=0\)
\(16-4(c-8)=0\)
c=12
OR
\(-2-2x=2\rightarrow x=-2\)
-4+c=8+4-4
c=12
(ii)\(x^{2}+4x+3\rightarrow \left ( x+1 \right )\left ( x+3 \right )=0\)
x=-1 or -3
\(\int \left ( 8-2x-x^{2} \right )-\left [ \int \left ( 2x+11 \right ) \right ]\) or area of trapezium
\(\left [ 8x-x^{2}-\frac{x^{3}}{3} \right ]-\left [ x^{2}+11x \right ]\) or \(\left [ 8x-x^{2}-\frac{x^{3}}{3} \right ]-\frac{1}{2}\left ( 5+9 \right )\times 2\)
Apply their limits to at least integral for curve \(1\tfrac{1}{3}\)
Question
A curve has equation .Find the equation \(\left ( \frac{4}{\left ( 3x+1 \right )^{2}} \right )\) of the tangent to the curve at the point at the point where the line x=-1 intersects the curve.
Answer/Explanation
\(frac{\mathrm{d} y}{\mathrm{d} x}=\left [ -2\times 4\left ( 3x+1 \right ) ^{-3}\right ]\times 3\)
When x=-1 ,\(\frac{\mathrm{d}y }{\mathrm{d} x}=3\)
When x=-1,y=1
\(y-1=3\left ( x+1 \right )\rightarrow y=3x+4\)
Question
A curve has equation \(y=f\left ( x \right )\) and is such that \(f{}’\left ( x \right )=3x^{\frac{1}{2}}+3x^{-\frac{1}{2}}-10\).
(i)By using the substitution ,or ot6herwise,find the value of x for which the curve y=f(x has stationary points.
(ii) Find and hence ,or otherwise ,determine the nature of each stationary point.
(iii)It is given that the curve y=f(x) passes through the point (4,-7) .Find f(x).
Answer/Explanation
(i)\(3u+\frac{3}{u}-10=0\)
\(3u^{2}-10u+3=0\Rightarrow \left ( 3u-1 \right )\left ( u-3 \right )=0\)
\(\sqrt{x}=\frac{1}{3}\) or 3
\(\sqrt{x}=\frac{1}{9}or 9\)
(ii)\(f{}”\left ( x \right )=\frac{3}{2}x^{-\frac{1}{2}} -\frac{3}{2} x^{-\frac{3}{2}} \)
At \(x=\frac{1}{9}\)
\(f{}”\left ( x \right )=\frac{3}{2}\left ( 3 \right )-\frac{3}{2}\left ( 27 \right )=-36< 0\rightarrow\)Max
At x=9
\(f{}”\left ( x \right )=\frac{3}{2}\times \frac{1}{3}-\frac{3}{2}\times \frac{1}{27}=\frac{4}{9}> 0\rightarrow\)Min
(iii)\(f(x)=2x^{\frac{3}{2}}+6x^{\frac{1}{2}}-10x(+c)\)
-7=16+12-40+c
c=5
Question
(i)Express \(2x^{2}-12x+13\) in the form \(a\left ( x+b \right )^{2}+c\) where a,b and c are constants.
(ii)The function f is defined by \(f\left ( x \right )=2x^{2}-12x+13 \) for \( x\geq k\) where k is a constant.It is given that f is a one-one function.State the smallest possible value of k.
The value of k is now given to be 7.
(iii) Find the range of f.
(iv) Find an expression for \(f^{-1}\left ( x \right )\) and state the domain of \(f^{-1}\).
Answer/Explanation
(i) \(2\left ( x-3 \right )^{2}-5\) or a=2,b=-3,c=-5
(ii) 3
(iii)\(\left ( y \right )\geq 27\)
(iv)\(2\left ( x-3 \right )^{2}=\left ( y+5 \right )\)
\(x-3=\left ( \pm \right )\sqrt{\frac{1}{2}\left ( y+5 \right )}\)
\(x=3+\left ( \pm \right )\sqrt{\frac{1}{2}\left ( y+5 \right )}\)
\(\left ( f^{-1}\left ( x \right ) \right )=3+\sqrt{\frac{1}{2}\left ( x+5 \right )}\) for \(x\geq 27\)
Question
Question
A curve has equation \(y=x^{2}-4x+4 \) and a line has equation y=mx ,where m is a constant.
(i)For the case where m=1,the curve and the line intersect at the points A and B.Find the coordinates of mid-point of AB.
(ii)Find the non-zero value of m for which the line is a tangent to the curve ,and find the coordinates of the point where the tangent touches the curve.
Answer/Explanation
(i)\(x^{2}-4x+4=x\Rightarrow x^{2}-5x+4=0\)
\(\left ( x-1 \right )\left ( x-4 \right )=0\)
(1,1),(4,4)
Mid-point=\(\left ( 2\tfrac{1}{2},2\tfrac{1}{2} \right )\)
(ii)\(x^{2}-\left ( 4+m \right )x+4=0\rightarrow \left ( 4+m \right )^{2}-4(4)=0\)
\(4+m=\pm 4\) or \(m\left ( 8+m \right )=0\)
m=-8
\(x^{2}+4x+4=0\)
x=-2,y=16
(ii)2x-4=m
\(x^{2}-4x+4=\left ( 2x-4 \right )x\)
x=-2 (ignore +2)
m=-8(ignore 0)
y=16
Question
It is given that \(f\left ( x \right )=\left ( 2x-5 \right )^{3}\) for \(x\epsilon R\) .Show that f is an increasing function.
Answer/Explanation
\(f{}'(x)=\left ( 2x-5 \right )^{2}\times 2+1\) or \(24\left ( x-\frac{5}{2} \right )^{2}+1\)
\(> 0(allow \geq 0)\)
Question
It is given that a curve has equation \(y=f\left ( x \right )\) ,where \(f\left ( x \right )=x^{3}-2x^{2}+x\)
(i)Find the set of values of x for which the gradient of the curve is less than 5.
(ii)Find the values of f(x) at the two stationary points on the curve and determine the nature if each stationary point.
Answer/Explanation
(i)\(3x^{2}-4x+1< 5\)
\(\left ( 3x+2 \right )\left ( x-2 \right )< 0\)
\(-\frac{2}{3}< x< 2\) or \(\left [ -\frac{2}{3} ,2\right ]\) or \(\left ( -\frac{2}{3} ,2\right )\)
(ii)\(3x^{2}-4x+1=0\Rightarrow \left ( 3x-1 \right )\left ( x-1 \right )=0\)
\(x=\frac{1}{3}\) or 1
\(y=\frac{4}{27} or 0
\(f{}”\left ( x \right )=6x-4\rightarrow f{\left ( \frac{1}{3} \right )}”=-2< 0\)
\(f{}”\left ( 1 \right )=2> 0\)
max at \(\left ( \frac{1}{3},\frac{4}{27} \right )\) ;min at (1,0)
Question
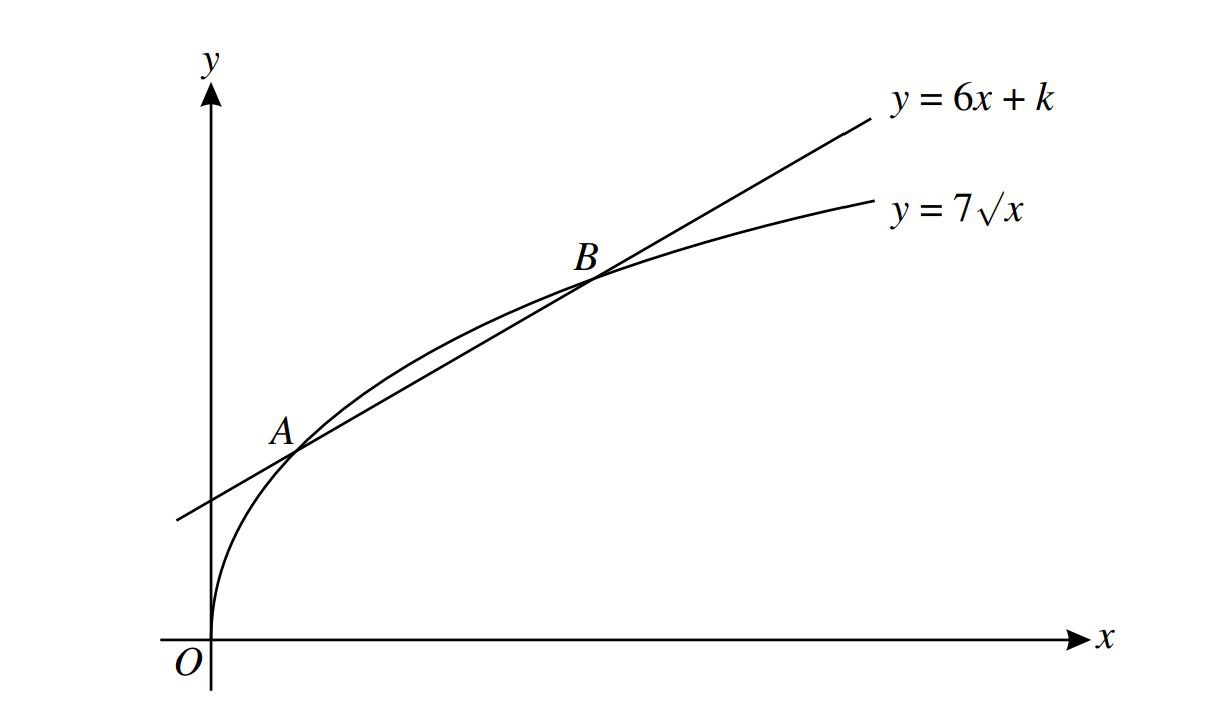
The diagram shows the curve and the line \(y=7\sqrt{x}\) and the line y=6c+k ,where k is a constant. The curve and the line intersect at the points A and B
(i)For the case where k=2,find the x-coordinates of A and B.
(ii)Find the value of k for which y=6x+k is a tangent to the curve \(y=7\sqrt{x}\)
Answer/Explanation
(i)\(6x+2=7\sqrt{x}\Rightarrow 6\left ( \sqrt{x} \right )^{2}-7\sqrt{x}+2=0\)
\(\left ( 3\sqrt{x} -2\right )\left ( 2\sqrt{x} -1\right )=0\)
\(\sqrt{x}=\frac{2}{3}\) or \(\frac{1}{2}\)
\(x=\frac{4}{9}\) or \(\frac{1}{4}\0 (or 0.444,0.25)
OR
\(\left ( 6x+2 \right )^{2}=49x\rightarrow 36x^{2}-25x+4=0\)
\(\left ( 9x-4 \right )\left ( 4x-1 \right )=0\)
\(x=\frac{4}{9}\) or \(\frac{1}{4}\0 (or 0.444,0.25)
(ii)\(7^{2}-4\times6\times k=0\)
\(k=\frac{49}{24}\0 or 2.04
OR
\(\frac{\mathrm{d} }{\mathrm{d} x}\left ( 7x^{\frac{1}{2}} \right )=\frac{\mathrm{d} }{\mathrm{d} x}\left ( 6x+k \right )\rightarrow \frac{7}{2}x^{-\frac{1}{2}}=6\)
\(x=\frac{49}{144},y=\frac{49}{12}\rightarrow k=\frac{49}{24}\) or 2.04
Question
A watermelon is assumed to be spherical in shape while it is growing .Its mass Mkg ,and radius, rcm ,are related by the formula \(M=kr^{3}\),where k is a constant .It is also assumed that the radius is increasing at a constant rate of 0.1 centimeters per day.On a particular day the radius is 10cm and the mass is 3.2kg.Find the value of k and the rate at which the mass is increasing on this day.
Answer/Explanation
\(1000k=3.2\Rightarrow k=\frac{3.2}{1000}\) or \(\frac{2}{625}\) or 0.0032
\(\frac{\mathrm{d}M }{\mathrm{d} r}=3kr^{2}\)
\(\frac{\mathrm{d}M }{\mathrm{d} t}=\frac{\mathrm{d} M}{\mathrm{d} r}\times \frac{\mathrm{d} r}{\mathrm{d} t}\) used e.g. \(3\times k\times 10^{2}\times 0.1\)
0.096
Question
The point P(3,5) lies on the curve \(y=\frac{1}{x-1}-\frac{9}{x-5}\)
(i)Find the x-coordinate of the point where the normal to the curve at P intersects the x-axis.
(ii)Find the x-coordinates of each of the stationary points on the curve and determine the nature of each stationary point,justifying your answer.
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=-(x-1)^{-2}+9(x-5)^{-2}\)
\(m_{tangent}=-\frac{1}{4}+\frac{9}{4}=2\)
\(Equation of normal is y-5=-\frac{1}{2}\left ( x-3 \right )\)
x=13
(ii)\(\left ( x-5 \right )^{2}=9\left ( x-1 \right )^{2}\)
\(x-5=\left ( \pm \right )3\left ( x-1 \right )\) or \(\left ( x^{2}-x-2 \right )=0\)
x=-1 or 2
\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=2\left ( x-1 \right )^{-3}-18\left ( x-5 \right )^{-3}\)
When x=-1,\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=-\frac{1}{6} < 0\) MAX
When x=2 \(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=\frac{8}{3} > 0\) MIN
Question
Machines in a factory make cardboard cones of base radius r cm and vertical height h cm .The volume, \(Vcm^{3}\),of such a cone is given by \(V=\frac{1}{3}\pi r^{2}h\).The machines produce comes for which h+r=18
(i)Show that \(V=6\pi r^{2}-\frac{1}{3}\pi r^{3}\)
(ii)Given that r can vary ,find the non-zero value of r for which V has a stationary value and show that the stationary value is a maximum.
(iii)Find the maximum volume of a cone that can be made by these machines.
Answer/Explanation
(i)\( V=\frac{1}{3}\pi r^{2}\left ( 18-r \right )=6\pi r^{2}-\frac{1}{3}\pi r^{3}\)
(ii)\(\frac{\mathrm{d} V}{\mathrm{d} x}=12\pi r-\pi r^{2}=0\)
\(\pi r\left ( 12-r \right )=0\rightarrow r=12\)
\(\frac{\mathrm{d} ^{2}V}{\mathrm{d} x^{2}}=12\pi -2\pi r\)
Sub \(r=12\rightarrow 12\pi -24\pi =-12\pi \rightarrow MAX\)
(iii)Sub r=12,h=6 \(\rightarrow MaxV=288\pi \) or 905
Question
A function f is defined by\( f:x\rightarrow x^{3}-x^{2}-8x+5\) for \(x< a\).It is given that f is an increasing function.Find the largest possible value of the constant a.
Answer/Explanation
\(f{}’\left ( x \right )=3x^{2}-2x-8\)
\(-\frac{4}{3}\),2 SOI
\(f{}’\left ( x \right )> 0\Rightarrow x< -\frac{4}{3}\)
Largest value of a is \(-\frac{4}{3}\)
Question
A curve has equation \(y=2x^{\frac{3}{2}}-3x-4x^{\frac{1}{2}}+4\).Find the equation of the tangent to the curve at the point (4,0)
Answer/Explanation
\(\frac{\mathrm{d} y}{\mathrm{d} x}=3x^{\frac{1}{2}}-3-2x^{-\frac{1}{2}}\)
at x=4 \(\frac{\mathrm{d} y}{\mathrm{d} x}=6-3-1=2\)
Equation of tangent is \(y=2\left ( x-4 \right )\)
Question
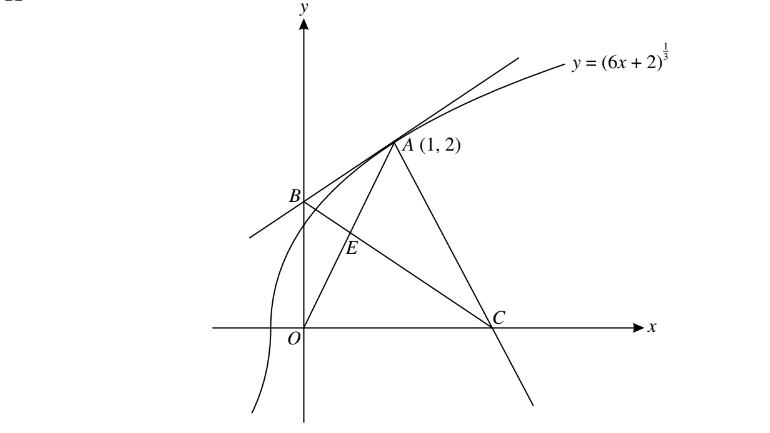
The diagram shows the curve \(y=\left ( 6x+2 \right )^{\frac{1}{3}}\) and the point A(1, 2) which lies on the curve. The tangent to the curve at A cuts the y-axis at B and the normal to the curve at A cuts the x-axis at C.
(i) Find the equation of the tangent AB and the equation of the normal AC.
(ii) Find the distance BC
(iii) Find the coordinates of the point of intersection, E, of OA and BC, and determine whether E is the mid-point of OA.
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=6\times \left [ \frac{1}{3}(6x+2)^{-\frac{2}{3}} \right ]\)
Equation of tangent is y-2=m(x-1)
Equation of normal is \(y-2=-\frac{1}{m}(x-1)\)
Both equation correct with \(m=\frac{1}{2}\)
(ii)\(B=\left ( 0,1\tfrac{1}{2} \right )\) ; C=(2,0)
\(y=-\frac{3}{4}(x-2)\)
Intersection(E):-\(\frac{3}{4}x+1\tfrac{1}{2}=2x\)
\(x=\frac{6}{11}\);\(y=\frac{12}{11}\)
Mid-point of OA=\(\left ( \frac{1}{2},1 \right )\)→E not mid-point
Question
A curve has equation .Verify that the \(y=2x+\frac{1}{\left ( x-1 \right )^{2}}\) curve has a stationary point at x=2 and determine its nature.
Answer/Explanation
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2-2(x-1)^{-3}\)
Sub \(x=2\rightarrow \frac{\mathrm{d} y}{\mathrm{d} x}=2-2=0\Rightarrow \)stat value at x=2
\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=6(x-1)^{-4}\) ( and sub at x=2
(At x=2,\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=6\)>0⇒Minimum
Question
An oil pipeline under the sea is leaking oil and a circular patch of oil has formed on the surface of the sea.At midday the radius of the patch of oil is 50m and is increasing at a rate of 3 metres per hour.FInd the rate at which the area of the oil is increasing at midday.
Answer/Explanation
\(A=\pi r^{2}\rightarrow (\frac{\mathrm{d} A}{\mathrm{d} r})=2\pi r\)
\(\frac{\mathrm{d} A}{\mathrm{d} t}=\frac{\mathrm{d} A}{\mathrm{d} r}\times \frac{\mathrm{d} r}{\mathrm{d} t}\)
\(\frac{\mathrm{d} r}{\mathrm{d} t}=3\)
\(300\pi\)
Question
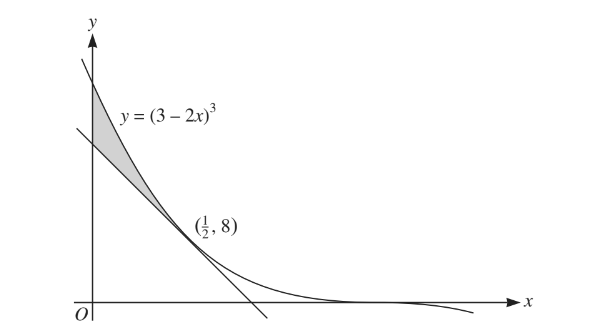
The diagram shows the curve \(y=\left ( 2-3x \right )^{3}\) and the tangent to the curve at the point \(\left ( \frac{1}{2},8 \right )\)
(i) Find the equation of this tangent, giving your answer in the form y = mx + c.
(ii) Find the area of the shaded region.
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=\left [ 3(3-2x)^{2} \right ]\times \left [ -2 \right ]\)
At \(x=\frac{1}{2}\) ,\(\frac{\mathrm{d} y}{\mathrm{d} x}=-24\)
\(y-8=-24(x-\frac{1}{2})\)
y=-24x+20
(ii)Area under curve=\(\left [ \frac{(3-2x)^{4}}{4} \right ]\times \left [ -\frac{1}{2} \right ]\)
\(-2-(-\frac{81}{8})\)
Area under tangent=\(\int \left ( -24x+20 \right )\)
\(=\left | -12x^{2}+20x \right |\) or 7
\(\frac{9}{8}\) or 1.125
Question
(a) In an arithmetic progression the sum of the first ten terms is 400 and the sum of the next ten terms is 1000. Find the common difference and the first term.
(b) A geometric progression has first term a, common ratio r and sum to infinity 6. A second geometric progression has first term 2a, common ratio \(r^{2}\) and sum to infinity 7. Find the values of a and r.
Answer/Explanation
(a)\(\frac{10}{2}(2a+9d)=400\)
\(\frac{20}{2}(2a+19d)=1400\)
\(\frac{10}{2}\left [ 2(a+10d)+9d \right ]=1000\)
d=6 a=13
(b)\(\frac{a}{1-r}=6 \) \(\frac{2a}{1-r^{2}}=7\)
\(\frac{12(1-r)}{1-r^{2}}=7\) or \(\frac{1-r^{2}}{1-r}=\frac{12}{7}\)
\(r=\frac{5}{7}\) or 0.714
\(a=\frac{12}{7}\) or 1.714
Question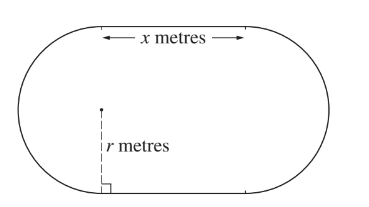
The inside lane of a school running track consists of two straight sections each of length x metres, and two semicircular sections each of radius r metres, as shown in the diagram. The straight sections are perpendicular to the diameters of the semicircular sections. The perimeter of the inside lane is 400 metres.
(i) Show that the area, \(Am^{2}\) , of the region enclosed by the inside lane is given by \(A=400r-\pi r^{2}\)
(ii) Given that x and r can vary, show that, when A has a stationary value, there are no straight sections in the track. Determine whether the stationary value is a maximum or a minimum.
Answer/Explanation
(i)\(A=2xr+\pi r^{2}\)
\(2x+2\pi r=400\Rightarrow x=200-\pi r\)
\(A=400r-\pi r^{2}\)
(ii) \(\frac{\mathrm{d} A}{\mathrm{d} r}=400-2\pi r=0\)
\(r=\frac{200}{\pi }\)
x=0⇒no straight sections
\(\frac{\mathrm{d} ^{2}A}{\mathrm{d} r^{2}}=-2\pi\)
Question
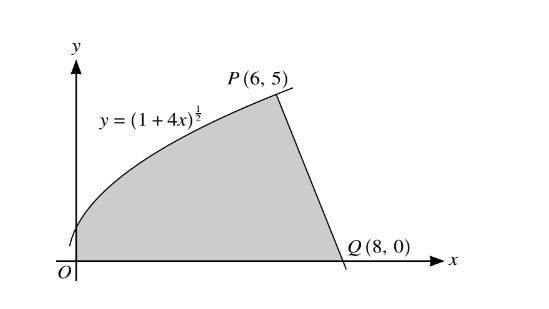
The diagram shows part of the curve \(\left ( 1+4x \right )^{\frac{1}{2}} \) and a point P (6, 5) lying on the curve. The line PQ intersects the x-axis at Q (8, 0).
(i) Show that PQ is a normal to the curve.
(ii) Find, showing all necessary working, the exact volume of revolution obtained when the shaded region is rotated through \(360^{\circ}\) about the x-axis. In part (ii) you may find it useful to apply the fact that the volume, V, of a cone of base radius r and vertical height h, is given by \(V=\frac{1}{3}\pi r^{2}h\).
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=\left [ \frac{1}{2}(1+4x)^{-\frac{1}{2}} \right ]\times 4\)
At x=6 ,\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2}{5}
Gradient of PQ\(=-\frac{5}{2}\) hence PQ is a normal or \(m_{1}m_{2}=-1\)
(ii)Volume for curve=\(\pi \int (1+4x)\) and attempt to integrate \(y^{2}\)
\(=\pi \left [ x+2x^{2} \right ]\)
\(=\pi \left [ 6+72-0 \right ]\)
\(=78(\pi )\)
Vol for line \(=\frac{1}{3}\times \pi \times 5^{2}\times 2\)
\(=\frac{50}{3}\pi \)
Total volume \(=78\pi +\frac{50\pi }{3}=94\tfrac{2}{3}\pi \)
Question
A curve has equation \(y=\frac{8}{x}+2x\)
(i) Find \(\frac{\mathrm{d} y}{\mathrm{d} x}\) and \(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}\).
(ii) Find the coordinates of the stationary points and state, with a reason, the nature of each stationary point.
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{8}{x^{2}}+2\)
\(\frac{\mathrm{d}^{2} y}{\mathrm{d} x^{2}}=\frac{16}{x^{3}}\)
(ii)\(-\frac{8}{x^{2}}+2=0\rightarrow 2x^{2}-8=0\)
\(x=\pm 2\)
\(y=\pm 8\)
\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}> 0\) when x=2 hence MiNIMUM
\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}<0\) when x=-2 MAXIMUM
Question
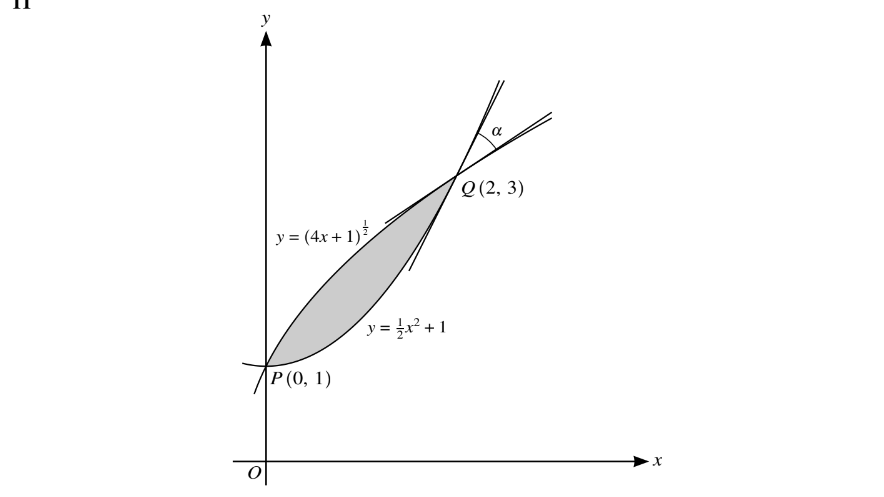
The diagram shows parts of the curves \(y=(4x+1)^{\frac{1}{2}}\) and \(y=\frac{1}{2}x^{2}+1\) intersecting at points P (0, 1) and Q( 2, 3). The angle between the tangents to the two curves at Q is \(\alpha \).
(i) Find \(\alpha \), giving your answer in degrees correct to 3 significant figures.
(ii) Find by integration the area of the shaded region.
Answer/Explanation
(i)For \(y=\left ( 4x+1 \right )^{\frac{1}{2}}\) ,
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\left [ \frac{1}{2}\left ( 4x+1 \right ) ^{-\frac{1}{2}}\right ]\times 4\)
When x=2,gradient \(m_{1}=\frac{2}{3}\)
For \(y=\frac{1}{2}x^{2}+1\),\(\frac{\mathrm{d} y}{\mathrm{d} x}=x\) → gradient \( m_{2}=2\)
\(\alpha =\tan ^{-1}m_{2}-\tan ^{-1}m_{1}\)
\(\alpha =63.43-33.69=29.7\)
Question
The function f is defined for x > 0 and is such that \( f{}’\left ( x \right )=2x-\frac{2}{x^{2}}\). The curve y = f(x) passes through the point P(2, 6.)
(i) Find the equation of the normal to the curve at P.
(ii) Find the equation of the curve.
(iii) Find the x-coordinate of the stationary point and state with a reason whether this point is a maximum or a minimum.
Answer/Explanation
(i)\(f{}'(2)=4-\frac{1}{2}=\frac{7}{2}\rightarrow \)gradient of normal =\(-\frac{2}{7}\)
\(y-6=-\frac{2}{7}(x-2)\)
(ii)\(f(x)=x^{2}+\frac{2}{x}+c\)
6=4+1+c⇒c=1
(iii)\(2x-\frac{2}{x^{2}}=0\)⇒\(2x^{3}-2=0\)
x=1
\(f{}”(x)=2+\frac{4}{x^{3}}\) or any valid method
\(f{}”(1)=6\) >0 hence minimum\)
Question.
The horizontal base of a solid prism is an equilateral triangle of side x cm. The sides of the prism are vertical. The height of the prism is h cm and the volume of the prism is \(2000 cm^3\).
(i) Express h in terms of x and show that the total surface area of the prism, \(Acm^2\) , is given by
\(A=\frac{\sqrt3}{2}x^2+\frac{24000}{\sqrt3}x^{-1}\).
(ii) Given that x can vary, find the value of x for which A has a stationary value.
(iii) Determine, showing all necessary working, the nature of this stationary value.
Answer/Explanation
(i)\(Volume=\left ( \frac{1}{2} \right )x^{2}\frac{\sqrt{3}}{2}h=2000\rightarrow h=\frac{8000}{\sqrt{3}x^{2}}\)\
\(A=3xh+(2)\times \frac{1}{2}\times x^{2}\times \frac{\sqrt{3}}{2}\)
Sub for \(h\rightarrow A=\frac{\sqrt{3}}{2}x^{2}+\frac{24000}{^{\sqrt{3}}}x^{-1}\)
(ii)\(\frac{\mathrm{d} A}{\mathrm{d} x}=\frac{\sqrt{3}}{2}2x-\frac{24000}{\sqrt{3}}x^{-2}\)
=0 when\( x^{3}=8000\rightarrow x=20\)
(iii)\(\frac{\mathrm{d} ^{2}A}{\mathrm{d} x^{2}}=\frac{\sqrt{3}}{2}2+\frac{48000}{\sqrt{3}}x^{-3}> 0\)
→Minimum
Question
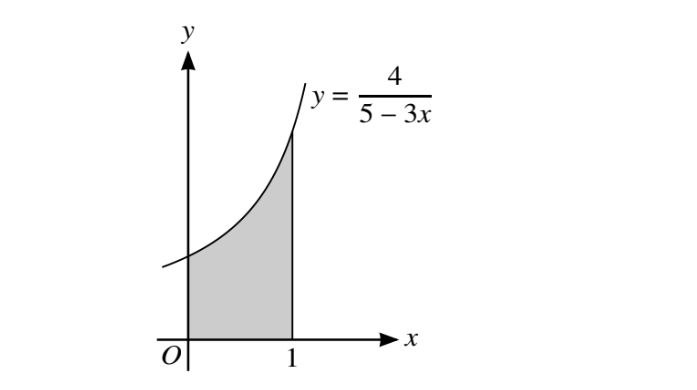
The diagram shows the part of the curve \(y=\frac{4}{5-3x}\)
(i)Find the equation of the normal to the curve at the curve at the point where x=1 in th e form y=mx+c,where m and c are constants.
The shaded region is bounded by the curve,the coordinate axes and the line x=1
(ii)Find, showing all the necessary w2orking,the volume obtained when this shaded region is rotated through \(360^{\circ}\) about the axis
Answer/Explanation
.(i) \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{4}{\left ( 5-3x \right )^{2}}\times \left ( -3 \right )\)
Gradient of tangent=3,Gradient of normal\(=\frac{1}{3}\)
→eqn:\(y-2=-\frac{1}{3}\left ( x-1 \right )\)
→\(y=-\frac{1}{3}x+\frac{7}{3}\)
(ii)Vol\(=\pi \int_{0}^{1}\frac{16}{\left ( 5-3x \right )^{2}}dx\)
\(\pi \left [ \frac{-16}{\left ( 5-3x \right )}\div -3 \right ]\)
\(\left ( \pi \left ( \frac{16}{6}-\frac{16}{15} \right ) \right )=\frac{8\pi }{5}\) (if limits switched must show – to +)
Question.
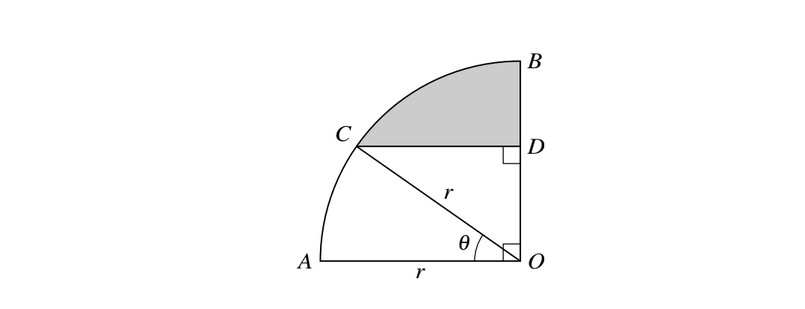
In the diagram, AOB is a quarter circle with centre O and radius r. The point C lies on the arc AB and the point D lies on OB. The line CD is parallel to AO and angle \(AOC = \Theta \)radians.
(i) Express the perimeter of the shaded region in terms of r,\(\Theta \)and \(\Pi\).
(ii) For the case where r = 5 cm and \(\Theta = 0.6\), find the area of the shaded region.
Answer/Explanation
(i) \(CD=r\cos \Theta ,BD=r-r\sin \Theta\)oe
\(Arc CB=r\left ( \frac{1}{2}\pi -\Theta \right )oe\)
\(\rightarrow P=r\cos \Theta +r-r\sin \Theta +r\left ( \frac{1}{2}\pi -\Theta \right )oe\)
(ii) Sector \(=\frac{1}{2}.5^{2}.\left ( \frac{1}{2} \pi -0.6\right )\)
Triangle\(=\frac{1}{2}.5\cos 0.6.5\sin 0.6\)
→Area=6.31
(or \(\frac{1}{4}\)circle-traingle-sector)
Question.
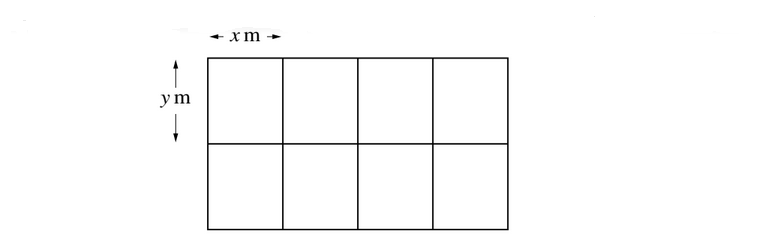
A farmer divides a rectangular piece of land into 8 equal-sized rectangular sheep pens as shown in the diagram. Each sheep pen measures x m by y m and is fully enclosed by metal fencing. The farmer uses 480 m of fencing.
(i) Show that the total area of land used for the sheep pens, \(A m^2\), is given by
\(A = 384x –9.6x^2.\)
(ii) Given that x and y can vary, find the dimensions of each sheep pen for which the value of A is a maximum. (There is no need to verify that the value of A is a maximum.)
Answer/Explanation
i) \(A=2y\times 4x\left ( =8xy \right )\)
10y+12x=480
\(\rightarrow A=384x-9.6x^{2}\)
(ii)\( \frac{\mathrm{d} A}{\mathrm{d} x}=384-19.2x\)
=0 when x=20
\(\rightarrow x=20,y=24\)
Uses \(x=-\frac{b}{2a}=\frac{-384}{-19.2}=20\),M1,A1
y=24,A1
From graph ,B1 for x=20,M1,A1 for y =24
Question.
A curve is such that \(\frac{\partial y}{\partial x}==2-8(3x+4)^\frac{1}{2}\)
(i) A point P moves along the curve in such a way that the x-coordinate is increasing at a constant rate of 0.3 units per second.
Find the rate of change of the y-coordinate as P crosses the y-axis.
The curve intersects the y-axis where y =\frac{4}{3}
(ii) Find the equation of the curve.
Answer/Explanation
(i) \(\frac{\mathrm{d} y}{\mathrm{d} x}=2-8\left ( 3x+4 \right )^{-\frac{1}{2}}\)
\(\left ( x=0,\rightarrow \frac{\mathrm{d} y}{\mathrm{d} x} =-2\right )\)
\(\frac{\mathrm{d} y}{\mathrm{d} t}=\frac{\mathrm{d} y}{\mathrm{d} x}\times \frac{\mathrm{d} x}{\mathrm{d} t}\rightarrow -0.6\)
(ii) \(y=\left \{ 2x \right \}\left \{ -\frac{8\sqrt{3x+4}}{\frac{1}{2}}\div 3 \right \}\left ( +c \right )\)
\(x=0,y=\frac{4}{3}\rightarrow c=12\)
Question.
The point A(2, 2) lies on the curve \(y = x^2 − 2x + 2\).
(i) Find the equation of the tangent to the curve at A.
The normal to the curve at A intersects the curve again at B.
(ii) Find the coordinates of B.
The tangents at A and B intersect each other at C.
(iii) Find the coordinates of C.
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=2x-2\) At x=2,m=2
Equation of tangent is \(y-2=2\left ( x-2 \right )\)
(ii) Equation of normal \(y-2=-\frac{1}{2}\left ( x-2 \right )\)
\(x^{2}-2x+2=-\frac{1}{2}x+3\rightarrow 2x^{2}-3x-2=0\)
\(x=-\frac{1}{2},y=\3frac{1}{4}\)
(iii) At \(x=-\frac{1}{2}\) ,grad=\(2\left ( -\frac{1}{2} \right )-2=-3\left ( x+\frac{1}{2} \right )\)
\(2x-2=-3x+\frac{7}{4}\)
\(x=\frac{3}{4},y=-\frac{1}{2}\)
Question.
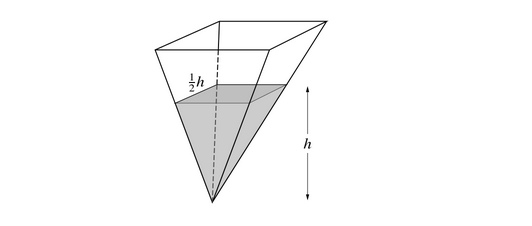
The diagram shows a water container in the form of an inverted pyramid, which is such that when the height of the water level is h cm the surface of the water is a square of side \(\frac{h}{2}\) cm.
(i) Express the volume of water in the container in terms of h.
[The volume of a pyramid having a base area A and vertical height is \( \frac{1}{3}Ah\).]
Water is steadily dripping into the container at a constant rate of \(20 cm^3\) per minute.
(ii) Find the rate, in cm per minute, at which the water level is rising when the height of the water level is 10 cm.
Answer/Explanation
(i) \(V=\frac{1}{12}h^{3}oe \)
(ii) \(\frac{\mathrm{d} V}{\mathrm{d} h}=\frac{1}{4}h^{2} \) or \( \frac{\mathrm{d} h}{\mathrm{d} V}=4\left ( 12v\right )^{-\frac{2}{3}}\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=\frac{\mathrm{d} h}{\mathrm{d} V}\times \frac{\mathrm{d} V}{\mathrm{d} t}=\frac{4}{h^{2}}\times 20\)
\(\left ( \frac{\mathrm{d} h}{\mathrm{d} t} \right )=\frac{4}{10^{2}}\times 20=0.8\) or equivalent fraction .
Question.
A vacuum flask (for keeping drinks hot) is modelled as a closed cylinder in which the internal radius is r cm and the internal height is h cm. The volume of the flask is 1000 cm. A flask is most efficient when the total internal surface area, A \(cm^2\), is a minimum.
(i) Show that \(A =2\Pi r^2+\frac{2000}{r}\).
(ii) Given that r can vary, find the value of r, correct to 1 decimal place, for which A has a stationary value and verify that the flask is most efficient when r takes this value.
Answer/Explanation
Ans:(i) A=2\Pi r(r+h)
\(\Pi r^2 h=1000\rightarrow h=\frac{1000}{\Pi r^{2}}\)
substitute hor h into \(A\rightarrow 2\Pi r^2+\frac{2000}{r}\)
(ii)

Question
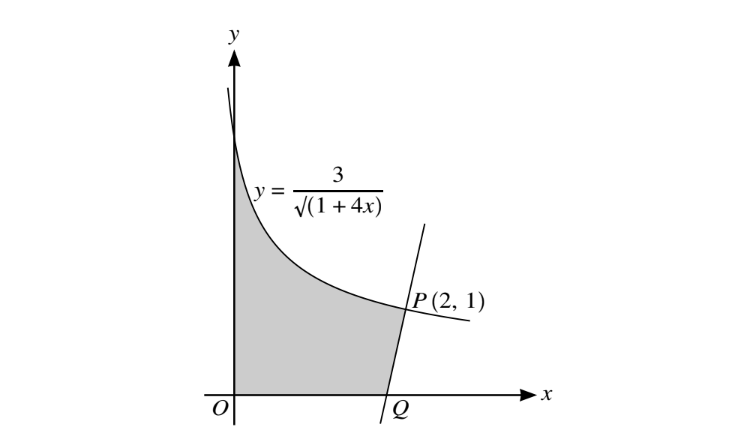
The diagram shows part of the curve\( y = \frac{3}{\sqrt({1+4x})} \) and a point P (2, 1) lying on the curve. The normal to the curve at P intersects the x-axis at Q.
(i) Show that the x-coordinate of Q is \(\frac{16}{9}\)
(ii) Find, showing all necessary working, the area of the shaded region.
Answer/Explanation

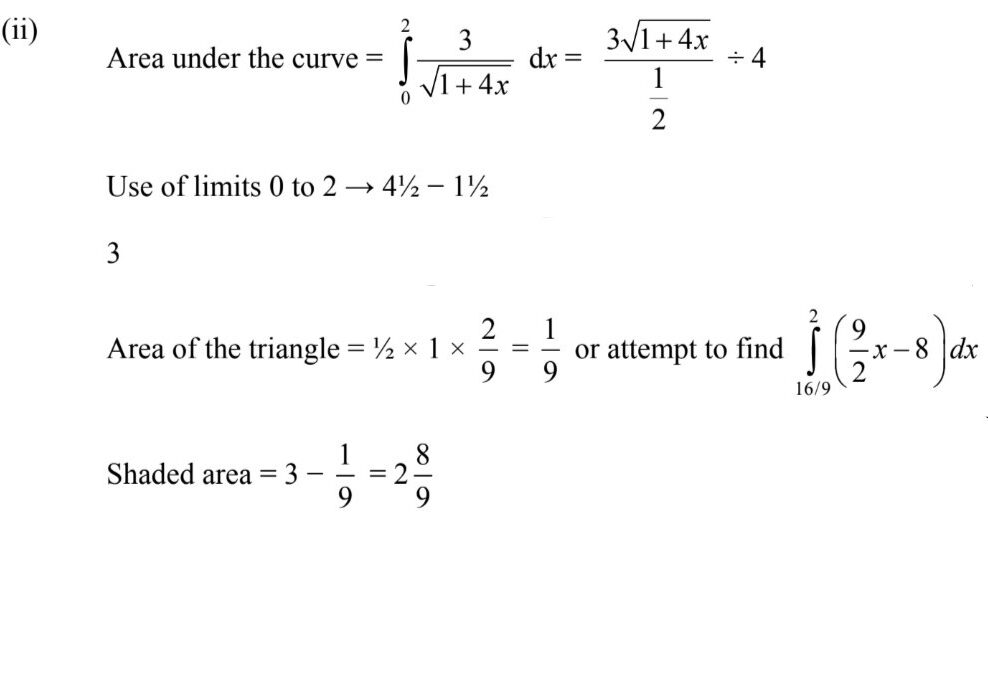
Question
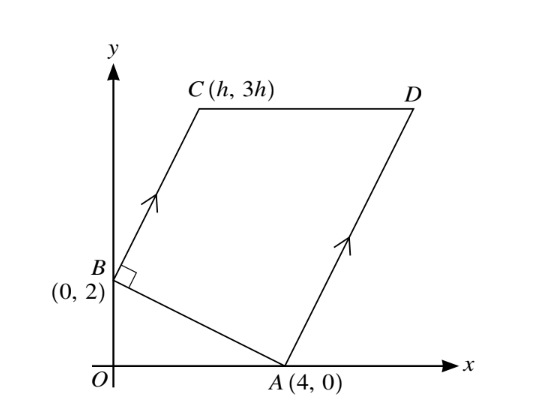
The diagram shows a trapezium ABCD in which the coordinates of A, B and C are 4, 0, 0, 2 and h, 3h respectively. The lines BC and AD are parallel, angle ABC = 90Å and CD is parallel to the x-axis.
(i) Find, by calculation, the value of h.
(ii) Hence find the coordinates of D.
Answer/Explanation
(i) Gradient of AB =−1⁄2→ Gradient of BC = 2
Forms equation in h \(\frac{3h-2}{h}\)=2 h = 2
Alternative method for question (i)
Vectors AB.BC=0 Solving h= 2
Alternative method for question (i)
Use of Pythagoras to find 3 lengths Solving h = 2
(ii) y coordinate of
D is 6, (3× ‘their’ h)
\(\frac{6-0}{x-4}=\rightarrow 7\rightarrow d(7,6)\) Vectors: AD.AB=0
Question
The line 4y = x + c, where c is a constant, is a tangent to the curve \(y^{2}=x+3\)
(i) Find the value of c.
(ii) Find the coordinates of P.
Answer/Explanation
(i) Eliminates x or y→\(y^{2}-4y+c-3=0
or x^{2}+(2c-16)x+c^{2}-48=0
uses b^{2}= 4ac\rightarrow 4c-28=0\) c=7
Alternative method for question 2(i)\( \frac{dy}{dx}=\frac{1}{\sqrt[2]{(x+3)}}=\frac{1}{4}\)
Solving c = 7
(ii) Uses c = 7,\(y^{2}\)− 4y + 4 = 0 (1, 2)
Question
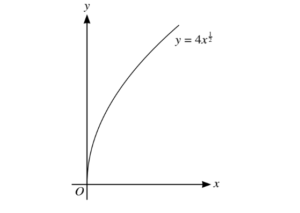
The diagram shows the curve with equation \(y = 4x^{\frac{1}{2}}\)
(i) The straight line with equation \(y = x + 3\) intersects the curve at points A and B. Find the length
of AB.
(ii) The tangent to the curve at a point T is parallel to AB. Find the coordinates of T.
(iii) Find the coordinates of the point of intersection of the normal to the curve at T with the line AB.
Answer/Explanation
10(i)
\(4x^{\frac{1}{2}}=x+3\rightarrow (x^{\frac{1}{2}})^{2}-4x^{\frac{1}{2}}+3=0\) OR \(16x=x^{2}+6x+9\)
\(x^{\frac{1}{2}}=1\) or 3
\(x^{2}-10x+9(=0)\)x=1or 9
y=4 or 12
AB=\((9-1)^{2}+(12-4)^{2}\)
AB=\(\sqrt{128} or8\sqrt{2} oe or 11.3\)
10(ii)
\(\frac{dy}{dx}=2x^{\frac{-1}{2}}\)
\(2x^{\frac{-1}{2}}=1\)
(4,8)
10(iii)
Equation of normal is y \(-8=-1(x-4)\)
Eliminate \(y(or x)\rightarrow -x+12=x+3 or y-3=12-y\)
\((4^{\frac{1}{2}},7^{\frac{1}{2}})\)
Question
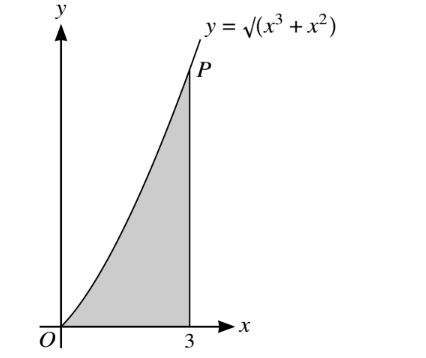
The diagram shows part of the curve with equation \(y=\sqrt{x^{3}+x^{2}}\) The shaded region is bounded by the curve, the x- axis and the line x = 3.
(i) Find, showing all necessary working, the volume obtained when the shaded region is rotated
through 360Å about the x-axis.
(ii) P is the point on the curve with x-coordinate 3. Find the y-coordinate of the point where the
normal to the curve at P crosses the y-axis.
Answer/Explanation
9(i)
\(V=(\Pi)\int (x^{3}+x^{2})(dx)\)
\(=(\Pi )\left [ \frac{x^{4}}{4} +\frac{x^{3}}{3}\right ]_{0}^{3}\)
\(=\Pi \left [ \frac{81}{4}+9 -(0) \right ]\)
\(=\frac{117\Pi }{4}\)
9(ii)
\(\frac{dy}{dx}=\frac{1}{2}(x^{3}+x^{2})\times (3x^{2^{}+}2x)\)
At (x = 3,y = 6)
At \(x=3,m=\frac{1}{2}\times \frac{1}{6}\pm \times 33=\frac{11}{4}\)
Equation of normal is
\(y-6=-\frac{4}{11}(x-3)\)
When
x = 0, y =\(\frac{78}{11}\)
Queastion
(i) Express \(x^{2}-4x+7\) in the form\((x+a)^{2}+b.\)
The function f is defined by \(f(x) = x^{2} − 4x + 7 \) for x < k, where k is a constant.
(ii) State the largest value of k for which f is a decreasing function.
The value of k is now given to be 1.
(iii) Find an expression for \(f^{-1}(x ) \)and state the domain of \( f^{-1}(x) \)
(iv) The function g is defined by \(g(x )= \frac{2}{x-1} \)for x > 1. Find an expression for gof(x) and state the range of gof(x).
.
Answer/Explanation
(i)
\(\left [ (x-2^{2}) \right ]+\left [ 3 \right ]\)
(ii)
Largest k is 2 Accept \(k\leq 2\)
(iii)
\(y=(x-2^{2})+3\Rightarrow x-2=\left ( \pm \right )\sqrt{y-3}\)
\(\Rightarrow F^{-1}(x)=2-\sqrt{x-3}forx>4\)
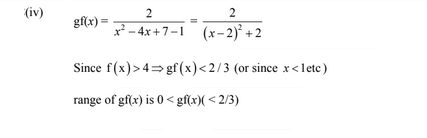
Question
A curve has equation \( y =(2x-1)^{-1}+2x\)
(i).Find \( \frac{\partial y}{\partial x}\) and \(\frac{\partial^2 y}{\partial x^2}\)
(ii) Find the x-coordinates of the stationary points and, showing all necessary working, determine
the nature of each stationary point.
Answer/Explanation
(i).\( \frac{\partial y}{\partial x}= -2(2x-1)^{-2}+2\)
\(\frac{\partial^2 y}{\partial x^2}=8(2x-1)^{-3}\)
(ii) Set \(\frac{\partial y}{\partial x}\) to zero and attempt to solve at least one correct step x = 0, 1
when x=0,\(\frac{\partial^2y}{\partial x^2}\)=-8(or<0),Hence MAX
when x=1,\(\frac{\partial^2y}{\partial x^2}\)=-8(or>0),Hence MIN
Question
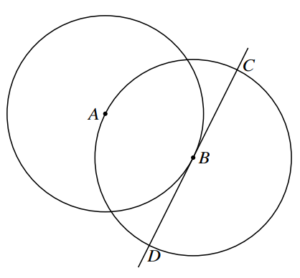
The diagram shows a circle with centre A passing through the point B. A second circle has centre B
and passes through A. The tangent at B to the first circle intersects the second circle at C and D.
The coordinates of A are (−1, 4) and the coordinates of B are (3, 2).
(a) Find the equation of the tangent CBD. [2]
(b) Find an equation of the circle with centre B. [3]
(c) Find, by calculation, the x-coordinates of C and D. [3]
Answer/Explanation
Ans
9 (a) \(m_{AB}=\frac{4-2}{-1-3}=-\frac{1}{2}\)
Equation of tangent is y – 2 = 2 (x – 3)
9 (b) \(AB^{2}=4^{2}+2^{2}=20\ or \ r^{2}=20\ or \ r=\sqrt{20}\ or \ AB=\sqrt{20}\)
Equation of circle centre B is \((x-3)^{2}+(y-2)^{2}=20\)
9 (c) \((x-3)^{2}+((2x-6)^{2}=their\ 20\)
\(5x^{2}-30x+25=0 \ or \ 5(x-3)^{2}=20\)
\(\left [ (5)(x-5)(x-1) \ or x-3=\pm 2 \right ]\ x=5, 1\)
Question
The equation of a curve is \(y=2+\sqrt{25-x^{2}}\).
Find the coordinates of the point on the curve at which the gradient is \(\frac{4}{3}\) [5]
Answer/Explanation
Ans
6 \(\frac{dy}{dx}=\left [ \frac{1}{2}(25-x^{2})^{-1/2} \right ]\times [-2x]\)
\(\frac{-x}{(25-x^{2})^{1/2}}=\frac{4}{3}\rightarrow \frac{x^{2}}{25-x^{2}}=\frac{16}{9}\)
\(16(25-x^{2})=9x^{2}\rightarrow 25x^{2}=400\rightarrow x=(\pm )4\)
When x = ‒ 4, y = 5 → ( ‒ 4, 5)
Question
Air is being pumped into a balloon in the shape of a sphere so that its volume is increasing at a constant
rate of 50 cm3 s−1.
Find the rate at which the radius of the balloon is increasing when the radius is 10 cm. [3]
Answer/Explanation
Ans
3 (Derivative =) 24 πr2 (→ 400π)
\(\frac{50}{their\ derivative}\)
\(\frac{1}{8\pi }\ or\ 0.0398\)
Question
A curve is such that \(\frac{dy}{dx}=\frac{6}{3x-2}^3\) and A (1, -3) lies on the curve. A point is moving along the curve and at A the y – coordinate of the point is increasing at 3 units per second.
(a) Find the rate of increase at A of the x-coordinate of the point.
(b) Find the equation of the curve.
Answer/Explanation
Ans:
(a) At \(x=1,\frac{dy}{dx}=6\)
\(\frac{dx}{dt}=(\frac{dx}{dy}\times \frac{dy}{dt})=\frac{1}{6}\times 3=\frac{1}{2}\)
(b) \([y=](\frac{6(3x-2)^{-2}}{-2})+(3)[+c]\)
-3=-1+c
\(y=-(3x-2)^{-2}-2\)
Question
The equation of a curve is y = (2k − 3)x2 − kx − (k − 2), where k is a constant. The line y = 3x − 4 is a
tangent to the curve.
Find the value of k [5]
Answer/Explanation
Ans
6 \((2k-3)x^{2}-kx-(k-2)=3x-4\)
\((2k-3)x^{2}-(k+3)x-(k-6)[=0]\)
\((k+3)^{2}+4(2k-3)(k-6)[=0]\)
9k2 −54k + 81[=0] [leading to k2 – 6k + 9=0 ]
k = 3
Alternative method for Question 6
\( (2k-3)x^{2}-kx-(k-2)=3x-4\)
\(2(2k-3)x-k=3\Rightarrow x=\frac{k+3}{4k-6}\ or \ k=\frac{3+6x}{4x-1}\)
either \( (2k-3)\left ( \frac{k+3}{4k-6} \right )^{2}-k\left ( \frac{k+3}{4k-6} \right )-(k-2)=3\left ( \frac{k+3}{4k-6} \right )-4\)
or \(4x\left ( \frac{3x^{2}+3x-6}{2x^{2}-x-1} \right )-6x-\left ( \frac{3x^{2}+3x-6}{2x^{2}-x-1} \right )=3\)
9k2 – 54 + 81 [=0] [leading to k2 – 6k + 9 = 0] \( k = 3 \)
Question
The equation of a curve is \(y=2\sqrt{3x+4}-x\)
(a) Find the equation of the normal to the curve at the point (4, 4), giving your answer in the form
y = mx + c. [5]
(b) Find the coordinates of the stationary point. [3]
(c) Determine the nature of the stationary point. [2]
(d) Find the exact area of the region bounded by the curve, the x-axis and the lines x = 0 and x = 4. [4]
Answer/Explanation
Ans
11 (a) \(\frac{dx}{dy}=3(3x+4)^{-0.5}-1\)
Gradient of tangent \(=-\frac{1}{4}\) and Gradient of normal = 4
Equation of line is (y – 4) = 4(x – 4) or evaluate c
So y = 4x – 12
11 (b) 3(3x+4)-0.5 -1 = 0
Solving as far as x=
\(x=\frac{5}{3}, y=2\left ( 3\times \frac{5}{3}+4 \right )^{0.5}-\frac{5}{3}=\frac{13}{3}\)
At \(x=\frac{5}{3} \frac{d^{2}y}{dx^{2}}\) is negative so the point is a maximum
11 (d) \(Area-[f2(3x+4)^{0.5}-xdx=]\frac{4}{9}(3x+4)^{1.5}-\frac{1}{2}x^{2}\)
\(\left ( \frac{4}{9}(16)^{1.5}-\frac{1}{2}(4)^{2} \right )-\frac{4}{9}(4)^{1.5}=\frac{256}{9}-8-\frac{32}{9}\)
\(16\frac{8}{9}\)