Question
A curve is such that \(\frac{\mathrm{d} y}{\mathrm{d} x}=x^{\frac{1}{2}}-x^{-\frac{1}{2}}\) .The curve passes through the point \(\left ( 4,\frac{2}{3} \right )\)
(i)Find the equation of the curve .
(ii)Find \(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}\)
(iii)Find the coordinates of the stationary point and determine its nature.
▶️Answer/Explanation
(i) Given the derivative \( \frac{dy}{dx} = x^{\frac{1}{2}} – x^{-\frac{1}{2}} \), we need to integrate this to find the equation of the curve.
\( \frac{dy}{dx} = x^{\frac{1}{2}} – x^{-\frac{1}{2}} \)
\( dy = \left( x^{\frac{1}{2}} – x^{-\frac{1}{2}} \right) dx \)
\( y = \int \left( x^{\frac{1}{2}} – x^{-\frac{1}{2}} \right) dx \)
\( y = \int x^{\frac{1}{2}} dx – \int x^{-\frac{1}{2}} dx \)
\( y = \frac{2}{3}x^{\frac{3}{2}} – 2x^{\frac{1}{2}} + C \)
To find the constant of integration \( C \), we use the point \( (4, \frac{2}{3}) \) through which the curve passes:
\( \frac{2}{3} = \frac{2}{3}(4)^{\frac{3}{2}} – 2(4)^{\frac{1}{2}} + C \)
\( \frac{2}{3} = \frac{2}{3} \cdot 8 – 2 \cdot 2 + C \)
\( \frac{2}{3} = \frac{16}{3} – 4 + C \)
\( C = \frac{2}{3} – \frac{16}{3} + 4 \)
\( C = -\frac{14}{3} + 4 \)
\( C = -\frac{14}{3} + \frac{12}{3} \)
\( C = -\frac{2}{3} \)
So, the equation of the curve is \( y = \frac{2}{3}x^{\frac{3}{2}} – 2x^{\frac{1}{2}} – \frac{2}{3} \).
(ii) To find the second derivative, we differentiate the first derivative:
\( \frac{d^2y}{dx^2} = \frac{d}{dx} \left( x^{\frac{1}{2}} – x^{-\frac{1}{2}} \right) \)
\( \frac{d^2y}{dx^2} = \frac{1}{2}x^{-\frac{1}{2}} + \frac{1}{2}x^{-\frac{3}{2}}\)
(iii) A stationary point occurs where \( \frac{dy}{dx} = 0 \). So we set the first derivative to zero and solve for \( x \):
\( x^{\frac{1}{2}} – x^{-\frac{1}{2}} = 0 \)
\( x^{\frac{1}{2}} = x^{-\frac{1}{2}} \)
\( x = 1 \)
Now, substitute \( x = 1 \) into the equation of the curve to find \( y \):
\( y = \frac{2}{3}(1)^{\frac{3}{2}} – 2(1)^{\frac{1}{2}} – \frac{2}{3} \)
\( y = \frac{2}{3} – 2 – \frac{2}{3} \)
\(y = -2 \)
So, the stationary point is at \( (1, -2) \).
To determine the nature of the stationary point, we check the sign of \( \frac{d^2y}{dx^2} \) at \( x = 1 \):
\( \frac{d^2y}{dx^2}|_{x=1} = \frac{1}{2}(1)^{-\frac{1}{2}} + \frac{1}{2}(1)^{-\frac{3}{2}} \)
\( \frac{d^2y}{dx^2}|_{x=1} = \frac{1}{2} + \frac{1}{2} \)
\( \frac{d^2y}{dx^2}|_{x=1} = 1 \)
Since \( \frac{d^2y}{dx^2}|_{x=1} > 0 \), the stationary point at \( (1, -2) \) is a local minimum.
Question
A curve has equation \(y=\frac{8}{x}+2x\)
(i) Find \(\frac{\mathrm{d} y}{\mathrm{d} x}\) and \(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}\).
(ii) Find the coordinates of the stationary points and state, with a reason, the nature of each stationary point.
▶️Answer/Explanation
(i)The equation of the curve \( y = \frac{8}{x} + 2x \),
First Derivative \(\frac{dy}{dx}\):
\( \frac{dy}{dx} = \frac{d}{dx}\left(\frac{8}{x}\right) + \frac{d}{dx}(2x) \)
\( \frac{dy}{dx} = -\frac{8}{x^2} + 2 \)
Second Derivative \(\frac{d^2y}{dx^2}\):
\( \frac{d^2y}{dx^2} = \frac{d}{dx}\left(-\frac{8}{x^2} + 2\right) \)
\( \frac{d^2y}{dx^2} = \frac{d}{dx}\left(-\frac{8}{x^2}\right) \)
\( \frac{d^2y}{dx^2} = 16x^{-3} \)
(ii) Stationary points occur where \(\frac{dy}{dx} = 0\). We set the first derivative to zero and solve for \(x\):
\( -\frac{8}{x^2} + 2 = 0 \)
\( 2 = \frac{8}{x^2} \)
\( x^2 = \frac{8}{2} \)
\( x^2 = 4 \)
\( x = \pm 2 \)
We substitute these values into the original equation to find the corresponding \(y\) values:
For \(x = 2\):
\( y = \frac{8}{2} + 2 \cdot 2 \)
\( y = 4 + 4 \)
\( y = 8 \)
For \(x = -2\):
\( y = \frac{8}{-2} + 2 \cdot (-2) \)
\( y = -4 – 4 \)
\( y = -8 \)
So, the coordinates of the stationary points are \((2, 8)\) and \((-2, -8)\).
To determine the nature of these stationary points, we check the sign of \(\frac{d^2y}{dx^2}\) at these points:
For \(x = 2\):
\( \frac{d^2y}{dx^2}|_{x=2} = 16(2)^{-3} \)
\( \frac{d^2y}{dx^2}|_{x=2} = 16 \cdot \frac{1}{8} \)
\( \frac{d^2y}{dx^2}|_{x=2} = 2 \)
Since \(\frac{d^2y}{dx^2}|_{x=2} > 0\), the stationary point at \((2, 8)\) is a local minimum.
For \(x = -2\):
\( \frac{d^2y}{dx^2}|_{x=-2} = 16(-2)^{-3} \)
\( \frac{d^2y}{dx^2}|_{x=-2} = 16 \cdot \frac{-1}{8} \)
\( \frac{d^2y}{dx^2}|_{x=-2} = -2 \)
Since \(\frac{d^2y}{dx^2}|_{x=-2} < 0\), the stationary point at \((-2, -8)\) is a local maximum.
Question
The function f is defined for x≥ 0 by \(f(x) =(4x + 1)^\frac{3}{2}\).
(i) Find f′(x) and f′′(x).
The first, second and third terms of a geometric progression are respectively f(2), f′(2) and kf′′(2).
(ii) Find the value of the constant k.
▶️Answer/Explanation
(i) \( f(x) = (4x + 1)^{\frac{3}{2}} \)
To find the first derivative, we use the chain rule:
\( f'(x) = \frac{d}{dx} \left( (4x + 1)^{\frac{3}{2}} \right) \)
\( f'(x) = \frac{3}{2} \cdot (4x + 1)^{\frac{1}{2}} \cdot \frac{d}{dx}(4x + 1) \)
\( f'(x) = \frac{3}{2} \cdot (4x + 1)^{\frac{1}{2}} \cdot 4 \)
\( f'(x) = 6(4x + 1)^{\frac{1}{2}}\)
2.\( f”(x) = \frac{d}{dx} \left( 6(4x + 1)^{\frac{1}{2}} \right) \)
\( f”(x) = 6 \cdot \frac{1}{2} \cdot (4x + 1)^{-\frac{1}{2}} \cdot \frac{d}{dx}(4x + 1) \)
\(f”(x) = 3(4x + 1)^{-\frac{1}{2}} \cdot 4 \)
\( f”(x) = 12(4x + 1)^{-\frac{1}{2}} \)
(ii) Given that the first, second, and third terms of a geometric progression are \( f(2) \), \( f'(2) \), and \( k \cdot f”(2) \) respectively, we can find \( k \) by using the property of a geometric progression where the square of any term (except the first and last) is equal to the product of its adjacent terms. Thus,
\( [f'(2)]^2 = f(2) \cdot k \cdot f”(2) \]
\( f(2) = (4 \cdot 2 + 1)^{\frac{3}{2}} = (9)^{\frac{3}{2}} \)
\( f'(2) = 6(4 \cdot 2 + 1)^{\frac{1}{2}} = 6(9)^{\frac{1}{2}} = 18 \)
\( f”(2) = 12(4 \cdot 2 + 1)^{-\frac{1}{2}} = 12(9)^{-\frac{1}{2}} = \frac{12}{3} = 4 \)
Now, substituting these values into the equation:
\( (18)^2 = 9^{\frac{3}{2}} \cdot k \cdot 4 \)
\( 324 = 27 \cdot k \cdot 4 \)
\( 324 = 108k \)
\( k = \frac{324}{108} \)
\( k = 3 \)
Hence, the value of the constant \( k \) is 3.
Question
The function f is defined by f(x) = 2 − 3 cos x for 0 ≤ x ≤ 20.
(i) State the range of f.
(ii) Sketch the graph of y=f(x).
The function g is defined by g(x)= 2 − 3 cos x for 0 ≤ x ≤ p, where p is a constant.
(iii) State the largest value of p for which g has an inverse.
(iv) For this value of p, find an expression for \(g^{-1}(x)\)
▶️Answer/Explanation
(i) The function \( f(x) = 2 – 3 \cos x \) is a transformation of the basic cosine function. The cosine function, \( \cos x \), varies between -1 and 1. Therefore, \( -3 \cos x \) will vary between -3 and 3 because multiplying by -3 reverses the direction of the cosine wave and stretches it to three times its original amplitude.
When \( \cos x = 1 \), \( f(x) = 2 – 3(1) = -1 \).
When \( \cos x = -1 \), \( f(x) = 2 – 3(-1) = 2 + 3 = 5 \).
So the range of \( f \) is from -1 to 5.
(ii) To sketch the graph, consider these key points:
The function is a cosine wave starting from \( x = 0 \) to \( x = 20 \).
It is shifted upwards by 2 units and has an amplitude of 3.
The period of a cosine function is \( 2\pi \), but we’re only interested in the portion from 0 to 20.
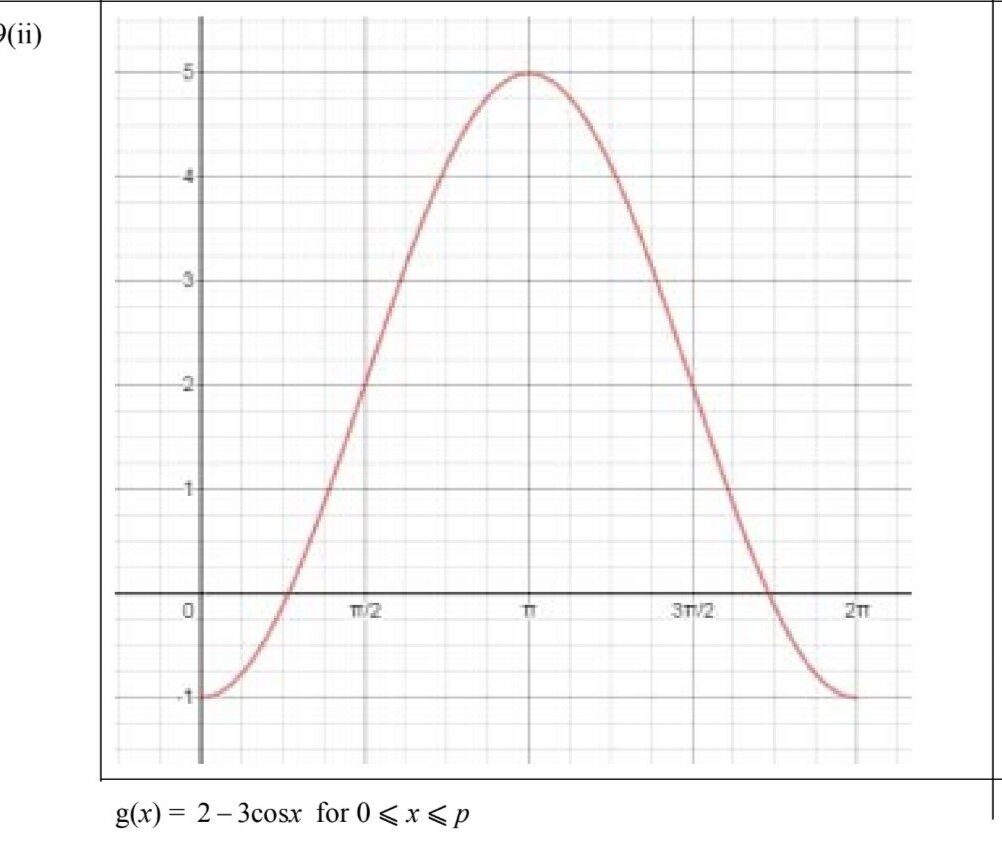
The graph will show a wavy line, starting at \( f(0) = 2 – 3 \cos 0 = -1 \) and oscillating between -1 and 5 with peaks and troughs corresponding to the cosine function.
(iii) For a function to have an inverse, it must be one-to-one (bijective) on its domain. A cosine function has a period of \( 2\pi \), but to maintain the one-to-one property, we must restrict the domain to half of its period, which is \( \pi \). Therefore, the largest value of \( p \) for which \( g \) has an inverse is \( \pi \).
(iv) To find the inverse of \( g(x) = 2 – 3 \cos x \) on the restricted domain \( 0 \leq x \leq \pi \),
Swap \( x \) and \( y \): \( x = 2 – 3 \cos y \).
Solve for \( y \):
\( \begin{align*}
x &= 2 – 3 \cos y \\
\cos y &= \frac{2 – x}{3} \\
y &= \cos^{-1}\left(\frac{2 – x}{3}\right).
\end{align*} \)
So, the inverse function \( g^{-1}(x) \) is \( g^{-1}(x) = \cos^{-1}\left(\frac{2 – x}{3}\right) \).
Question
A curve has equation \( y =(2x-1)^{-1}+2x\)
(i).Find \( \frac{\partial y}{\partial x}\) and \(\frac{\partial^2 y}{\partial x^2}\)
(ii) Find the x-coordinates of the stationary points and, showing all necessary working, determine
the nature of each stationary point.
▶️Answer/Explanation
(a)\( y = (3 – 2x)^3 + 24x \)
Differentiating \((3 – 2x)^3\)
Using the chain rule. If \( u = 3 – 2x \), then \(\frac{du}{dx} = -2\), and \(\frac{d}{dx}(u^3) = 3u^2\).
So, \(\frac{d}{dx}((3 – 2x)^3) = 3(3 – 2x)^2(-2)\).
Differentiate \(24x\)
So, \(\frac{\partial y}{\partial x} = -6(3 – 2x)^2 + 24\).
Second derivative \(\frac{\partial^2 y}{\partial x^2}\):
Differentiating \(-6(3 – 2x)^2 + 24\):
Differentiating \(-6(3 – 2x)^2\): Again using the chain rule, \(\frac{d}{dx}(-6(3 – 2x)^2) = -6(2)(3 – 2x)(-2)\).
The derivative of \(24\) is \(0\).
So, \(\frac{\partial^2 y}{\partial x^2} = 24(3 – 2x)\).
(b) Stationary points occur where \(\frac{\partial y}{\partial x} = 0\)
Set \(-6(3 – 2x)^2 + 24 = 0\):
\( \begin{align*}
-6(3 – 2x)^2 + 24 &= 0 \\
(3 – 2x)^2 &= 4 \\
3 – 2x &= \pm 2 \\
2x &= 3 \pm 2.
\end{align*} \)
So, we have two solutions:
\(2x = 3 + 2\), then \(x = \frac{5}{2}\).
\(2x = 3 – 2\), then \(x = \frac{1}{2}\).
For \(x = \frac{5}{2}\), \(y = (3 – 2(\frac{5}{2}))^3 + 24(\frac{5}{2}) = (3 – 5)^3 + 60 = (-2)^3 + 60 = -8 + 60 = 52\).
For \(x = \frac{1}{2}\), \(y = (3 – 2(\frac{1}{2}))^3 + 24(\frac{1}{2}) = (3 – 1)^3 + 12 = 2^3 + 12 = 8 + 12 = 20\).
Hence, the coordinates of the stationary points are \((\frac{5}{2}, 52)\) and \((\frac{1}{2}, 20)\).
Question
The equation of a curve is \(y =(3 − 2x)^{3} + 24x\).
(a) Find expressions for \(\frac{\partial y}{\partial x}\) and \(\frac{\partial^2 y}{\partial x^2}\).
(b) Find the coordinates of each of the stationary points on the curve.
▶️Answer/Explanation
(a) The first derivative of a function gives the rate at which the function’s value changes as \( x \) changes.
Differentiating \( (3 – 2x)^3 \):
Using the chain rule: If \( u = 3 – 2x \), then \( \frac{du}{dx} = -2 \), and \( \frac{d}{dx}(u^3) = 3u^2 \).
Therefore, \( \frac{d}{dx}((3 – 2x)^3) = 3(3 – 2x)^2 \cdot \frac{du}{dx} = 3(3 – 2x)^2 \cdot (-2) \).
The derivative of \( 24x \) with respect to \( x \) is \( 24 \).
\( \frac{dy}{dx} = -6(3 – 2x)^2 + 24 \)
(b) The second derivative of a function gives the rate of change of the rate of change, which is used to determine the concavity of the function. To find \(\frac{d^2y}{dx^2}\), we differentiate \(\frac{dy}{dx}\).
Differentiate \(-6(3 – 2x)^2\):
Again using the chain rule, we get \( \frac{d}{dx}(-6(3 – 2x)^2) = -6 \cdot 2(3 – 2x) \cdot (-2) \).
So, combining these, we get:
\( \frac{d^2y}{dx^2} = 24(3 – 2x) \)
(c) Stationary points occur where the first derivative \(\frac{dy}{dx}\) equals zero. This is because stationary points are points where the rate of change of the function is zero, meaning the function is neither increasing nor decreasing at these points.
\(\frac{dy}{dx} = 0\):
\( -6(3 – 2x)^2 + 24 = 0 \)
\( (3 – 2x)^2 = 4 \)
\( 3 – 2x = \pm 2 \)
\( 2x = 3 \pm 2 \)
For \(3 + 2\), we get \(2x = 5\) or \(x = \frac{5}{2}\).
For \(3 – 2\), we get \(2x = 1\) or \(x = \frac{1}{2}\).
For \(x = \frac{5}{2}\), \(y = (3 – 2 \times \frac{5}{2})^3 + 24 \times \frac{5}{2} = (-2)^3 + 60 = -8 + 60 = 52\).
For \(x = \frac{1}{2}\), \(y = (3 – 2 \times \frac{1}{2})^3 + 24 \times \frac{1}{2} = 2^3 + 12 = 8 + 12 = 20\).
For \(x = \frac{1}{2}\), \(\frac{d^2y}{dx^2} = 24(3 – 2 \times \frac{1}{2}) = 48\). Since this is positive, the curve is concave up at \(x = \frac{1}{2}\), indicating a minimum.
For \(x = \frac{5}{2}\), \(\frac{d^2y}{dx^2} = 24(3 – 2 \times \frac{5}{2}) = -48\). Since this is negative, the curve is concave down at \(x = \frac{5}{2}\), indicating a maximum.
Question
A curve has equation y = f(x), and it is given that f′ (x) \(= 2x^{2} – 7 – \frac{4}{x^{2}}\)
(a) Given that f(1) = \(-\frac{1}{3}\), find f(x).
(b) Find the coordinates of the stationary points on the curve.
(c) Find f′′ (x).
(d) Hence, or otherwise, determine the nature of each of the stationary points.
▶️Answer/Explanation
(a) Given the derivative \( f'(x) = 2x^2 – 7 – \frac{4}{x^2} \) and that \( f(1) = -\frac{1}{3} \), we need to integrate \( f'(x) \) to find \( f(x) \) and then use the given condition to find the constant of integration.
\( \int (2x^2 – 7 – \frac{4}{x^2}) dx \)
\( = \int 2x^2 dx – \int 7 dx – \int \frac{4}{x^2} dx \)
\( = \frac{2}{3}x^3 – 7x + 4x^{-1} + C \)
So, \( f(x) = \frac{2}{3}x^3 – 7x + 4x^{-1} + C \).
Using \( f(1) = -\frac{1}{3} \),
\( -\frac{1}{3} = \frac{2}{3}(1)^3 – 7(1) + 4(1)^{-1} + C \)
\( -\frac{1}{3} = \frac{2}{3} – 7 + 4 + C \)
\( C = -\frac{1}{3} – \frac{2}{3} + 7 – 4 \)
\( C = -1 \)
Therefore, \( f(x) = \frac{2}{3}x^3 – 7x + 4x^{-1} – 1 \).
(b) Stationary points occur where the derivative is zero, i.e., \( f'(x) = 0 \).
Solving \( f'(x) = 0 \)
\( 2x^2 – 7 – \frac{4}{x^2} = 0 \)
\( 2x^4 – 7x^2 – 4 = 0 \)
This is a quadratic in \( x^2 \). Let \( u = x^2 \), so the equation becomes:
\( 2u^2 – 7u – 4 = 0 \)
\( u = \frac{7 \pm \sqrt{(-7)^2 – 4 \cdot 2 \cdot (-4)}}{2 \cdot 2} \)
\( u = \frac{7 \pm \sqrt{49 + 32}}{4} \)
\( u = \frac{7 \pm \sqrt{81}}{4} \)
\( u = \frac{7 \pm 9}{4} \)
So, \( u = 4 \) or \( u = -\frac{1}{2} \) (discard as \( x^2 \) cannot be negative).
\( x^2 = 4 \) gives \( x = \pm 2 \).
Substitute \( x = 2 \) and \( x = -2 \) into \( f(x) \):
For \( x = 2 \), \( y = f(2) = \frac{2}{3}(2)^3 – 7(2) + 4(2)^{-1} – 1 \)=-7.667\)
For \( x = -2 \), \( y = f(-2) = \frac{2}{3}(-2)^3 – 7(-2) + 4(-2)^{-1} – 1 \)=5.667\)
(c) To find \( f”(x) \), differentiate \( f'(x) \):
\( f”(x) = \frac{d}{dx}(2x^2 – 7 – \frac{4}{x^2}) \)
\( = 4x + \frac{8}{x^3} \)
(d) The nature of a stationary point is determined by the second derivative.
If \( f”(x) > 0 \), the point is a minimum; if \( f”(x) < 0 \), the point is a maximum.
\( f”(2) = 4(2) + \frac{8}{2^3}=9 \)> 0 minimum
\( f”(-2) = 4(-2) + \frac{8}{(-2)^3}=-9 \)< 0 maximum