Question
The point P(3,5) lies on the curve \(y=\frac{1}{x-1}-\frac{9}{x-5}\)
(i)Find the x-coordinate of the point where the normal to the curve at P intersects the x-axis.
(ii)Find the x-coordinates of each of the stationary points on the curve and determine the nature of each stationary point,justifying your answer.
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=-(x-1)^{-2}+9(x-5)^{-2}\)
\(m_{tangent}=-\frac{1}{4}+\frac{9}{4}=2\)
\(Equation of normal is y-5=-\frac{1}{2}\left ( x-3 \right )\)
x=13
(ii)\(\left ( x-5 \right )^{2}=9\left ( x-1 \right )^{2}\)
\(x-5=\left ( \pm \right )3\left ( x-1 \right )\) or \(\left ( x^{2}-x-2 \right )=0\)
x=-1 or 2
\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=2\left ( x-1 \right )^{-3}-18\left ( x-5 \right )^{-3}\)
When x=-1,\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=-\frac{1}{6} < 0\) MAX
When x=2 \(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=\frac{8}{3} > 0\) MIN
Question.
The horizontal base of a solid prism is an equilateral triangle of side x cm. The sides of the prism are vertical. The height of the prism is h cm and the volume of the prism is \(2000 cm^3\).
(i) Express h in terms of x and show that the total surface area of the prism, \(Acm^2\) , is given by
\(A=\frac{\sqrt3}{2}x^2+\frac{24000}{\sqrt3}x^{-1}\).
(ii) Given that x can vary, find the value of x for which A has a stationary value.
(iii) Determine, showing all necessary working, the nature of this stationary value.
Answer/Explanation
(i)\(Volume=\left ( \frac{1}{2} \right )x^{2}\frac{\sqrt{3}}{2}h=2000\rightarrow h=\frac{8000}{\sqrt{3}x^{2}}\)\
\(A=3xh+(2)\times \frac{1}{2}\times x^{2}\times \frac{\sqrt{3}}{2}\)
Sub for \(h\rightarrow A=\frac{\sqrt{3}}{2}x^{2}+\frac{24000}{^{\sqrt{3}}}x^{-1}\)
(ii)\(\frac{\mathrm{d} A}{\mathrm{d} x}=\frac{\sqrt{3}}{2}2x-\frac{24000}{\sqrt{3}}x^{-2}\)
=0 when\( x^{3}=8000\rightarrow x=20\)
(iii)\(\frac{\mathrm{d} ^{2}A}{\mathrm{d} x^{2}}=\frac{\sqrt{3}}{2}2+\frac{48000}{\sqrt{3}}x^{-3}> 0\)
→Minimum
Question.
(a) Find the values of the constant m for which the line y = mx is a tangent to the curve \(y = 2x^2 – 4x + 8\).
(b) The function f is defined for x \in R by \(f(x) = x^2 + ax + b\), where a and b are constants. The
solutions of the equation f(x) = 0 are x = 1 and x = 9.
Find
(i) the values of a and b,
(ii) the coordinates of the vertex of the curve y = f(x).
Answer/Explanation
(i)\(y=2x^{2}-4x+8\)
Equates with y=mx and selects a,b,c
Uses \(b^{2}=4ac\)
\(\rightarrow a=-10,b=9\)
(iii) Calculus or \(x=\frac{1}{2}\left ( 1+9 \right )\) by symmetry
\(\rightarrow \left ( 5,-16 \right )\)
Question.
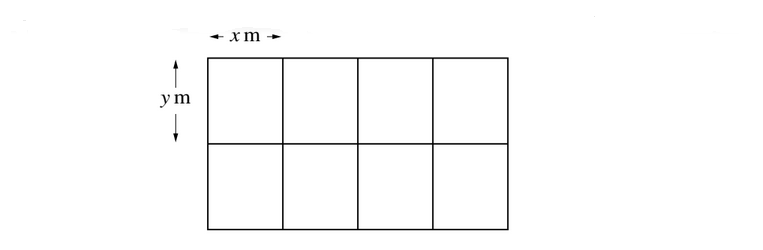
A farmer divides a rectangular piece of land into 8 equal-sized rectangular sheep pens as shown in the diagram. Each sheep pen measures x m by y m and is fully enclosed by metal fencing. The farmer uses 480 m of fencing.
(i) Show that the total area of land used for the sheep pens, \(A m^2\), is given by
\(A = 384x –9.6x^2.\)
(ii) Given that x and y can vary, find the dimensions of each sheep pen for which the value of A is a maximum. (There is no need to verify that the value of A is a maximum.)(
Answer/Explanation
i) \(A=2y\times 4x\left ( =8xy \right )\)
10y+12x=480
\(\rightarrow A=384x-9.6x^{2}\)
(ii)\( \frac{\mathrm{d} A}{\mathrm{d} x}=384-19.2x\)
=0 when x=20
\(\rightarrow x=20,y=24\)
Uses \(x=-\frac{b}{2a}=\frac{-384}{-19.2}=20\),M1,A1
y=24,A1
From graph ,B1 for x=20,M1,A1 for y =24
Question.
A vacuum flask (for keeping drinks hot) is modelled as a closed cylinder in which the internal radius is r cm and the internal height is h cm. The volume of the flask is 1000 cm. A flask is most efficient when the total internal surface area, A \(cm^2\), is a minimum.
(i) Show that \(A =2\Pi r^2+\frac{2000}{r}\).
(ii) Given that r can vary, find the value of r, correct to 1 decimal place, for which A has a stationary value and verify that the flask is most efficient when r takes this value.
Answer/Explanation
Ans:(i) A=2\Pi r(r+h)
\(\Pi r^2 h=1000\rightarrow h=\frac{1000}{\Pi r^{2}}\)
substitute hor h into \(A\rightarrow 2\Pi r^2+\frac{2000}{r}\)
(ii)

Question
The function f is defined by f(x) = 2 − 3 cos x for 0 ≤ x ≤ 20.
(i) State the range of f.
(ii) Sketch the graph of y=f(x).
The function g is defined by g(x)= 2 − 3 cos x for 0 ≤ x ≤ p, where p is a constant.
(iii) State the largest value of p for which g has an inverse.
(iv) For this value of p, find an expression for \(g^{-1}(x)\)
Answer/Explanation
(i)
−1 ⩽ f(x) ⩽ 5 or [–1, 5] (may use y or f instead of f(x))
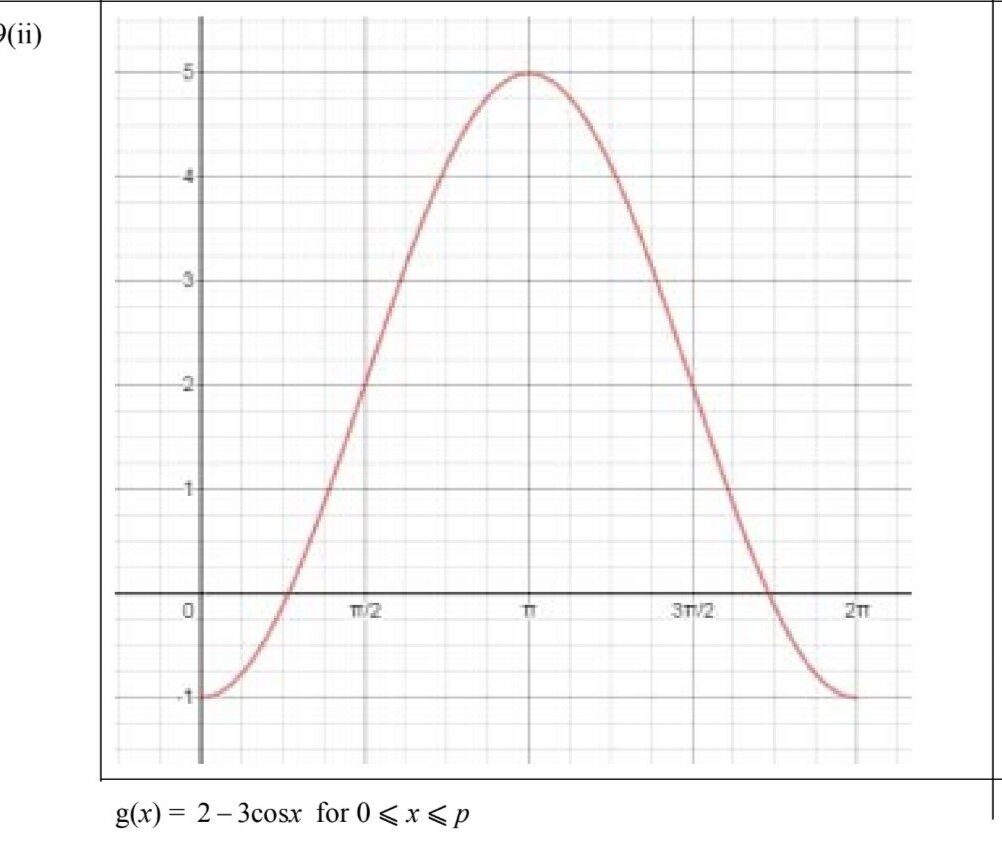
(iii) (greatest value of p =)π
9(iv)
\(x = 2− 3cosx → cosx =1⁄3(2-x)\)
\(g^{-1}=cos^{-1}\frac{2-x}{3}\)
Question
A curve has equation \(y=x^2-2x-3\). A point is moving along the curve in such a way that at P the y-coordinate is increasing at 6 units per second.
Find the x-coordinate of P.
Answer/Explanation
Ans:
\(\frac{dy}{dx}=2x-2\)
\(\frac{dy}{dx}=\frac{4}{6}\)
their(2x-2)=their\(\frac{4}{6}\)
\(x=\frac{4}{3}oe\)
Question
The function f is defined by f(x) \(=\frac{1}{3x+2}+x^2\) for x<-1.
Determine whether f is an increasing function, a decreasing function or neither.
Answer/Explanation
Ans:
\(f'(x)=[-(3x+2)^{-2}]\times [3]+[2x]\)
<0 hence decreasing
Question
The gradient of a curve at the point (x,y) is given by \(\frac{dy}{dx} = 2(x+3)^{\frac{1}{2}}-x\). The curve has a stationary point at (a,14), where a is a positive constant.
(a) Find the value of a.
(b) Determine the nature of the stationary point.
(c) Find the equation of the curve.
Answer/Explanation
Ans:
(a) \(2(a+3)^{\frac{1}{2}}-a=0\)
\(4(a+3)=a^2 \rightarrow a^2-4a-12=0\)
\((a-6)(a+2) \rightarrow a=6\)
(b) \(\frac{d^2y}{dx^2}=(x+3)^{-\frac{1}{2}}-1\)
Sub their \(a \rightarrow \frac{d^2y}{dx^2}=\frac{1}{3}-1=-\frac{2}{3}\) (or<0)\(\rightarrow MAX\)
(c) \((y=)\frac{2(x+3)^{-\frac{1}{2}}-1\)
Sub their \(a \rightarrow \frac{d^2y}{dx^2}=\frac{1}{2}x^2(+c)\)
Sub x = their a and y = 14 \(\rightarrow 14 = \frac{4}{3}(9)^{\frac{3}{2}}-18+c\)
\(y=\frac{4}{3}(x+3)^{\frac{3}{2}}-\frac{1}{2}x^2-4\)
Question
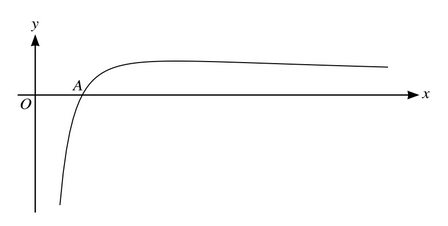
The diagram shows the curve with equation \(y=9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})\). The curve crosses the x-axis at the point A.
(a) Find the x-coordinate of A.
(b) Find the equation of the tangent to the curve at A.
(c) Find the x-coordinate of the maximum point of the curve.
(d) Find the area of the region bounded by the curve, the x-axis and the line x=9.
Answer/Explanation
Ans:
(a) \(9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})=0\) leading to \(9x^{-\frac{3}{2}(x-4)=0\)
x=4 only
(b) \(\frac{dy}{dx}=9(-\frac{1}{2}x^{-\frac{3}{2}}+6x^{-\frac{5}{2}})\)
At x = 4 gradient \(=9(-\frac{1}{16}+\frac{6}{32})=\frac{9}{8}\)
Equation is \(y=\frac{9}{8}(x-4)\)
(c) \(9x^{-\frac{5}{2}}(-\frac{1}{2}x+6)=0\)
x=12
(d) \(\int 9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})dx=9(\frac{x^{\frac{1}{2}}}{\frac{1}{2}}-\frac{4x^{-\frac{1}{2}}}{-\frac{1}{2}})\)
\(9[(6+\frac{8}{3})-(4+4)]\)
6
Question
A curve has equation y = f(x), and it is given that f′ (x) \(= 2x^{2} – 7 – \frac{4}{x^{2}}\)
(a) Given that f(1) = \(-\frac{1}{3}\), find f(x).
(b) Find the coordinates of the stationary points on the curve.
(c) Find f′′ (x).
(d) Hence, or otherwise, determine the nature of each of the stationary points.
Answer/Explanation
(a) \(f(x)=\frac{2}{3}x^{3} – 7x + 4x^{-1}[+c]\)
\(-\frac{1}{3} = \frac{2}{3} – 7 + 4 + c\) leading to c = [2]
\(f(x)=\frac{2}{3}x^{3} – 7x + 4x^{-1} + 2\)
(b) 2x4 – 7x2 – 4 = 0
(2x2 + 1) (x2-4) [=0]
x = [±]
\(\left [ \frac{2}{3}\left ( 2 \right )^{3} -7(2)+\frac{4}{2}+2 leading to\right ] \left ( 2, -\frac{14}{2} \right )\)
\(\left [ \frac{2}{3}\left (-2 \right )^{3} -7(-2)+\frac{4}{-2}+2 leading to\right ] \left ( -2, \frac{26}{3} \right )\)
(c) f” (x) = 4x + 8x-3
(d) f” (2) = 9 > 0 MINIMUM at x = their 2
f”(-2) = -9< 0 MAXIMUM at x = their – 2
Question.
The equation of a curve is \(y =(3 − 2x)^{3} + 24x\).
(a) Find expressions for \(\frac{\partial y}{\partial x}\) and \(\frac{\partial^2 y}{\partial x^2}\).
(b) Find the coordinates of each of the stationary points on the curve.
Answer/Explanation
(a) \(\frac{dx}{dy}=3(3-2x)^{2}x-2+24=-6(3-2x)^{2}+24\)
(B1 without ×−2. B1 for ×−2)
\(\frac{d^{2}y}{dx^{2}}=-12(3-2x)\times -2=24(3-2x)\)
(B1FT from \(\frac{dy}{dx}\) without – 2)
(b) \(\frac{dy}{dx}=0 \ when \ 6(3-2x)^{2}=24\rightarrow 3-2x=\pm 2\)
x = ½, y = 20 or x = 2½, y = 52
(A1 for both x values or a correct pair)
9 (c) If x = ½, \(\frac{d^{2}y}{dx^{2}}=48 \ Minimum\)
If x = 2½, \(\frac{d^{2}y}{dx^{2}}=-48 \ Minimum\)
Question.
The horizontal base of a solid prism is an equilateral triangle of side x cm. The sides of the prism are vertical. The height of the prism is h cm and the volume of the prism is \(2000 cm^3\).
(i) Express h in terms of x and show that the total surface area of the prism, \(Acm^2\) , is given by
\(A=\frac{\sqrt3}{2}x^2+\frac{24000}{\sqrt3}x^{-1}\).
(ii) Given that x can vary, find the value of x for which A has a stationary value.
(iii) Determine, showing all necessary working, the nature of this stationary value.
Answer/Explanation
(i)\(Volume=\left ( \frac{1}{2} \right )x^{2}\frac{\sqrt{3}}{2}h=2000\rightarrow h=\frac{8000}{\sqrt{3}x^{2}}\)\
\(A=3xh+(2)\times \frac{1}{2}\times x^{2}\times \frac{\sqrt{3}}{2}\)
Sub for \(h\rightarrow A=\frac{\sqrt{3}}{2}x^{2}+\frac{24000}{^{\sqrt{3}}}x^{-1}\)
(ii)\(\frac{\mathrm{d} A}{\mathrm{d} x}=\frac{\sqrt{3}}{2}2x-\frac{24000}{\sqrt{3}}x^{-2}\)
=0 when\( x^{3}=8000\rightarrow x=20\)
(iii)\(\frac{\mathrm{d} ^{2}A}{\mathrm{d} x^{2}}=\frac{\sqrt{3}}{2}2+\frac{48000}{\sqrt{3}}x^{-3}> 0\)
→Minimum
Question.
(a) Find the values of the constant m for which the line y = mx is a tangent to the curve \(y = 2x^2 – 4x + 8\).
(b) The function f is defined for x \in R by \(f(x) = x^2 + ax + b\), where a and b are constants. The
solutions of the equation f(x) = 0 are x = 1 and x = 9.
Find
(i) the values of a and b,
(ii) the coordinates of the vertex of the curve y = f(x).
Answer/Explanation
(i)\(y=2x^{2}-4x+8\)
Equates with y=mx and selects a,b,c
Uses \(b^{2}=4ac\)
\(\rightarrow a=-10,b=9\)
(iii) Calculus or \(x=\frac{1}{2}\left ( 1+9 \right )\) by symmetry
\(\rightarrow \left ( 5,-16 \right )\)
Question.

A farmer divides a rectangular piece of land into 8 equal-sized rectangular sheep pens as shown in the diagram. Each sheep pen measures x m by y m and is fully enclosed by metal fencing. The farmer uses 480 m of fencing.
(i) Show that the total area of land used for the sheep pens, \(A m^2\), is given by
\(A = 384x –9.6x^2.\)
(ii) Given that x and y can vary, find the dimensions of each sheep pen for which the value of A is a maximum. (There is no need to verify that the value of A is a maximum.)(
Answer/Explanation
i) \(A=2y\times 4x\left ( =8xy \right )\)
10y+12x=480
\(\rightarrow A=384x-9.6x^{2}\)
(ii)\( \frac{\mathrm{d} A}{\mathrm{d} x}=384-19.2x\)
=0 when x=20
\(\rightarrow x=20,y=24\)
Uses \(x=-\frac{b}{2a}=\frac{-384}{-19.2}=20\),M1,A1
y=24,A1
From graph ,B1 for x=20,M1,A1 for y =24
Question.
A vacuum flask (for keeping drinks hot) is modelled as a closed cylinder in which the internal radius is r cm and the internal height is h cm. The volume of the flask is 1000 cm. A flask is most efficient when the total internal surface area, A \(cm^2\), is a minimum.
(i) Show that \(A =2\Pi r^2+\frac{2000}{r}\).
(ii) Given that r can vary, find the value of r, correct to 1 decimal place, for which A has a stationary value and verify that the flask is most efficient when r takes this value.
Answer/Explanation
Ans:(i) A=2\Pi r(r+h)
\(\Pi r^2 h=1000\rightarrow h=\frac{1000}{\Pi r^{2}}\)
substitute hor h into \(A\rightarrow 2\Pi r^2+\frac{2000}{r}\)
(ii)

Question
The function f is defined by f(x) = 2 − 3 cos x for 0 ≤ x ≤ 20.
(i) State the range of f.
(ii) Sketch the graph of y=f(x).
The function g is defined by g(x)= 2 − 3 cos x for 0 ≤ x ≤ p, where p is a constant.
(iii) State the largest value of p for which g has an inverse.
(iv) For this value of p, find an expression for \(g^{-1}(x)\)
Answer/Explanation
(i)
−1 ⩽ f(x) ⩽ 5 or [–1, 5] (may use y or f instead of f(x))

(iii) (greatest value of p =)π
9(iv)
\(x = 2− 3cosx → cosx =1⁄3(2-x)\)
\(g^{-1}=cos^{-1}\frac{2-x}{3}\)
Question
A curve has equation \(y=x^2-2x-3\). A point is moving along the curve in such a way that at P the y-coordinate is increasing at 6 units per second.
Find the x-coordinate of P.
Answer/Explanation
Ans:
\(\frac{dy}{dx}=2x-2\)
\(\frac{dy}{dx}=\frac{4}{6}\)
their(2x-2)=their\(\frac{4}{6}\)
\(x=\frac{4}{3}oe\)
Question
The function f is defined by f(x) \(=\frac{1}{3x+2}+x^2\) for x<-1.
Determine whether f is an increasing function, a decreasing function or neither.
Answer/Explanation
Ans:
\(f'(x)=[-(3x+2)^{-2}]\times [3]+[2x]\)
<0 hence decreasing
Question
The gradient of a curve at the point (x,y) is given by \(\frac{dy}{dx} = 2(x+3)^{\frac{1}{2}}-x\). The curve has a stationary point at (a,14), where a is a positive constant.
(a) Find the value of a.
(b) Determine the nature of the stationary point.
(c) Find the equation of the curve.
Answer/Explanation
Ans:
(a) \(2(a+3)^{\frac{1}{2}}-a=0\)
\(4(a+3)=a^2 \rightarrow a^2-4a-12=0\)
\((a-6)(a+2) \rightarrow a=6\)
(b) \(\frac{d^2y}{dx^2}=(x+3)^{-\frac{1}{2}}-1\)
Sub their \(a \rightarrow \frac{d^2y}{dx^2}=\frac{1}{3}-1=-\frac{2}{3}\) (or<0)\(\rightarrow MAX\)
(c) \((y=)\frac{2(x+3)^{-\frac{1}{2}}-1\)
Sub their \(a \rightarrow \frac{d^2y}{dx^2}=\frac{1}{2}x^2(+c)\)
Sub x = their a and y = 14 \(\rightarrow 14 = \frac{4}{3}(9)^{\frac{3}{2}}-18+c\)
\(y=\frac{4}{3}(x+3)^{\frac{3}{2}}-\frac{1}{2}x^2-4\)
Question

The diagram shows the curve with equation \(y=9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})\). The curve crosses the x-axis at the point A.
(a) Find the x-coordinate of A.
(b) Find the equation of the tangent to the curve at A.
(c) Find the x-coordinate of the maximum point of the curve.
(d) Find the area of the region bounded by the curve, the x-axis and the line x=9.
Answer/Explanation
Ans:
(a) \(9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})=0\) leading to \(9x^{-\frac{3}{2}(x-4)=0\)
x=4 only
(b) \(\frac{dy}{dx}=9(-\frac{1}{2}x^{-\frac{3}{2}}+6x^{-\frac{5}{2}})\)
At x = 4 gradient \(=9(-\frac{1}{16}+\frac{6}{32})=\frac{9}{8}\)
Equation is \(y=\frac{9}{8}(x-4)\)
(c) \(9x^{-\frac{5}{2}}(-\frac{1}{2}x+6)=0\)
x=12
(d) \(\int 9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})dx=9(\frac{x^{\frac{1}{2}}}{\frac{1}{2}}-\frac{4x^{-\frac{1}{2}}}{-\frac{1}{2}})\)
\(9[(6+\frac{8}{3})-(4+4)]\)
6
Question
A curve has equation y = f(x), and it is given that f′ (x) \(= 2x^{2} – 7 – \frac{4}{x^{2}}\)
(a) Given that f(1) = \(-\frac{1}{3}\), find f(x).
(b) Find the coordinates of the stationary points on the curve.
(c) Find f′′ (x).
(d) Hence, or otherwise, determine the nature of each of the stationary points.
Answer/Explanation
(a) \(f(x)=\frac{2}{3}x^{3} – 7x + 4x^{-1}[+c]\)
\(-\frac{1}{3} = \frac{2}{3} – 7 + 4 + c\) leading to c = [2]
\(f(x)=\frac{2}{3}x^{3} – 7x + 4x^{-1} + 2\)
(b) 2x4 – 7x2 – 4 = 0
(2x2 + 1) (x2-4) [=0]
x = [±]
\(\left [ \frac{2}{3}\left ( 2 \right )^{3} -7(2)+\frac{4}{2}+2 leading to\right ] \left ( 2, -\frac{14}{2} \right )\)
\(\left [ \frac{2}{3}\left (-2 \right )^{3} -7(-2)+\frac{4}{-2}+2 leading to\right ] \left ( -2, \frac{26}{3} \right )\)
(c) f” (x) = 4x + 8x-3
(d) f” (2) = 9 > 0 MINIMUM at x = their 2
f”(-2) = -9< 0 MAXIMUM at x = their – 2
Question.
The equation of a curve is \(y =(3 − 2x)^{3} + 24x\).
(a) Find expressions for \(\frac{\partial y}{\partial x}\) and \(\frac{\partial^2 y}{\partial x^2}\).
(b) Find the coordinates of each of the stationary points on the curve.
Answer/Explanation
(a) \(\frac{dx}{dy}=3(3-2x)^{2}x-2+24=-6(3-2x)^{2}+24\)
(B1 without ×−2. B1 for ×−2)
\(\frac{d^{2}y}{dx^{2}}=-12(3-2x)\times -2=24(3-2x)\)
(B1FT from \(\frac{dy}{dx}\) without – 2)
(b) \(\frac{dy}{dx}=0 \ when \ 6(3-2x)^{2}=24\rightarrow 3-2x=\pm 2\)
x = ½, y = 20 or x = 2½, y = 52
(A1 for both x values or a correct pair)
9 (c) If x = ½, \(\frac{d^{2}y}{dx^{2}}=48 \ Minimum\)
If x = 2½, \(\frac{d^{2}y}{dx^{2}}=-48 \ Minimum\)