Question
A curve has parametric equations.
x = t + ln (t + 1), \(y=3te^{2t}\)
(i) Find the equation of the tangent to the curve at the origin.
(ii) Find the coordinates of the stationary point, giving each coordinate correct to 2 decimal places.
Answer/Explanation
5(i) Use product rule to differentiate y obtaining \(k_{1}e^{2t}+k_{2}te^{2t}\)
Obtain correct \(3e^{2t}+6te^{2t}\)
State derivative of x is \(1+\frac{1}{t+1}\)
Use\( \frac{dy}{dx}=\frac{dy}{dt}/\frac{dx}{dt}\)
with t =0 to find gradient
Obtain\( y=\frac{3}{2}x\) or equivalent
5(ii) Equate\( \frac{dy}{dx} or \frac{dy}{dt}\) to zero and solve for t
Obtain\( t=-\frac{1}{2}\)
Obtain x =−1.19
Obtain y = −0.55
Question
A curve is such that \(\frac{\mathrm{d} y}{\mathrm{d} x}=x^{\frac{1}{2}}-x^{-\frac{1}{2}}\) .The curve passes through the point \(\left ( 4,\frac{2}{3} \right )\)
(i)Find the equation of the curve .
(ii)Find \(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}\)
(iii)Find the coordinates of the stationary point and determine its nature.
Answer/Explanation
(i)\(y=\frac{2}{3}x^{\frac{3}{2}}-2x^{\frac{1}{2}}+c\)
\(\frac{2}{3}=\frac{16}{3}-4+c\)
\(c=-\frac{2}{3}\)
(ii)\(\frac{1}{2}x^{-\frac{1}{2}}+\frac{1}{2}^{-\frac{3}{2}}\)
(iii)\(x^{\frac{1}{2}}-x^{-\frac{1}{2}}=0\)\(\rightarrow \frac{x-1}{\sqrt{x}}=0\)
x=1
When x=1,\(y=\frac{2}{3}-2-\frac{2}{3}=-2\)
When x=1 ,\(\frac{\mathrm{d} ^{2}y}{\mathrm{d} x^{2}}=1> 0\) Hence minimum
Question
(i)Express \(2x^{2}-12x+13\) in the form \(a\left ( x+b \right )^{2}+c\) where a,b and c are constants.
(ii)The function f is defined by \(f\left ( x \right )=2x^{2}-12x+13 \) for \( x\geq k\) where k is a constant.It is given that f is a one-one function.State the smallest possible value of k.
The value of k is now given to be 7.
(iii) Find the range of f.
(iv) Find an expression for \(f^{-1}\left ( x \right )\) and state the domain of \(f^{-1}\).
Answer/Explanation
(i) \(2\left ( x-3 \right )^{2}-5\) or a=2,b=-3,c=-5
(ii) 3
(iii)\(\left ( y \right )\geq 27\)
(iv)\(2\left ( x-3 \right )^{2}=\left ( y+5 \right )\)
\(x-3=\left ( \pm \right )\sqrt{\frac{1}{2}\left ( y+5 \right )}\)
\(x=3+\left ( \pm \right )\sqrt{\frac{1}{2}\left ( y+5 \right )}\)
\(\left ( f^{-1}\left ( x \right ) \right )=3+\sqrt{\frac{1}{2}\left ( x+5 \right )}\) for \(x\geq 27\)
Question
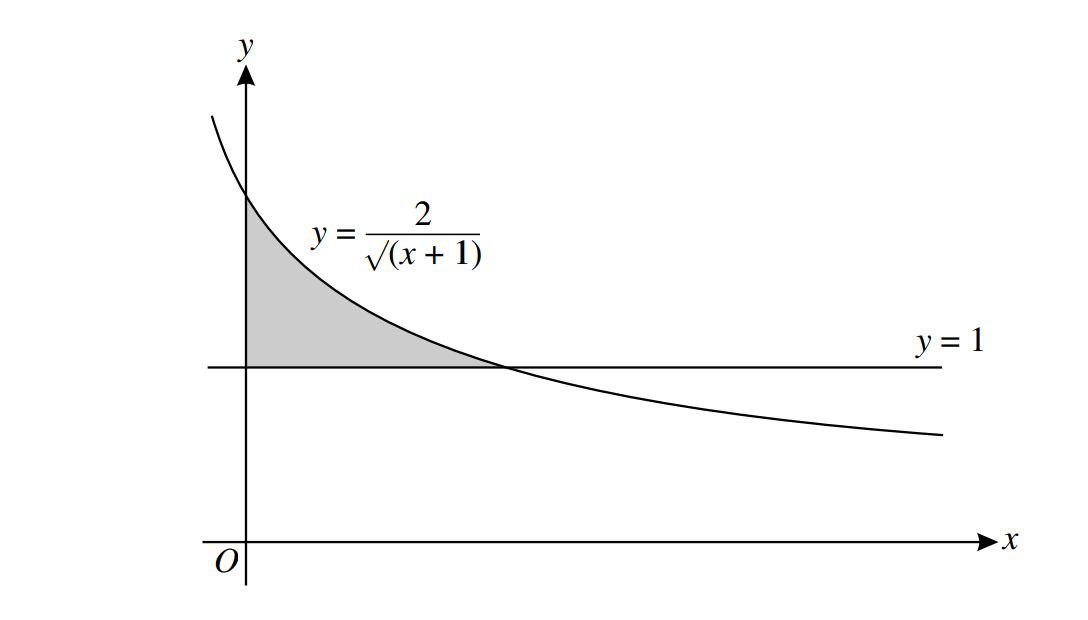
The diagram shows the line y=1 and the part of the curve \(y=\frac{2}{\sqrt{\left ( x+1 \right )}}\).
(i)Show that the equation \(y=\frac{2}{\sqrt{\left ( x+1 \right )}}\) can be written in the form \(x=\frac{4}{y^{2}}-1\)
(ii)Find \(\int \left ( \frac{4}{y^{2}}-1 \right )dy\).Hence find the area of the shaded region.
(ii)The shaded region is rotated through about the y-axis.Find the exact value of the volume of revolution obtained.
Answer/Explanation
(i) \(x=\frac{4}{y^{2}}-1\)
(ii)\(\int \left ( \frac{4}{y^{2}}-1 \right )dy=\left [- \frac{4}{y} -y\right ]\)
\(^{2}_{1}\left [ -\frac{4}{2}-2-\left ( -4-1 \right ) \right ]\)
(iii)\(\pi \int x^{2}dy=\left ( \pi \right )\int \left ( \frac{16}{y^{4}}-\frac{8}{y^{2}} +y\right )\)
\(\left ( \pi \right )\left [ -\frac{16}{3y^{3}}+\frac{8}{y} +y\right ]\)
\(\left ( \pi \right )\left [\left ( -\frac{16}{24}+4+2 \right )-\left ( -\frac{-16}{3}+8+1\right )\right ]\)
\(\frac{5\pi }{3}\)
Question
A curve has equation \(y=f(x)\) and it is given that \(f{}'(x)=3x^{\frac{1}{2}}-2x^{-\frac{1}{2}}\),The point A is the onl;y point in the curve at which gradient is -1
(i)Find the x-coordinate of A.
(ii)Given that curve also passes through the point (4,10),find the coordinate of A, giving your answer as a fraction.
Answer/Explanation
(i) \(3z-\frac{2}{z}=-1\Rightarrow 3z^{2}+z-2=0\0
\(x^{\frac{1}{2}}(or z)\) \(=\frac{2}{3}\) or -1
\(x=\frac{4}{9}\) only
(ii)\(f(x)=\frac{3x^{\frac{3}{2}}}{\frac{3}{2}}-\frac{2x^{\frac{1}{2}}}{\frac{1}{2}}\)(+c)
Sub x=4,y=10 \(10=16-8+c\Rightarrow c=2\)
When \(x=\frac{4}{9}\),\(y=2\left ( \frac{4}{9} \right )^{\frac{3}{2}}-4\left ( \frac{4}{9} \right )^{\frac{1}{2}}+2\)
\(-\frac{2}{27}\)
Question
A curve is such that \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{8}{x^{3}}-1\) and the point (2,4)lies on the curve.Find the equation of the curve.
Answer/Explanation
\(y=\frac{4}{x^{2}}-x\)
Sub(2,4)\(\rightarrow c=5\)
Question
A curve has equation \(y=f(x)\) . It is given that \(f{}’\left ( x \right )=\frac{1}{\sqrt{x+6}}+\frac{6}{x^{2}}\) and that \(f(3)=1\) . Find f(x).
Answer/Explanation
Attempt integration
\(f(x)=2(x+6)^{\frac{1}{2}}-\frac{6}{x}\)
\(2(3)-\frac{6}{3}+c=1\)
c=-3
Question
The function f is defined for x > 0 and is such that \( f{}’\left ( x \right )=2x-\frac{2}{x^{2}}\). The curve y = f(x) passes through the point P(2, 6.)
(i) Find the equation of the normal to the curve at P.
(ii) Find the equation of the curve.
(iii) Find the x-coordinate of the stationary point and state with a reason whether this point is a maximum or a minimum.
Answer/Explanation
(i)\(f{}'(2)=4-\frac{1}{2}=\frac{7}{2}\rightarrow \)gradient of normal =\(-\frac{2}{7}\)
\(y-6=-\frac{2}{7}(x-2)\)
(ii)\(f(x)=x^{2}+\frac{2}{x}+c\)
6=4+1+c⇒c=1
(iii)\(2x-\frac{2}{x^{2}}=0\)⇒\(2x^{3}-2=0\)
x=1
\(f{}”(x)=2+\frac{4}{x^{3}}\) or any valid method
\(f{}”(1)=6\) >0 hence minimum\)
Question
A curve for which \( \frac{\mathrm{d} y}{\mathrm{d} x}=7-x^{2}-6x \) pases tghrough the p[oint (3,-10)
(i)Find the equation of the curve.
(ii)Express \(7-x^{2}-6x\) in the form \(a-(x+b)^{2}\),where a and b are constants.
(iii)Find the set of values of x for which the gradient of the curve is positive.
Answer/Explanation
(i)\(y=7x-\frac{x^{3}}{3}-\frac{6x^{2}}{2}+c\)
Uses (3,-10) →c=5
(ii)\(7-x^{2}-6x=16-(x+3)^{2}\)
(iii)\(16-\left ( x+3 \right )^{2}> 0\rightarrow \left ( x+3 \right )^{2}< 16\),and solve
End-points x=1 or -7
\(\rightarrow -7< x< 1\)
Question.
A curve is such that \(\frac{\partial y}{\partial x}==2-8(3x+4)^\frac{1}{2}\)
(i) A point P moves along the curve in such a way that the x-coordinate is increasing at a constant rate of 0.3 units per second.
Find the rate of change of the y-coordinate as P crosses the y-axis.
The curve intersects the y-axis where y =\frac{4}{3}
(ii) Find the equation of the curve.
Answer/Explanation
(i) \(\frac{\mathrm{d} y}{\mathrm{d} x}=2-8\left ( 3x+4 \right )^{-\frac{1}{2}}\)
\(\left ( x=0,\rightarrow \frac{\mathrm{d} y}{\mathrm{d} x} =-2\right )\)
\(\frac{\mathrm{d} y}{\mathrm{d} t}=\frac{\mathrm{d} y}{\mathrm{d} x}\times \frac{\mathrm{d} x}{\mathrm{d} t}\rightarrow -0.6\)
(ii) \(y=\left \{ 2x \right \}\left \{ -\frac{8\sqrt{3x+4}}{\frac{1}{2}}\div 3 \right \}\left ( +c \right )\)
\(x=0,y=\frac{4}{3}\rightarrow c=12\)
Question.
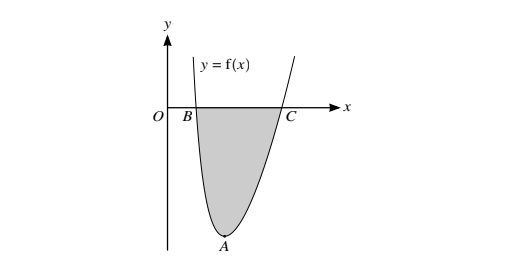
The diagram shows the curve \(y = f(x).\) defined for x > 0. The curve has a minimum point at A and
crosses the x-axis at B and C. It is given that \(\frac{\partial y}{\partial x}=2x-\frac{2}{x^3}\) and that the curve passes through the point \((4,\frac{189}{6})\)
(i) Find the x-coordinate of A
(ii) Find f(x).
(iii) Find the x-coordinates of B and C.
(iv) Find, showing all necessary working, the area of the shaded region.
Answer/Explanation
(i) \(\frac{2x-2}{x^{3}}=0\)
\(x^{4}=1\Rightarrow x=1\) at A cao
(ii)\(f\left ( x \right )=\frac{x^{2}+1}{x^{2}}\left ( +c \right )\) cao
\(\frac{189}{16}=\frac{16+1}{16+c}\)
\(c=-\frac{17}{4}\)
(iii) \(\frac{x^{2}+1}{x^{2}-\frac{17}{4}}=0\Rightarrow 4x^{4}-17x^{2}+4\left ( =0 \right )\)
\(\left ( 4x^{2} -1\right )\left ( x^{2}-4 \right )\left ( =0 \right )\)
\(x=\frac{1}{2},2\)
(iv)\( \int \left (\frac{ x^{2}+x^{-2}-17 }{4}\right )dx=\frac{x^{3}}{3}-\frac{1}{x}-\frac{17x}{4}\)
\(\left ( \frac{8}{3}-\frac{1}{2}-\frac{17}{2} \right )-\left ( \frac{1}{24}-2-\frac{17}{8} \right )\)
\(Area=\frac{9}{4}\)
Question
The function f is defined by f(x) = 2 − 3 cos x for 0 ≤ x ≤ 20.
(i) State the range of f.
(ii) Sketch the graph of y=f(x).
The function g is defined by g(x)= 2 − 3 cos x for 0 ≤ x ≤ p, where p is a constant.
(iii) State the largest value of p for which g has an inverse.
(iv) For this value of p, find an expression for \(g^{-1}(x)\)
Answer/Explanation
(i)
−1 ⩽ f(x) ⩽ 5 or [–1, 5] (may use y or f instead of f(x))
(iii) (greatest value of p =)π
9(iv)
\(x = 2− 3cosx → cosx =1⁄3(2-x)\)
\(g^{-1}=cos^{-1}\frac{2-x}{3}\)
Question
The function f is defined by f(x) = 2 − 3 cos x for 0 ≤ x ≤ 20.
(i) State the range of f.
(ii) Sketch the graph of y=f(x).
The function g is defined by g(x)= 2 − 3 cos x for 0 ≤ x ≤ p, where p is a constant.
(iii) State the largest value of p for which g has an inverse.
(iv) For this value of p, find an expression for \(g^{-1}(x)\)
Answer/Explanation
(i)
−1 ⩽ f(x) ⩽ 5 or [–1, 5] (may use y or f instead of f(x))

(iii) (greatest value of p =)π
9(iv)
\(x = 2− 3cosx → cosx =1⁄3(2-x)\)
\(g^{-1}=cos^{-1}\frac{2-x}{3}\)
Question
A curve with equation y = f(x) passes through the points ( 0, 2) and (3, −1 ) It is given that \({f}'(x)=kx^{2}-2x\) , where k is a constant. Find the value of k.
Answer/Explanation
\(y=\frac{1}{3}kx^{3}-x^{2}+(c)\) Sub (0, 2) Sub (3,‒1)→ \(−1= 9k-9 + their c\)
\(k=\frac{2}{3}\)
Question
The equation of a curve is such that \(\frac{dy}{dx}=\frac{1}{(x-3)^{2}}+x\). . It is given that the curve passes through the
point (2, 7).
Find the equation of the curve. [4]
Answer/Explanation
Ans
2 \((y=)\left [ -(x-3)^{-1} \right ]\left [ +\frac{1}{2}x^{2} \right ](+c)\)
7 = 1 + 2 + c
\(y=-(x-3)^{-1}+\frac{1}{2}x^{2}+4\)
Question
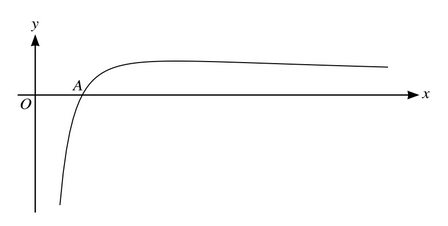
The diagram shows the curve with equation \(y=9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})\). The curve crosses the x-axis at the point A.
(a) Find the x-coordinate of A.
(b) Find the equation of the tangent to the curve at A.
(c) Find the x-coordinate of the maximum point of the curve.
(d) Find the area of the region bounded by the curve, the x-axis and the line x=9.
Answer/Explanation
Ans:
(a) \(9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})=0\) leading to \(9x^{-\frac{3}{2}(x-4)=0\)
x=4 only
(b) \(\frac{dy}{dx}=9(-\frac{1}{2}x^{-\frac{3}{2}}+6x^{-\frac{5}{2}})\)
At x = 4 gradient \(=9(-\frac{1}{16}+\frac{6}{32})=\frac{9}{8}\)
Equation is \(y=\frac{9}{8}(x-4)\)
(c) \(9x^{-\frac{5}{2}}(-\frac{1}{2}x+6)=0\)
x=12
(d) \(\int 9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})dx=9(\frac{x^{\frac{1}{2}}}{\frac{1}{2}}-\frac{4x^{-\frac{1}{2}}}{-\frac{1}{2}})\)
\(9[(6+\frac{8}{3})-(4+4)]\)
6
Question
The equation of a curve is such that \(\frac{dx}{dy}=\frac{3}{x^{4}}+32x^{3}\).
It is given that the curve passes through the point \(\left ( \frac{1}{2},4 \right )\)
Find the equation of the curve.
Answer/Explanation
Ans
1 \([y=]-\frac{1}{x^{3}}+8x^{4}[+c]\)
\(4=-8+\frac{1}{2}+c\)
\(y=-\frac{1}{x^{3}}+8x^{4}+\frac{23}{2}\)